Производная и дифференциал
Геометрические изложения и дифференцированные исчисления (построение графиков)
Исследуем функцию на возрастание, убывание и экстремум. Для этого найдем производную функции
Неопределенный интеграл
Результат интегрирования проверим дифференцированием. Для этого найдем производную
Функции нескольких переменных, дифференцированных исчислений
Навигация
Неопределенный интеграл
Пределы последовательностей и функций
18636
знаков
4
таблицы
6
изображений
4. Неопределенный интеграл
Часто возникает задача, обратная той, которая решалась в дифференциальном исчислении, а именно: дана функция 
, найти функцию 
, такую, что 
.
Функция называется первообразной для данной функции на некотором промежутке Х, если для любого 
выполняется равенство
.
Например, пусть 
, тогда за первообразную можно взять 
, поскольку 
.
В основе интегрального исчисления лежит теорема об общем виде первообразной: если – первообразная для функции на промежутке Х, то все первообразные для функции имеют вид 
, где С – произвольная постоянная.
Выражение вида описывает все первообразные для функции 
. Действительно, для любой постоянной С
.
Пусть наряду с данной первообразной функция 
– также первообразная для . Тогда должны выполняться равенства
,
откуда 
. Следовательно, разность этих первообразных будет тождественно равна константе 
или 
.
Действие нахождения первообразной называется интегрированием функции.
Доказанная теорема позволяет ввести основное понятие интегрального исчисления: если – первообразная для , то совокупность функций , где С – произвольная постоянная, называется неопределенным интегралом от функции , который обозначается следующим образом
.
Геометрически неопределенный интеграл представляет собой семейство плоских кривых 
, называемых интегральными.
Для того, чтобы проверить, правильно ли выполнено интегрирование, надо взять производную от результата и убедиться, что получена подынтегральная функция . Как всякая обратная операция, интегрирование – более сложное действие, чем дифференцирование.
Приведем основные свойства неопределенного интеграла:
1. производная неопределенного интеграла равна подынтегральной функции
;
2. неопределенный интеграл от алгебраической суммы функций равен сумме интегралов от слагаемых функций
;
3. постоянный множитель можно выносить за знак неопределенного интеграла
.
Значения интегралов от основных элементарных функций получаются из формул дифференцирования этих функций. Приведем таблицу основных интегралов:
| 1) | 7) |
| 2) | 8) |
| 3) | 9) |
| 4) | 10) |
| 5) | 11) |
| 6) | 12) |
;
;
;
;
;
;
;
;
;
;
.Интегралы, содержащиеся в этой таблице, называются табличными.
Пример. Найти неопределенный интеграл. Результат интегрирования проверить дифференцированием
Решение: Для нахождения неопределенных интегралов можно воспользоваться как методом замены переменной, так и методом внесения под знак дифференциала. Покажем оба метода.
1. Воспользуемся методом замены переменной. Введем новую переменную t по формуле 
. Тогда 
или 
. Тогда
После замены переменной воспользовались свойством неопределенного интеграла: постоянный множитель 
можно выносить за знак неопределенного интеграла, и так как 
, то пришли к табличному интегралу 
, где 
и 
.
2. Решим этот пример методом внесения под знак дифференциала. Замечая, что 
и то, что подынтегральное выражение можно представить в виде
,
внесем под знак дифференциала 
. Для этого выпишем дифференциал этой функции 
. Тогда
После внесения под знак дифференциала функции пришли к табличному интегралу , где и 
.
Похожие работы
... знаменателя и отношению коэффициентов при старших членах, если степени числителя и знаменателя равны. Для упрощения задачи нахождения предела последовательности, вышеуказанного вида, мы прибегаем к помощи теоремы Штольца. Теорема Штольца Для определения пределов неопределённых выражений типа часто бывает полезна следующая теорема, принадлежащая Штольцу (O. Stolz). Теорема: Пусть варианта , ...
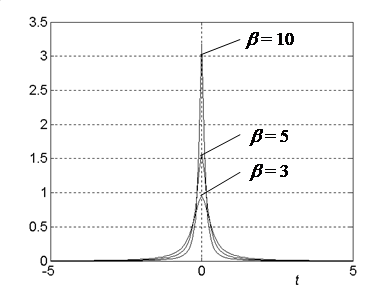
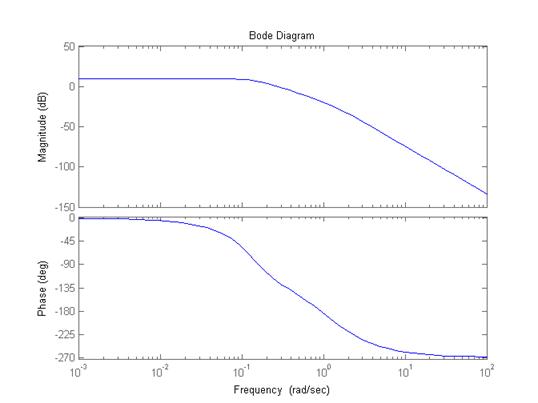
... такому произведению будет соответствовать свертка. Другими словами, выходной процесс системы, на которую действуют управляющее и возмущающее воздействия со своими передаточными функциями и , в действительной области можно представить в виде , . 5 Графические представления частотных характеристик Как уже отмечалось, частотные представления являются основой классических методов теории ...
... предел функции: Решение. Воспользуемся первым замечательным пределом Тогда Пример 3. Найти предел функции: Решение. Воспользуемся вторым замечательным пределом Тогда Непрерывность функции нескольких переменных По определению функция f (x, y) непрерывна в точке (х0, у0), если она определена в некоторой ее окрестности, в том числе в самой точке (х0, у0) и если предел f (x, y) в этой ...
... производной: diff (f (х) , х$3). Пример 1. Вычисление производных. > s:=x^3*cos(x)+y^2*ln(sin(x)); > diff(s,x); > diff(s,x$2); > diff(s,x,y); > fs:=Diff(s,x); > q:=sqrt(fs); > value(%); Последние три команды показывают использование отложенной формы команды дифференцирования. 2. Интегрирование выражений Команда int( ) имеет отложенную форму ...
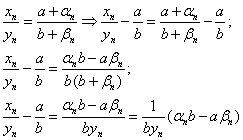
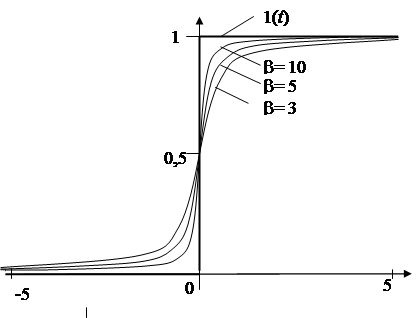
0 комментариев