Производная и дифференциал
Геометрические изложения и дифференцированные исчисления (построение графиков)
Исследуем функцию на возрастание, убывание и экстремум. Для этого найдем производную функции
Неопределенный интеграл
Результат интегрирования проверим дифференцированием. Для этого найдем производную
Функции нескольких переменных, дифференцированных исчислений
Навигация
Результат интегрирования проверим дифференцированием. Для этого найдем производную
Пределы последовательностей и функций
18636
знаков
4
таблицы
6
изображений
3. Результат интегрирования проверим дифференцированием. Для этого найдем производную
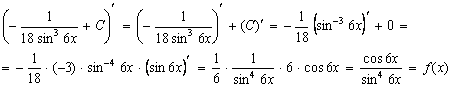
Таким образом, производная от неопределенного интеграла равна подынтегральной функции, следовательно, интеграл от данной функции найден, верно.
5. Определенный интеграл
Определение определенного интеграла. Пусть функция 
задана на отрезке [а, b]. Разобьем отрезок [а, b] на п произвольных частей точками
.
Точки, разделяющие отрезок [а, b] на частичные отрезки 
длиной 
, называются точками разбиения. Внутри каждого частичного отрезка выберем произвольную точку 
. Образуем сумму произведений
,
называемую интегральной суммой для функции на отрезке [а, b]. Геометрический смысл величины s показан на рис. 2.. Это сумма площадей прямоугольников с основаниями 
и высотами 
.
При этом числа a и b называются соответственно нижним и верхним пределами, выражение 
– подынтегральным выражением, – подынтегральной функцией.
Определенный интеграл численно равен площади криволинейной трапеции, ограниченной вертикальными прямыми 
при 
, осью Ох и графиком неотрицательной и непрерывной функции 
. В этом состоит его геометрический смысл.
Если предположить, что 
– производительность труда в момент t, то 
будет численно равен объему произведенной продукции за промежуток 
, т. е. определенному интегралу можно придать экономический смысл.
| у
Мi
mi А О х0=а хi Рис. 2 | Предел интегральной суммы
|
хi+1 b= хn х
при стремлении 
к нулю, не зависящий от способа выбора точек 
и точек 
, называется определенным интегралом от функции 
Определенный интеграл обладает рядом свойств, аналогичных свойствам неопределенного интеграла:
1) постоянный множитель можно выносить за знак интеграла;
2) интеграл от алгебраической суммы функций равен такой же сумме интегралов от этих функций (свойство линейности).
Кроме того, определенному интегралу присущи свойства, не имеющие аналогов в теории неопределенных интегралов:
3) интеграл от постоянной величины равен этой постоянной, умноженной на длину отрезка интегрирования
;
4) при перемене местами пределов интегрирования интеграл изменяет лишь знак
;
5) интеграл с одинаковыми пределами интегрирования равен нулю
;
6) для любых чисел а, b и c имеет место равенство
.
Пример. Вычислить определенный интеграл с точностью до двух знаков после запятой
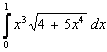
Решение:
Воспользуемся методом замены переменной. Введем новую переменную t по формуле 
. Тогда 
или 
. Осуществим пересчет пределов интегрирования, используя вид замены. Подставим нижний предел интегрирования старой переменной 
в выражение и найдем нижний предел интегрирования новой переменной 
. Аналогично, подставляя верхний предел интегрирования старой переменной 
, найдем верхний предел интегрирования новой переменной 
. Тогда
Похожие работы
... знаменателя и отношению коэффициентов при старших членах, если степени числителя и знаменателя равны. Для упрощения задачи нахождения предела последовательности, вышеуказанного вида, мы прибегаем к помощи теоремы Штольца. Теорема Штольца Для определения пределов неопределённых выражений типа часто бывает полезна следующая теорема, принадлежащая Штольцу (O. Stolz). Теорема: Пусть варианта , ...
... такому произведению будет соответствовать свертка. Другими словами, выходной процесс системы, на которую действуют управляющее и возмущающее воздействия со своими передаточными функциями и , в действительной области можно представить в виде , . 5 Графические представления частотных характеристик Как уже отмечалось, частотные представления являются основой классических методов теории ...
... предел функции: Решение. Воспользуемся первым замечательным пределом Тогда Пример 3. Найти предел функции: Решение. Воспользуемся вторым замечательным пределом Тогда Непрерывность функции нескольких переменных По определению функция f (x, y) непрерывна в точке (х0, у0), если она определена в некоторой ее окрестности, в том числе в самой точке (х0, у0) и если предел f (x, y) в этой ...
... производной: diff (f (х) , х$3). Пример 1. Вычисление производных. > s:=x^3*cos(x)+y^2*ln(sin(x)); > diff(s,x); > diff(s,x$2); > diff(s,x,y); > fs:=Diff(s,x); > q:=sqrt(fs); > value(%); Последние три команды показывают использование отложенной формы команды дифференцирования. 2. Интегрирование выражений Команда int( ) имеет отложенную форму ...
0 комментариев