Производная и дифференциал
Геометрические изложения и дифференцированные исчисления (построение графиков)
Исследуем функцию на возрастание, убывание и экстремум. Для этого найдем производную функции
Неопределенный интеграл
Результат интегрирования проверим дифференцированием. Для этого найдем производную
Функции нескольких переменных, дифференцированных исчислений
Навигация
Исследуем функцию на возрастание, убывание и экстремум. Для этого найдем производную функции
Пределы последовательностей и функций
18636
знаков
4
таблицы
6
изображений
6. Исследуем функцию на возрастание, убывание и экстремум. Для этого найдем производную функции.
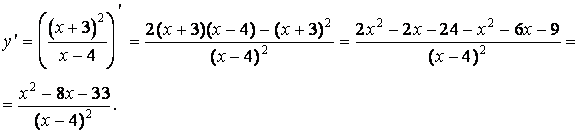
Из 
получаем 
, откуда 
, 
.
+ _ +
______________________________________ x
-3 11
Так как на интервалах 
и 
производная положительна, т.е. 
, то график функции на указанных интервалах возрастает. Так как на интервале 
производная отрицательна, т.е. 
, то на указанном интервале график функции убывает.
Так как при переходе через точки , производная функции меняет знаки и эти точки входят в область определения функции, то , - точки локального экстремума. Причем точка локального минимума: 
(так как при переходе через нее производная меняет знак с "+" на "-"); - точка локального максимума: 
(так как при переходе через нее производная меняет знак с "-" на "+").
7. Исследуем график функции на выпуклость, вогнутость и определим точки перегиба. Для этого найдем вторую производную функции.
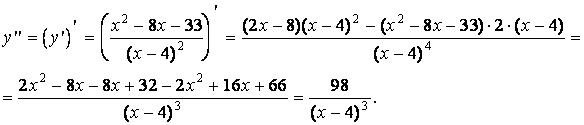
Очевидно, что в интервале 
вторая производная меньше нуля, т.е. 
, и в этом интервале график функции является выпуклым вверх. В интервале 
вторая производная больше нуля, т.е. 
, и в этом интервале график функции является выпуклым вниз (вогнутым).
Несмотря на то, что при переходе через точку 
вторая производная меняет знак, она не является точкой перегиба, так как не входит в область определения функции, т.е. функция в ней не определена. Таким образом, точек перегиба у графика функции нет.
Из получаем , откуда , .
+ _ +
______________________________________ x
-3 11
Так как на интервалах и производная положительна, т.е. , то график функции на указанных интервалах возрастает. Так как на интервале производная отрицательна, т.е. , то на указанном интервале график функции убывает.
Так как при переходе через точки , производная функции меняет знаки и эти точки входят в область определения функции, то , - точки локального экстремума. Причем точка локального минимума: (так как при переходе через нее производная меняет знак с "+" на "-"); - точка локального максимума: (так как при переходе через нее производная меняет знак с "-" на "+").
Похожие работы
... знаменателя и отношению коэффициентов при старших членах, если степени числителя и знаменателя равны. Для упрощения задачи нахождения предела последовательности, вышеуказанного вида, мы прибегаем к помощи теоремы Штольца. Теорема Штольца Для определения пределов неопределённых выражений типа часто бывает полезна следующая теорема, принадлежащая Штольцу (O. Stolz). Теорема: Пусть варианта , ...
... такому произведению будет соответствовать свертка. Другими словами, выходной процесс системы, на которую действуют управляющее и возмущающее воздействия со своими передаточными функциями и , в действительной области можно представить в виде , . 5 Графические представления частотных характеристик Как уже отмечалось, частотные представления являются основой классических методов теории ...
... предел функции: Решение. Воспользуемся первым замечательным пределом Тогда Пример 3. Найти предел функции: Решение. Воспользуемся вторым замечательным пределом Тогда Непрерывность функции нескольких переменных По определению функция f (x, y) непрерывна в точке (х0, у0), если она определена в некоторой ее окрестности, в том числе в самой точке (х0, у0) и если предел f (x, y) в этой ...
... производной: diff (f (х) , х$3). Пример 1. Вычисление производных. > s:=x^3*cos(x)+y^2*ln(sin(x)); > diff(s,x); > diff(s,x$2); > diff(s,x,y); > fs:=Diff(s,x); > q:=sqrt(fs); > value(%); Последние три команды показывают использование отложенной формы команды дифференцирования. 2. Интегрирование выражений Команда int( ) имеет отложенную форму ...
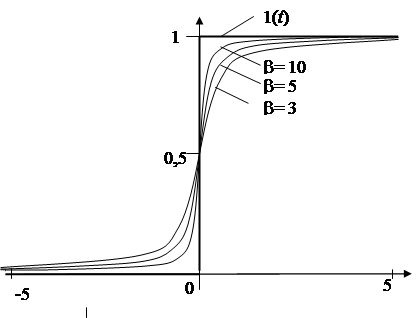
0 комментариев