Производная и дифференциал
Геометрические изложения и дифференцированные исчисления (построение графиков)
Исследуем функцию на возрастание, убывание и экстремум. Для этого найдем производную функции
Неопределенный интеграл
Результат интегрирования проверим дифференцированием. Для этого найдем производную
Функции нескольких переменных, дифференцированных исчислений
Навигация
Геометрические изложения и дифференцированные исчисления (построение графиков)
Пределы последовательностей и функций
18636
знаков
4
таблицы
6
изображений
3 Геометрические изложения и дифференцированные исчисления (построение графиков)
Функция 
, определенная во всех точках промежутка 
, называется возрастающей (убывающей) в этом промежутке, если для любых двух значений аргумента, принадлежащих этому промежутку, большему из них соответствует большее (меньшее) значение функции, т. е,
если 
то при
– возрастающая, 
– убывающая.
Из данного определения вытекает, что для возрастающей функции приращения аргумента и функции имеет один и тот же знак, в силу чего их отношение положительно: 
. Для убывающей функции эти приращения имеют разные знаки, в силу чего 
. Те значения аргумента, при которых функция достигает своих наибольших и наименьших по сравнению с близкими значений, называются точками максимума и минимума (точками экстремума).
Точка 
называется точкой максимума (минимума) непрерывной функции 
, а значение 
называется максимумом (минимумом) этой функции, если существует некоторая окрестность точки 
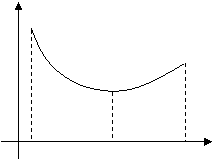
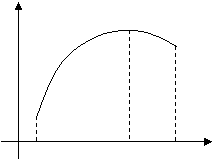
такая, что значение функции в любой точке этой окрестности будет меньше (больше), чем ее значение в самой точке , т. е. меньше (больше), чем максимум (минимум) (рис. 1).
у max у
min
f(х0) f(х0)
О х0–d х0 х0+d х О х0–d х0 х0+d х
| точка максимума | точка минимума |
Рис. 1
Из определений точек экстремума следует, что вне d-окрестности точки экстремума поведение функции произвольно, т. е. понятия максимума и минимума функции носят характер локальных (местных), а не абсолютных понятий.
Чтобы установить признаки возрастания и убывания и признаки экстремума функций, рассмотрим ряд важных теорем математического анализа, на которые опираются все дальнейшие исследования функций.
Рекомендуется исследование функций проводить в определенной последовательности.
1. Найти область определения функции; точки разрыва и их характер; вертикальные асимптоты графика.
2. Определить возможный тип симметрии функции (четность, нечетность функции); точки пересечения графика функции с осями координат, т. е. решить уравнения 
и 
.
4. Использовать первую производную для определения области возрастания и убывания и экстремумов функции.
5. Использовать вторую производную для определения участков выпуклости и вогнутости графика и точек перегиба.
6. Построить график функции с учетом проведенного исследования.
Пример. Провести полное исследование функции
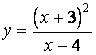
Решение:
Проведем полное исследование функции, используя следующую схему:
найти область определения функции;
исследовать на четность и нечетность функцию;
найти точки разрыва функции;
найти асимптоты (вертикальные, наклонные и горизонтальные) графика функции;
найти точки пересечения графика функции с координатными осями;
исследовать функцию на монотонность (указав интервалы возрастания и убывания) и экстремум;
определить интервалы выпуклости и вогнутости графика функции, точки перегиба;
при необходимости вычислить значения функции в дополнительных точках;
построить схематично график функции, используя результаты полученные в пунктах 1-8.
Областью определения функции является множество 
.
Так как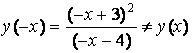 
и 
, то функция не является ни четной, ни нечетной.
Функция претерпевает разрыв в точке 
.
Найдем асимптоты графиков функции:
а). Прямая является вертикальной асимптотой, т.к.
, 
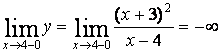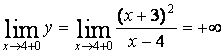
б). Находим наклонные и горизонтальные асимптоты (горизонтальные асимптоты являются частным случаем наклонных асимптот) 
,
где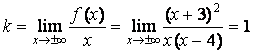 
;
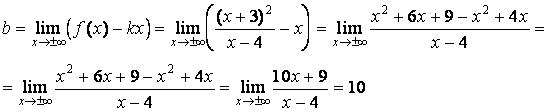
Таким образом, прямая 
является единственной наклонной асимптотой и на 
, и на 
.
Найдем точки пересечения графика функции с осями координат.
а) С осью 
: 
, 
, т.е. точка пересечения с осью - 
.
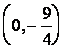б) С осью 
: 
, 
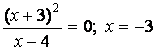, т.е. точка пересечения с осью - 
.
Похожие работы
... знаменателя и отношению коэффициентов при старших членах, если степени числителя и знаменателя равны. Для упрощения задачи нахождения предела последовательности, вышеуказанного вида, мы прибегаем к помощи теоремы Штольца. Теорема Штольца Для определения пределов неопределённых выражений типа часто бывает полезна следующая теорема, принадлежащая Штольцу (O. Stolz). Теорема: Пусть варианта , ...
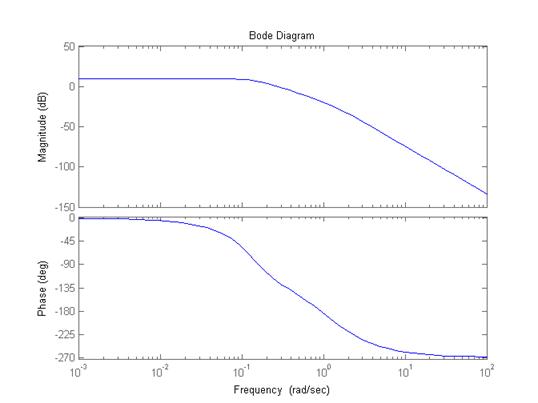
... такому произведению будет соответствовать свертка. Другими словами, выходной процесс системы, на которую действуют управляющее и возмущающее воздействия со своими передаточными функциями и , в действительной области можно представить в виде , . 5 Графические представления частотных характеристик Как уже отмечалось, частотные представления являются основой классических методов теории ...
... предел функции: Решение. Воспользуемся первым замечательным пределом Тогда Пример 3. Найти предел функции: Решение. Воспользуемся вторым замечательным пределом Тогда Непрерывность функции нескольких переменных По определению функция f (x, y) непрерывна в точке (х0, у0), если она определена в некоторой ее окрестности, в том числе в самой точке (х0, у0) и если предел f (x, y) в этой ...
... производной: diff (f (х) , х$3). Пример 1. Вычисление производных. > s:=x^3*cos(x)+y^2*ln(sin(x)); > diff(s,x); > diff(s,x$2); > diff(s,x,y); > fs:=Diff(s,x); > q:=sqrt(fs); > value(%); Последние три команды показывают использование отложенной формы команды дифференцирования. 2. Интегрирование выражений Команда int( ) имеет отложенную форму ...
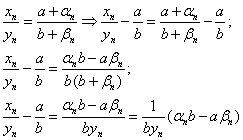
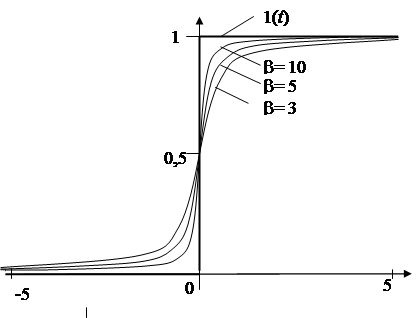
0 комментариев