Навигация
Результати програмної реалізації мультиплексорів, демультиплексорів, шифраторів, дешифраторів
7.4.6 Результати програмної реалізації мультиплексорів, демультиплексорів, шифраторів, дешифраторів
На рис. 7.4.7 зображено вікно сигнального редактору проекту “shifrator1”.
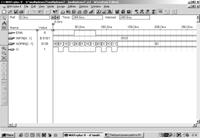
Рис.7.4.7. Результати тестування шифратора 10 на 4
На рис. 7.4.8 зображено вікно сигнального редактору проекту “decipherer1”.

Рис. 7.4.8. Результати тестування повного 3-розрядного дешифратора з інверсними виходами
На рис. 7.4.9 зображено вікно сигнального редактору проекту “multiplexer2”.
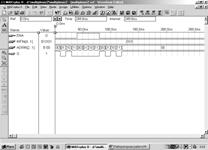
Рис. 7.4.9. Результати тестування мультиплексора з 2 адресними входами, 4 інформаційними і входом дозволу роботи
На рис. 7.4.10 зображено вікно сигнального редактору проекту “demultiplexer1”.
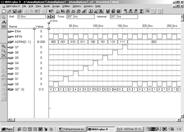
Рис. 7.4.10. Результати тестування демультиплексора з 3 адресними входами,1 інформаційним і входом дозволу роботи
7.5 Теоретичні відомості про суматори, віднімані
7.5.1 Суматори
Крайній лівий розряд двійкового числа, такого, наприклад, як 101011, називають самим старшим розрядом (ССР), а крайній правий розряд – самим молодшим розрядом (СМР). Нагадаємо, що розряди представленого двійкового числа в порядку зростання старшинства мають ваги (зправа налiво) 1, 2, 4, 8, 16, 32.
Оскільки в двійкових числах присутні лише дві цифри (0 і 1), таблиця додавання досить проста. Вона приведена на рис. 7.5.1. Як і в випадку додавання десяткових чисел, три перших результати не викликають питань. Що стосується останньої задачі (1+1), то при складанні десяткових чисел в даному випадку відповіддю було б число 2. Таким чином, при двійковому додаванні 1+1=0 плюс перенос 1 в сусідній старший двійковий розряд.
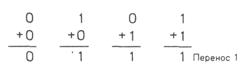
Рис. 7.5.1. Таблиця двійкового додавання
Ще один приклад на складання двійкових чисел представлено на рис. 7.5.2,а.
|
|
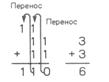
 Рис. 7.5.2. Двійкове додавання а) – приклад на двійкове додавання; б) - скорочена форма таблиці двійкового додавання
Рис. 7.5.2. Двійкове додавання а) – приклад на двійкове додавання; б) - скорочена форма таблиці двійкового додавання Рішення виглядає простим, доки ми не доходимо до розряду двійок, де треба знайти двійкову суму. В десятковій системі ця сума дорівнює 3, що відповідає числу 11. Цей випадок не відображений на рис. 7.5.1. Сума 1+1+1 може виникнути в будь-якому розряді, за винятком розряду одиниць. В нову (скорочену) таблицю на рис. 7.5.2,б включена ще одна можлива комбінація 1+1+1.
Ця таблиця справедлива для всіх розрядів двійкових чисел, за виключенням розряду одиниць.
У відповідній таблиці дійсності (табл. 7.5.1) надано всі можливі комбінації двійкових однорозрядних доданків А, В і сигналу переносу Сin.
Табл.7.5.1. Таблиця дійсності повного суматора
| Входи | Виходи | |||
| Сin | В | А | S | С0 |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
| Перенос + В + А | Сума | Перенос | ||
Повні суматори використовуються для складання всіх двійкових розрядів за виключенням одиниць. Вони повинні мати додатковий вхід переносу.
Повний суматор – 3-входова схема. Сигнали на його виходах S і С0 отримуються внаслідок складання трьох вхідних сигналів (на входах А, В і Сin).
На рис. 7.5.3 показана розгорнута логічна схема повного суматора. Вона основана на структурній схемі з двома напівсуматорами.
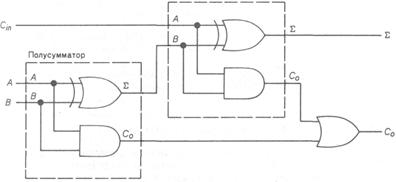

Напівсуматори і суматори зазвичай використовують разом. Велика кількість схем, аналогічних до напівсуматорів і повних суматорів, є в складі мікропроцесорних арифметично-логічних приладів (АЛП). Мікропроцесорні АЛП можуть виконувати і операції віднімання, при цьому використовуються ті ж самі напівсуматори і суматори.
Певним чином поєднуючи між собою напівсуматори та повні суматори отримують пристрої, що одночасно виконують додавання декількох двійкових розрядів. Пристрій, схема якого показана на рис. 7.5.5. виконує операцію додавання двох 3-розрядних чисел. Числа-доданки А2А1А0 і В2В1В0. Сигнали, що відповідають значенням розряду одиниць в доданках, поступають на вхід суматора розряду одиниць (напівсуматора). Вхідними сигналами для повного суматора розряду двійок є сигнал переноса з виходу напівсуматора (подається на вхід Сin) і значення А1 і В1 розряду двійок і доданків. Далі суматор четвірок складає А2 і В2 і сигнал переносу з суматора двійок. На двійковому виході пристрою (показано в правому нижньому куті рис. 7.5.5) встановлюється двійкова сума.
В результаті додавання двох 3-розрядних двійкових чисел можливо отримати 4-розрядне число, тому на індикаторі суми маємо додатковий розряд вісімок. Зверніть увагу, що даний розряд пов’язаний з виходом (С0) суматора четвірок.
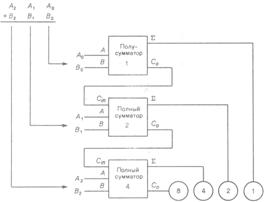
Рис. 7.5.5. 3-розрядний паралельний суматор
Логіка роботи розглядуваного 3-розрядного суматора майже не відрізняється від послідовності операцій , що виконуються при додаванні вручну (додаванні однорозрядних чисел плюс перенос в наступний розряд). Однак електронний суматор виконує дані операції набагато швидше.
Ще раз зазначимо, що в багаторозрядних суматорах напівсуматори використовуються лише для додавання в розряді одиниць; у всіх iнших розрядах використовуються повні суматори. Описаний вище 3-розрядний суматор називається паралельним суматором.
В паралельному суматорі інформаційні біти всіх розрядів поступають на входи одночасно. Результат (сума) з’являється на виході практично миттєво. Паралельний суматор на рис. 7.5.5 відноситься до класу комбінаційних логічних схем. Для фіксації даних на входах і виходах суматорів зазвичай використовують різноманітні додаткові регістри.
Похожие работы
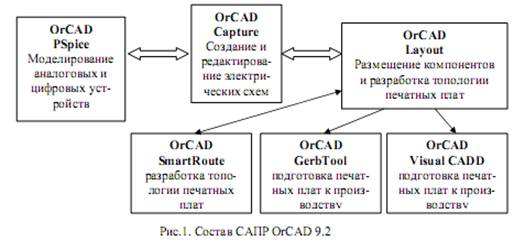
... цих проектів, їх компіляції, комп’ютерного моделювання, загрузки проекту на кристал ПЛІС. Програмні продукти фірм Xilinx та Altera на сьогоднішній день є найбільш поширеними САПР для проектування цифрових пристроїв на ПЛІС. Серед програмних продуктів Xіlіnx є як відносно прості вільно розповсюджувані системи, так і потужні інтегровані пакети, що дозволяють розробляти ПЛІС еквівалентної ємності бі ...
... КП, відповідно; X Offset, Y Offset – зсув точки підключення траси відносно геометричного центру КП по осях X і Y, відповідно. Таблиця апертур (Apertures) містить опис використовуваних апертур. Таблиця Layers містить список шарів, використовуваних OrCAD Layout. Шари можуть бути наступних типів: Routing – шар трасування; Plane – шар металізації; Drill – шар символів отворів; Jumper – шар ...
... результаты отчета. Они являются кульминационным пунктом отчета и должны быть разумными, хорошо определенными, перечисленными и обоснованными [11].Практика дистанционного образования с использованием Internet Шутилов Ф.В. Особенности заочного образования - в необходимости обеспечить высокий уровень знаний при значительно меньшем времени непосредственного личного общения студентов с преподавателем. ...




0 комментариев