Метод трапеций

5.3 Метод трапеций

Выведем формулу трапеций так же, как и формулу прямоугольников, из геометрических соображений. Заменим график функции y = f(x) (рис.5.1) ломаной линией (рис.5.7), полученной следующим образом. Из точек a = x₀, x₁, x₂,…, x_n = b проведем ординаты до пересечения с кривой y = f(x). Концы ординат соединим прямолинейными отрезками.

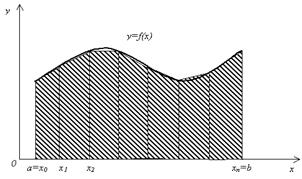
Рис. 5.7

Тогда площадь криволинейной трапеции приближенно можно считать равной площади фигуры, составленной из трапеций. Так как площадь трапеции, построенной на отрезке [x_i, x_i+1] длины h =  , равна h , то, пользуясь этой формулой для i = 0, 2, … , n – 1, получим квадратурную формулу трапеций:

I=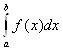»I_тр=h= (5.7)

Оценка погрешности. Для оценки погрешности формулы трапеций воспользуемся следующей теоремой.

Теорема 5.2. Пусть функция f дважды непрерывно дифференцируема на отрезке [a, b]. Тогда для формулы трапеций справедлива следующая оценка погрешности:

| I – I_тр| £  h², (5.8)

где M₂  = |f "(x)|.

Пример 5.2.

Вычислим значение интеграла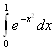 по формуле трапеций (5.7) и сравним полученный результат с результатом примера 5.1.

Используя таблицу значений функции eиз примера 5.1 и производя вычисления по формуле трапеций (5.7), получим: I_тр = 0.74621079.

Оценим погрешность полученного значения. В примере (5.1) получили оценку: | f "(x)| £ M₂ = 2. Поэтому по формуле (5.8)

 I – I_тр | £ (0.1)²  » 1.7× 10^-3.

Сравнивая результаты примеров 5.1 и 5.2, видим, что метод средних прямоугольников имеет меньшую погрешность, т.е. он более точный.

5.4 Метод Симпсона (метод парабол)

Заменим график функции y = f(x) на отрезке [x_i, x_i+1], i = 0, 2, … , n – 1, параболой, проведенной через точки (x_i, f(x_i)), (x,f(x)), (x_i+1, f(x_i+1)), где x - середина отрезка [x_i, x_i+1]. Эта парабола есть интерполяционный многочлен второй степени L₂(x) с узлами x_i, x, x_i+1. Нетрудно убедиться, что уравнение этой параболы имеет вид:

y = L₂(x) =

f(x) + (x – x) + (x - x)², (5.9)

где h = .

Проинтегрировав функцию (5.9) на отрезке [x_i, x_i+1], получим

I_i = 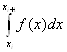»  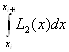= ( f(x_i) + 4f(x) + f(x_i+1)). (5.10)

Суммируя выражение (5.10) по i = 0, 1, 2, … , n – 1, получим квадратурную формулу Симпсона (или формулу парабол):

 I =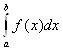» I_С= ( f(x₀) + f(x_n) + 4 + 2). (5.11)

Оценка погрешности. Для оценки погрешности формулы Симпсона воспользуемся следующей теоремой.

Теорема 5.2. Пусть функция f имеет на отрезке [a, b] непрерывную производную четвертого порядка f ⁽⁴⁾(x). Тогда для формулы Симпсона (5.9) справедлива следующая оценка погрешности:

| I – I_С| £ h⁴, (5.12)

где M₄ = | f ⁽⁴⁾(x)|.

Замечание. Если число элементарных отрезков, на которые делится отрезок [a, b], четно , т.е. n = 2m, то параболы можно проводить через узлы с целыми индексами, и вместо элементарного отрезка [x_i, x_i+1] длины h рассматривать отрезок [x_2i, x_2i+2] длины 2h. Тогда формула Симпсона примет вид:

I » (f(x₀) + f(x_2m) + 4 + 2), (5.13)

а вместо оценки (5.10) будет справедлива следующая оценка погрешности:

| I – I_С| £  h⁴, (5.14)

Пример 5.3.

Вычислим значение интеграла 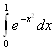 по формуле Симпсона (5.11) и сравним полученный результат с результатами примеров 5.1 и 5.2.

Используя таблицу значений функции eиз примера 5.1 и производя вычисления по формуле Симпсона (5.11) , получим:

I_С = 0.74682418.

Оценим погрешность полученного значения. Вычислим четвертую производную f ⁽⁴⁾(x).

f ⁽⁴⁾(x) = (16x⁴ – 48x² + 12) e, | f ⁽⁴⁾(x)| £ 12.

Поэтому

| I – I_С | £ (0.1)⁴ » 0.42 × 10^-6.

Сравнивая результаты примеров 5.1, 5.2 и 5.3, видим , что метод Симпсона имеет меньшую погрешность, чем метод средних прямоугольников и метод трапеций.

Похожие работы

Лекции по вычислительной математике

Скачать

10356

0

0

... . Рассмотрение метода ветвей и границ для решения задачи о коммивояжере удобнее всего проводить на фоне конкретного примера. Пользуясь введенными здесь обозначениями, мы проводим это описание в следующей лекции. Введем некоторые термины. Пусть имеется некоторая чис- ловая матрица. Привести строку этой матрицы означает выде-лить в строке минимальный элемент (его называют константой приведения) ...

Основные задачи вычислительной математики

Скачать

7721

1

1

... если  - предельная абсолютная погрешность приближённого числа , то  (1.2) отсюда следует, что  (1.3) Значение предельной абсолютной погрешности, обычно, подбирается интуитивно по смыслу задачи. Пример 2: Определить предельную абсолютную погрешность числа , заменяющего число , точное значение которого нам неизвестно. Так как мы знаем, что , ...

Выдающиеся личности в истории вычислительной техники. Августа Ада Лавлейс

Скачать

37333

0

0

... удивили меня…, хоть речь идёт обо мне самой. Они действительно написаны прекрасным стилем, который превосходит стиль самого очерка" /2/. 2.3. Рождение первенца и критическое перенапряжение Августа Ада Лавлейс работает с большим напряжением. В письмах к Бэббиджу она неоднократно жалуется на утомление, болезни, плохое самочувствие. Наконец, 6 августа Бэббидж отсылает Аде свои последние замечания ...

Роль женщин в развитии вычислительной техники

Скачать

54819

0

0

... в Украине, бывшем Советском Союзе и за рубежом научная школа теоретического программирования. В 2001-м году ее не стало... Но не только в научном плане велика роль женщин в развитии вычислительной техники. Со временем образуется огромное количество различных фирм по разработке и продаже программного и аппаратного обеспечения. Следовательно, разыгрываются человеческие трагедии капиталистического ...