Навигация
Модифицированные методы Эйлера
6.3 Модифицированные методы Эйлера
Первый модифицированный метод Эйлера. Суть этого метода состоит в следующем. Сначала вычисляются вспомогательные значения искомой функции y![]() в точках t
в точках t![]() = ti +
= ti + ![]() с помощью формулы:
с помощью формулы:
y![]() = yi +
= yi + ![]() fi = yi +
fi = yi +![]() f(ti, yi).
f(ti, yi).
Затем находится значение правой части уравнения (6.1) в средней точке
f![]() = f(t
= f(t![]() , y
, y![]() )
)
и затем полагается
yi+1 = yi + h f![]() , i = 0, 1, …, n – 1. (6.12)
, i = 0, 1, …, n – 1. (6.12)
Формулы (6.12) являются расчетными формулами первого модифицированного метода Эйлера.
Первый модифицированный метод Эйлера является одношаговым методом со вторым порядком точности
Второй модифицированный метод Эйлера – Коши. Суть этого метода состоит в следующем. Сначала вычисляются вспомогательные значения
![]() = yi + h f(ti, yi). (6.13)
= yi + h f(ti, yi). (6.13)
Затем приближения искомого решения находятся по формуле:
yi+1 = yi + ![]() [f(ti, yi) + f(ti+1,
[f(ti, yi) + f(ti+1, ![]() )], i = 0, 1, …, n – 1. (6.14)
)], i = 0, 1, …, n – 1. (6.14)
Формулы (6.14) являются расчетными формулами второго модифицированного метода Эйлера – Коши.
Второй модифицированный метод Эйлера – Коши, так же, как и первый, является одношаговым методом со вторым порядком точности.
Оценка погрешности. Приближенная оценка погрешности модифицированных методов Эйлера осуществляется как и для простого метода Эйлера с использованием правила Рунге (см. предыдущий раздел 6.2). Так как оба модифицированных метода Эйлера имеют второй порядок точности, т. е. p = 2, то оценка погрешности (6.6) примет вид
R » ![]() |y
|y![]() - y
- y![]() |. (6.15)
|. (6.15)
Используя правило Рунге, можно построить процедуру приближенного вычисления решения задачи Коши модифицированными методами Эйлера с заданной точностью e. Нужно, начав вычисления с некоторого значения шага h, последовательно уменьшать это значение в два раза, каждый раз вычисляя приближенное значение y![]() , i = 0, 1, …, n. Вычисления прекращаются тогда, когда будет выполнено условие:
, i = 0, 1, …, n. Вычисления прекращаются тогда, когда будет выполнено условие:
R » ![]() |y
|y![]() - y
- y![]() | < e. (6.16)
| < e. (6.16)
Приближенным решением будут значения y![]() , i = 0, 1, …, n.
, i = 0, 1, …, n.
Пример 6.2.
Применим первый модифицированный метод Эйлера для решения задачи Коши
y' (t) = y – ![]() , y(0) = 1,
, y(0) = 1,
рассмотренной ранее в примере 6.1.
Возьмем шаг h = 0.2. Тогда n = ![]() = 5.
= 5.
В соответствии с (6.3) получим расчетную формулу первого модифицированного метода Эйлера:
yi+1 = yi + h f![]() = yi + 0.2 f
= yi + 0.2 f![]() , где
, где
f![]() = f(t
= f(t![]() , y
, y![]() ) = y
) = y![]() –
– ![]() ,
,
t![]() = ti +
= ti + ![]() = ti + 0.1,
= ti + 0.1,
y![]() = yi +
= yi +![]() f(ti, yi) = yi +0.1
f(ti, yi) = yi +0.1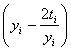 ,
,
t0 = 0, y0 = 1, i = 0, 1, …, 4.
Решение представим в виде таблицы 6.3:
Таблица 6.3
| i | ti | yi |
| t | y | h f |
| 0 1 2 3 4 5 | 0 0.2 0.4 0.6 0.8 1.0 | 1 1.1836 1.3426 1.4850 1.6152 1.7362 | 0.1 0.0850 0.0747 0.0677 0.0625 | 0.1 0.3 0.5 0.7 0.9 | 1.1 1.2682 1.4173 1.5527 1.6777 | 0.1836 0.1590 0.1424 0.1302 0.1210 |
Третий столбец таблицы 6.3 содержит приближенное решение yi, i = 0, 1, …, 5.
Сравним полученное приближенное решение с точным решением (6.11), представленном в таблице 6.2. Виднм, что погрешность составляет R = ![]() | y(ti) – yi| = 0.0042.
| y(ti) – yi| = 0.0042.
Пример 6.3.
Применим второй модифицированный метод Эйлера – Коши для решения задачи Коши
y' (t) = y – ![]() , y(0) = 1,
, y(0) = 1,
рассмотренной ранее в примерах 6.1 и 6.2. Так же, как и ранее, зададим шаг h = 0.2. Тогда n = ![]() = 5.
= 5.
В соответствии с (6.14) получим расчетную формулу метода Эйлера – Коши:
yi+1 = yi + ![]() [f(ti, yi) + f(ti+1,
[f(ti, yi) + f(ti+1, ![]() )] = yi + 0.1[f(ti, yi) + f(ti+1,
)] = yi + 0.1[f(ti, yi) + f(ti+1, ![]() )],
)],
где
f(ti, yi) = yi – ![]()
![]() = yi + h f(ti, yi) = yi + 0.1
= yi + h f(ti, yi) = yi + 0.1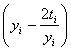
t0 = 0, y0 = 1, i = 0, 1, …, 4.
Решение представим в виде таблицы 6.4:
Таблица 6.4
| i | ti | yi |
| ti+1 |
| f(ti+1, |
| 0 1 2 3 4 5 | 0 0.2 0.4 0.6 0.8 1.0 | 1 1.1867 1.3484 1.4938 1.6272 1.7542 | 0.1 0.0850 0.0755 0.0690 0.0645 | 0.2 0.4 0.6 0.8 1.0 | 1.2 1.3566 1.4993 1.6180 1.7569 | 0.867 0.767 0.699 0.651 0.618 |
Таблица 6.4 заполняется последовательно по строкам, сначала первая строка, затем вторая и т. д. Третий столбец таблицы 6.4 содержит приближенное решение yi, i = 0, 1, …, 5.
Сравним полученное приближенное решение с точным решением (6.11), представленном в таблице 6.2. Видим, что погрешность составляет R = ![]() | y(ti) – yi| = 0.0222.
| y(ti) – yi| = 0.0222.
Похожие работы
... . Рассмотрение метода ветвей и границ для решения задачи о коммивояжере удобнее всего проводить на фоне конкретного примера. Пользуясь введенными здесь обозначениями, мы проводим это описание в следующей лекции. Введем некоторые термины. Пусть имеется некоторая чис- ловая матрица. Привести строку этой матрицы означает выде-лить в строке минимальный элемент (его называют константой приведения) ...
... если - предельная абсолютная погрешность приближённого числа , то (1.2) отсюда следует, что (1.3) Значение предельной абсолютной погрешности, обычно, подбирается интуитивно по смыслу задачи. Пример 2: Определить предельную абсолютную погрешность числа , заменяющего число , точное значение которого нам неизвестно. Так как мы знаем, что , ...
... удивили меня…, хоть речь идёт обо мне самой. Они действительно написаны прекрасным стилем, который превосходит стиль самого очерка" /2/. 2.3. Рождение первенца и критическое перенапряжение Августа Ада Лавлейс работает с большим напряжением. В письмах к Бэббиджу она неоднократно жалуется на утомление, болезни, плохое самочувствие. Наконец, 6 августа Бэббидж отсылает Аде свои последние замечания ...
... в Украине, бывшем Советском Союзе и за рубежом научная школа теоретического программирования. В 2001-м году ее не стало... Но не только в научном плане велика роль женщин в развитии вычислительной техники. Со временем образуется огромное количество различных фирм по разработке и продаже программного и аппаратного обеспечения. Следовательно, разыгрываются человеческие трагедии капиталистического ...

0 комментариев