Вычислительные методы
Метод деления отрезка пополам (метод дихотомии, метод бисекции)
Метод Ньютона (метод касательных)
Метод секущих (метод хорд)
Постановка задачи
Метод исключения Гаусса с выбором главного элемента по столбцу
Вычисление определителя методом исключения Гаусса
Метод Зейделя
Интерполяция функции многочленами Лагранжа
Аппроксимация функций. Метод наименьших квадратов
Квадратичная аппроксимация (m = 2)
Линейная аппроксимация (m =1)
Постановка задачи численного интегрирования
Метод трапеций
Правило Рунге практической оценки погрешности
Метод Эйлера
Модифицированные методы Эйлера
Метод Рунге – Кутта
Методом деления отрезка пополам найти корень уравнения
Решение системы линейных алгебраических уравнений простым методом исключения Гаусса
Навигация
Решение системы линейных алгебраических уравнений простым методом исключения Гаусса
Вычислительная математика
100779
знаков
18
таблиц
23
изображения
11. Решение системы линейных алгебраических уравнений простым методом исключения Гаусса.
Контрольный пример. Решить систему уравнений
2.1x1 – 4.5x2 – 2.0x3= 19.07
3.0x1 + 2.5x2 + 4.3x3 = 3.21
–6.0x1 + 3.5x2 + 2.5x3 = –18.25
12. Решение системы линейных алгебраических уравнений методом исключения Гаусса с выбором главного элемента по столбцу
Контрольный пример. Решить систему уравнений
1.00x1 + 0.42x2
+ 0.54x3 + 0.66x4
= 0.3
0.42x1 + 1.00x2 + 0.32x3 + 0.44x4 = 0.5
0.54x1 + 0.32x2 + 1.00x3 + 0.22x4 = 0.7
0.66x1 + 0.22x2 + 1.00x3 – 1.0x4 = 0.9
13. Решение системы линейных алгебраических уравнений методом простых итераций Якоби.
Контрольный пример. Решить систему уравнений с точностью e = 10-5.
–3.0x1 + 0.5x2
+ 0.5x3 = –56.65
0.5x1 – 6.0x2 + 0.5x3 = –160
0.5x1 + 0.5x2 – 3.0x3 = –210
14. Решение системы линейных алгебраических уравнений методом Зейделя.
Контрольный пример. Решить систему уравнений с точностью e = 10-5.
10x1 + 2x2 + x3 = 10
x1 + 10x2 + 2x3 = 12
x1 + x2 + 10x3 = 8
15. Вычисление определителя методом исключения Гаусса.
Контрольный пример. Вычислить определитель
det A = 3.0 1.5 0.1 1.0
0.4 0.5 4.0 6.5
0.3 1.2 3.0 0.7
1.8 2.2 2.5 1.4
16. Вычисление обратной матрицы методом исключения Гаусса.
Контрольный пример. Вычислить обратную матрицу A-1 для матрицы
A = 6.4375 2.1849 –3.7474 1.8822
2.1356 5.2101 1.5220 –1.1234
–3.7362 1.4998 7.6421 1.2324
1.8666 –1.1004 1.2460 8.3312
17. Интерполяция функции многочленами Лагранжа.
Контрольный пример. Построить интерполяционный многочлен Лагранжа для функции y = e
по точкам, заданным таблицей
| x | 0.00 | 0.25 | 0.50 | 0.75 | 1.00 |
| e | 1.0000000 | 0.9394131 | 0.7788008 | 0.7389685 | 0.3678794 |
Оценить погрешность интерполяции на отрезке [0, 1]. Вычислить y(0.4) и y(0.8).
18. Метод наименьших квадратов. Линейная и квадратичная аппроксимация
Численное интегрирование функций одной переменной
Указание. В курсовых работах 19 – 22 необходимо проанализировать предложенные методы численного интегрирования функций одной переменной, написать алгоритмы и программы этих методов. С помощью этих программ решить контрольный пример. Проконтролировать погрешность, использовав правило Рунге (п. 5.5). Если можно, вычислить точное значение интеграла. Дать сравнительный анализ полученных результатов.
19. Решение задачи численного интегрирования методом средних, левых и правых прямоугольников.
Контрольный пример. Вычислить 
, n = 10.
20. Решение задачи численного интегрирования методом средних прямоугольников и трапеций.
Контрольный пример. Вычислить 
, n = 10.
21. Решение задачи численного интегрирования методом средних прямоугольников и Симпсона.
Контрольный пример. Вычислить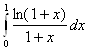 
, n = 10.
22. Решение задачи численного интегрирования методом трапеций и Симпсона.
Контрольный пример. Вычислить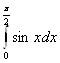 
, n = 10.
Численное решение дифференциальных уравнений
Указание. В курсовых работах 23 – 26 необходимо проанализировать предложенные методы численного решения задачи Коши, написать алгоритмы и программы этих методов. С помощью этих программ решить контрольный пример. Проконтролировать погрешность, использовав правило Рунге (пп. 6.2, 6.3, 6.4). Найти точное решение. Дать сравнительный анализ полученных результатов.
23. Решение задачи Коши для обыкновенных дифференциальных уравнений простым методом Эйлера и первым модифицированным методом Эйлера.
Контрольный пример. Найти численное решение задачи Коши
y' = y3, y(0) = 0.5на отрезке [0, 2] с шагом h = 0.2.
24. Решение задачи Коши для обыкновенных дифференциальных уравнений простым методом Эйлера и вторым модифицированный метод Эйлера – Коши.
Контрольный пример. Найти численное решение задачи Коши
y' = t2, y(0) = 1на отрезке [0, 2] с шагом h = 0.2.
25. Решение задачи Коши для обыкновенных дифференциальных уравнений первым модифицированным методом Эйлера и вторым модифицированный метод Эйлера – Коши.
Контрольный пример. Найти численное решение задачи Коши
y' = sint, y(0) = 1на отрезке [0, 2] с шагом h = 0.2.
26. Решение задачи Коши для обыкновенных дифференциальных уравнений простым методом Эйлера и методом Рунге – Кутта четвертого порядка точности.
Контрольный пример. Найти численное решение задачи Коши
y' = 2cost, y(0) = 0.на отрезке [0, 2] с шагом h = 0.2.
Краткие сведения о математиках
Гаусс Карл Фридрих (1777 – 1855) – немецкий математик и физик, работы которого оказали большое влияние на развитие высшей алгебры, геометрии, теории чисел, теории электричества и магнетизма.
Зейдель Людвиг (1821 – 1896) – немецкий астроном и математик.
Коши Огюстен Луи (1789 – 1857) – французский математик, один из создателей современного математического анализа, теории дифференциальных уравнений и др.
Крамер Габриэль (1704 – 1752) – швейцарский математик.
Кутта В. М. (1867 – 1944) – немецкий математик.
Лагранж Жозеф Луи (1736 – 1813) – французский математик, механик и астроном. Один из создателей математического анализа, вариационного исчисления, классической аналитической механики.
Липшиц Рудольф (1832 – 1903) – немецкий математик.
Лейбниц Готфрид Вильгельм (1646 – 1716) – немецкий математик, физик и философ. Один из создателей дифференциального и интегрального исчислений.
Ньютон Исаак (1643 – 1727) – английский физик, механик, астроном, заложивший основы современного естествознания.
Рунге Карл Давид Тольме (1856 – 1927) – немецкий физик и математик.
Симпсон Томас (1710 – 1761) – английский математик.
Тейлор Брук (1685 – 1731) – английский математик и философ. Широко известная формула разложения функции в степенной ряд была получена им в 1712 г.
Эйлер Леонард (1707 – 1783) – математик, физик, механик, астроном. Родился в Швейцарии, с 1726 по 1741 г. и с 1776 по 1783 г. работал в России.
Якоби Карл Густав Якоб (1804 – 1851) – немецкий математик.
Список литературы
1. Амосов А., Дубинский Ю. А., Копченова Н.В. Вычислительные методы для инженеров: Учеб. пособие. – М.: Высш. шк., 1994.
2. Бахвалов Н. С. Численные методы. – М.: Наука, 1973.
3. Волков Е. А. Численные методы. – М.: Наука, 1987.
4. Дьяконов В. П. Математическая система Maple V R3/R4/R5. – М.: Изд-во "СОЛОН", 1998.
5. Калиткин Н.Н. Численные методы. – М.: Наука, 1978.
6. Копченова Н.В., Марон И. А. Вычислительная математика в примерах и задачах. – М.: Наука, 1972.
7. Пирумов У.Г. Численные методы.: Учебное пособие. – М.: Изд-во МАИ, 1998.
Похожие работы
... . Рассмотрение метода ветвей и границ для решения задачи о коммивояжере удобнее всего проводить на фоне конкретного примера. Пользуясь введенными здесь обозначениями, мы проводим это описание в следующей лекции. Введем некоторые термины. Пусть имеется некоторая чис- ловая матрица. Привести строку этой матрицы означает выде-лить в строке минимальный элемент (его называют константой приведения) ...
... если - предельная абсолютная погрешность приближённого числа , то (1.2) отсюда следует, что (1.3) Значение предельной абсолютной погрешности, обычно, подбирается интуитивно по смыслу задачи. Пример 2: Определить предельную абсолютную погрешность числа , заменяющего число , точное значение которого нам неизвестно. Так как мы знаем, что , ...
... удивили меня…, хоть речь идёт обо мне самой. Они действительно написаны прекрасным стилем, который превосходит стиль самого очерка" /2/. 2.3. Рождение первенца и критическое перенапряжение Августа Ада Лавлейс работает с большим напряжением. В письмах к Бэббиджу она неоднократно жалуется на утомление, болезни, плохое самочувствие. Наконец, 6 августа Бэббидж отсылает Аде свои последние замечания ...
... в Украине, бывшем Советском Союзе и за рубежом научная школа теоретического программирования. В 2001-м году ее не стало... Но не только в научном плане велика роль женщин в развитии вычислительной техники. Со временем образуется огромное количество различных фирм по разработке и продаже программного и аппаратного обеспечения. Следовательно, разыгрываются человеческие трагедии капиталистического ...
0 комментариев