Навигация
Интерполяция функции многочленами Лагранжа
4.3 Интерполяция функции многочленами Лагранжа
Рассмотрим другой подход к приближению функции многочленами. Пусть функция y = f(x) определена на отрезке [a, b] и известны значения этой функции в некоторой системе узлов xi Î [a, b], i = 0, 1, … , n. Например, эти значения получены в эксперименте при наблюдении некоторой величины в определенных точках или в определенные моменты времени x0, x1, … , xn. Обозначим эти значения следующим образом: yi = f(xi), i = 0, 1, … , n. Требуется найти такой многочлен P(x) степени m,
P(x) = a0 + a1x + a2x2 + … + amxm, (4.5)
который бы в узлах xi, i = 0, 1, … , n принимал те же значения, что и исходная функция y = f(x), т. е.
P(xi) = yi, i = 0, 1, … , n. (4.6)
Многочлен (4.5), удовлетворяющий условию (4.6), называется интерполяционным многочленом.
Другими словами, ставится задача построения функции y = P(x), график которой проходит через заданные точки (xi, yi), i = 0, 1, … , n (рис. 4.1).
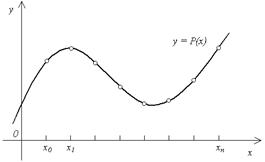
Рис. 4.1
Объединяя (4.5) и (4.6), получим:
a0 + a1xi + a2x![]() + … + amx
+ … + amx![]() = yi,i = 0, 1, … , n. (4.7)
= yi,i = 0, 1, … , n. (4.7)
В искомом многочлене P(x) неизвестными являются m +1 коэффициент a0 , a1, a2, …, am. Поэтому систему (4.7) можно рассматривать как систему из n +1 уравнений с m +1 неизвестными. Известно, что для существования единственного решения такой системы необходимо , чтобы выполнялось условие: m = n. Таким образом, систему (4.7) можно переписать в развернутом виде:
![]() a0 + a1 x0 + a2x
a0 + a1 x0 + a2x![]() + … + anx
+ … + anx![]() = y0
= y0
a0 + a1 x1 + a2x![]() + … + anx
+ … + anx![]() = y1
= y1
a0 + a1 x2 + a2x![]() + … + anx
+ … + anx![]() = y2 (4.8)
= y2 (4.8)
.
a0 + a1 xn + a2x![]() + … + anx
+ … + anx![]() = yn
= yn
Вопрос о существовании и единственности интерполяционного многочлена решает следующая теорема:
Теорема 4.1. Существует единственный интерполяционный многочлен степени n, удовлетворяющий условиям (4.6).
Имеются различные формы записи интерполяционного многочлена. Широко распространенной формой записи является многочлен Лагранжа
Ln(x) = ![]() =
= ![]() . (4.9)
. (4.9)
В частности, для линейной и квадратичной интерполяции по Лагранжу получим следующие интерполяционные многочлены:
L1(x) = y0![]()
![]() + y1
+ y1![]() ,
,
L2(x) = y0![]() +y1
+y1![]() + y2
+ y2![]() .
.
Пример 4.3.
Построим интерполяционный многочлен Лагранжа по следующим данным:
| x | 0 | 2 | 3 | 5 |
| y | 1 | 3 | 2 | 5 |
Степень многочлена Лагранжа для n +1 узла равна n. Для нашего примера многочлен Лагранжа имеет третью степень. В соответствии с (4.9)
L3(x) = 1![]() +3
+3![]() + 2
+ 2![]() + 5
+ 5![]() = 1 +
= 1 + ![]() x –
x – ![]() x2 +
x2 + ![]() x3.
x3.
Пример 4.4.
Рассмотрим пример использования интерполяционного многочлена Лагранжа для вычисления значения заданной функции в промежуточной точке. Эта задача возникает, например, когда заданы табличные значения функции с крупным шагом, а требуется составить таблицу значений с маленьким шагом.
Для функции y = sinx известны следующие данные.
| x | 0 | p/6 | p/3 | p/2 |
| y | 0 | ½ |
| 1 |
Вычислим y(0.25).
Найдем многочлен Лагранжа третьей степени:
L3(x) = 0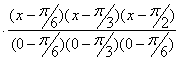 +
+ ![]()
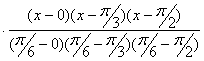 +
+
![]()
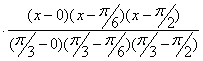 + 1
+ 1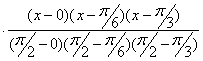 .
.
При x = 0.25 получим y(0.25) = sin 0.25 » 0.249.
Погрешность интерполяции. Пусть интерполяционный многочлен Лагранжа построен для известной функции f(x). Необходимо выяснить, насколько этот многочлен близок к функции в точках отрезка [a, b], отличных от узлов. Погрешность интерполяции равна |f(x) – Pn(x)|. Оценку погрешности можно получить на основании следующей теоремы.
Теорема 4.2. Пусть функция f(x) дифференцируема n +1 раз на отрезке [a, b], содержащем узлы интерполяции xi Î [a, b], i = 0, 1, … , n. Тогда для погрешности интерполяции в точке x Î [a, b] справедлива оценка:
|f(x) – Ln(x)|£ ![]() |wn+1(x)|, (4.10)
|wn+1(x)|, (4.10)
где
Mn+1 = ![]() |f(n+1)(x)|,
|f(n+1)(x)|,
wn+1(x) = (x – x0)(x – x1)…. (x – xn).
Для максимальной погрешности интерполяции на всем отрезке [a, b] справедлива оценка:
![]() |f(x) – Ln(x)| £
|f(x) – Ln(x)| £ ![]()
![]() |wn(x)| (4.11)
|wn(x)| (4.11)
Пример 4.5.
Оценим погрешность приближения функции f(x) = ![]() в точке x = 116
и на всем отрезке [a, b], где a = 100, b = 144, с помощью интерполяционного много члена Лагранжа L2(x) второй степени, построенного с узлами x0 = 100, x2 = 144.
в точке x = 116
и на всем отрезке [a, b], где a = 100, b = 144, с помощью интерполяционного много члена Лагранжа L2(x) второй степени, построенного с узлами x0 = 100, x2 = 144.
Найдем первую, вторую и третью производные функции f(x):
f '(x)= ![]() x– 1/2, f "(x)= –
x– 1/2, f "(x)= –![]() x–3/2, f'''(x)=
x–3/2, f'''(x)= ![]() x–5/2.
x–5/2.
M3 = ![]() | f'''(x)| =
| f'''(x)| = ![]() 100–5/2 =
100–5/2 = ![]() 10–5.
10–5.
В соответствии с (4.9) получим оценку погрешности в точке x = 116:
|![]() – L2(116)| £
– L2(116)| £ ![]() |(116 – 100)(116 – 121)(116 – 144)| =
|(116 – 100)(116 – 121)(116 – 144)| = ![]() 10–5×16×5×28 = 1.4×10 – 3.
10–5×16×5×28 = 1.4×10 – 3.
Оценим погрешность приближения функции f(x) = ![]() на всем отрезке в соответствии с (4.11):
на всем отрезке в соответствии с (4.11):
![]() |
|![]() – L2(x)| £
– L2(x)| £ ![]()
![]() |(x – 100)(x – 121)(x –144)| » 2.5×10–3.
|(x – 100)(x – 121)(x –144)| » 2.5×10–3.
Похожие работы
... . Рассмотрение метода ветвей и границ для решения задачи о коммивояжере удобнее всего проводить на фоне конкретного примера. Пользуясь введенными здесь обозначениями, мы проводим это описание в следующей лекции. Введем некоторые термины. Пусть имеется некоторая чис- ловая матрица. Привести строку этой матрицы означает выде-лить в строке минимальный элемент (его называют константой приведения) ...
... если - предельная абсолютная погрешность приближённого числа , то (1.2) отсюда следует, что (1.3) Значение предельной абсолютной погрешности, обычно, подбирается интуитивно по смыслу задачи. Пример 2: Определить предельную абсолютную погрешность числа , заменяющего число , точное значение которого нам неизвестно. Так как мы знаем, что , ...
... удивили меня…, хоть речь идёт обо мне самой. Они действительно написаны прекрасным стилем, который превосходит стиль самого очерка" /2/. 2.3. Рождение первенца и критическое перенапряжение Августа Ада Лавлейс работает с большим напряжением. В письмах к Бэббиджу она неоднократно жалуется на утомление, болезни, плохое самочувствие. Наконец, 6 августа Бэббидж отсылает Аде свои последние замечания ...
... в Украине, бывшем Советском Союзе и за рубежом научная школа теоретического программирования. В 2001-м году ее не стало... Но не только в научном плане велика роль женщин в развитии вычислительной техники. Со временем образуется огромное количество различных фирм по разработке и продаже программного и аппаратного обеспечения. Следовательно, разыгрываются человеческие трагедии капиталистического ...

0 комментариев