Навигация
Метод Эйлера
6.2 Метод Эйлера
Простейшим методом решения задачи Коши является метод Эйлера.
Будем решать задачу Коши
y' (t) = f(t, y(t)).
y(t0 ) = y0,
на отрезке [t0, T]. Выберем шаг h = ![]() , и построим сетку с системой узлов
, и построим сетку с системой узлов
ti = t0 + ih, i = 0, 1, …, n.
В методе Эйлера вычисляются приближенные значения функции y(t) в узлах сетки :yi » y(ti).
Заменив производную y' (t) конечными разностями на отрезках [ti, ti+1], i = 0, 1, …, n – 1, получим приближенное равенство:
![]() = f(ti, yi), i = 0, 1, …, n – 1,
= f(ti, yi), i = 0, 1, …, n – 1,
которое можно переписать так:
yi+1 = yi + h f(ti, yi), i = 0, 1, …, n – 1. (6.3)
Формулы (6.3) и начальное условие (6.2) являются расчетными формулами метода Эйлера.
Геометрическая интерпретация одного шага метода Эйлера заключается в том, что решение на отрезке [ti, ti+1] заменяется касательной y = y' (ti)( t - ti), проведенной в точке (ti, y(ti)) к интегральной кривой, проходящей через эту точку. После выполнения n шагов неизвестная интегральная кривая заменяется ломаной линией (ломаной Эйлера).
Оценка погрешности. Для оценки погрешности метода Эйлера воспользуемся следующей теоремой.
Теорема 6.2. Пусть функция f удовлетворяет условиям:
![]() £ K,
£ K, ![]() =
= ![]() £ L.
(6.4)
£ L.
(6.4)
Тогда для метода Эйлера справедлива следующая оценка погрешности:
R = ![]()
![]() | y(ti) – yi| £
| y(ti) – yi| £ ![]() =
= ![]() ,
,
где l – длина отрезка [t0, T]. Мы видим , что метод Эйлера имеет первый порядок точности.
Оценка погрешности метода Эйлера часто бывает затруднительна, так как требует вычисления производных функции f(t, y(t)). Грубую оценку погрешности дает правило Рунге (правило двойного пересчета), которое используется для различных одношаговых методов, имеющих p-ый порядок точности. Правило Рунге заключается в следующем. Пусть y![]() – приближения, полученные с шагом
– приближения, полученные с шагом ![]() , а y
, а y![]() – приближения, полученные с шагом h. Тогда справедливо приближенное равенство:
– приближения, полученные с шагом h. Тогда справедливо приближенное равенство:
|y![]() - y(ti)| »
- y(ti)| » ![]() |y
|y![]() - y
- y![]() | . (6.5)
| . (6.5)
Таким образом, чтобы оценить погрешность одношагового метода с шагом ![]() , нужно найти то же решение с шагом h и вычислить величину, стоящую справа в формуле (6.5), т е.
, нужно найти то же решение с шагом h и вычислить величину, стоящую справа в формуле (6.5), т е.
R » ![]() |y
|y![]() - y
- y![]() |
(6.6)
|
(6.6)
Так как метод Эйлера имеет первый порядок точности, т. е. p = 1, то приближенное равенство (6.6) примет вид
R » |y![]() - y
- y![]() | (6.7)
| (6.7)
Используя правило Рунге, можно построить процедуру приближенного вычисления решения задачи Коши с заданной точностью e. Нужно, начав вычисления с некоторого значения шага h, последовательно уменьшать это значение в два раза, каждый раз вычисляя приближенное значение y![]() , i = 0, 1, …, n. Вычисления прекращаются тогда, когда будет выполнено условие:
, i = 0, 1, …, n. Вычисления прекращаются тогда, когда будет выполнено условие:
R » ![]() |y
|y![]() - y
- y![]() | < e. (6.8)
| < e. (6.8)
Для метода Эйлера условие (6.8) примет вид
R» |y![]() - y
- y![]() | < e (6.9)
| < e (6.9)
Приближенным решением будут значения y![]() , i = 0, 1, …, n.
, i = 0, 1, …, n.
Пример 6.1.
Найдем решение на отрезке [0, 1] следующей задачи Коши:
y' (t) = y – ![]() ,
(6.10)
,
(6.10)
y(0) = 1.
Возьмем шаг h = 0.2. Тогда n = ![]() = 5.
= 5.
В соответствии с (6.3) получим расчетную формулу метода Эйлера:
yi+1 = yi + 0.2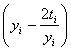 , y0 = 1, i = 0, 1, 2, 3, 4, 5.
, y0 = 1, i = 0, 1, 2, 3, 4, 5.
Решение представим в виде таблицы 6.1:
Таблица 6.1
| i | 0 | 1 | 2 | 3 | 4 | 5 |
| ti | 0 | 0.2 | 0.4 | 0.6 | 0.8 | 1.0 |
| yi | 1.0000 | 1.2000 | 1.3733 | 1.5294 | 1. 6786 | 1.8237 |
Уравнение (6.10) есть уравнение Бернулли. Его решение можно найти в явном виде:
y = ![]() .
(6.11)
.
(6.11)
Для сравнения точного и приближенного решений представим точное решение (6.11) в виде таблицы 6.2:
Таблица 6.2
| i | 0 | 1 | 2 | 3 | 4 | 5 |
| ti | 0 | 0.2 | 0.4 | 0.6 | 0.8 | 1.0 |
| y(ti) | 1.0000 | 1.1832 | 1.3416 | 1.4832 | 1. 6124 | 1.7320 |
Из таблицы видно, что погрешность составляет R = ![]() | y(ti) – yi| = 0.0917.
| y(ti) – yi| = 0.0917.
Похожие работы
... . Рассмотрение метода ветвей и границ для решения задачи о коммивояжере удобнее всего проводить на фоне конкретного примера. Пользуясь введенными здесь обозначениями, мы проводим это описание в следующей лекции. Введем некоторые термины. Пусть имеется некоторая чис- ловая матрица. Привести строку этой матрицы означает выде-лить в строке минимальный элемент (его называют константой приведения) ...
... если - предельная абсолютная погрешность приближённого числа , то (1.2) отсюда следует, что (1.3) Значение предельной абсолютной погрешности, обычно, подбирается интуитивно по смыслу задачи. Пример 2: Определить предельную абсолютную погрешность числа , заменяющего число , точное значение которого нам неизвестно. Так как мы знаем, что , ...
... удивили меня…, хоть речь идёт обо мне самой. Они действительно написаны прекрасным стилем, который превосходит стиль самого очерка" /2/. 2.3. Рождение первенца и критическое перенапряжение Августа Ада Лавлейс работает с большим напряжением. В письмах к Бэббиджу она неоднократно жалуется на утомление, болезни, плохое самочувствие. Наконец, 6 августа Бэббидж отсылает Аде свои последние замечания ...
... в Украине, бывшем Советском Союзе и за рубежом научная школа теоретического программирования. В 2001-м году ее не стало... Но не только в научном плане велика роль женщин в развитии вычислительной техники. Со временем образуется огромное количество различных фирм по разработке и продаже программного и аппаратного обеспечения. Следовательно, разыгрываются человеческие трагедии капиталистического ...

0 комментариев