Навигация
Виконання дії підведення під поняття
2.2. Виконання дії підведення під поняття.
Уміння застосовувати поняття є показником його засвоєння. На думку Н.О.Менчинської, якщо учень справді засвоїв поняття, то він уміє його і застосовувати.
Одним із провідних принципів педагогічної психології є принцип єдності знань і дій. Проте існують два роди знань: знання про предмети і явища навколишнього світу (а отже, і про поняття) і знання про дії, які з ними потрібно виконувати. Недоліком традиційного і сучасного навчання математики є недостатня увага до знань другого роду.
Часто учні, які добре знають означення математичних понять, не вміють застосовувати їх до доведення теорем і розв'язування задач, зокрема прикладних. Тому дії, адекватні знанням, зокрема поняттям, мають стати не тільки засобом, а й предметом засвоєння.
З погляду застосування понять важливу роль відіграють такі розумові дії, як «підведення до поняття» («дія розпізнавання») та обернена їй дія — відшукання наслідків. Остання означає, що від факту належності об'єкта до поняття приходять до системи властивостей, які має цей об'єкт. Потрібна спеціальна система вправ на підведення об'єктів до поняття. Для встановлення факту належності об'єкта до певного поняття потрібно перевірити наявність у об'єкта сукупності необхідних і достатніх властивостей. Якщо виявиться, що об'єкт не має хоча б однієї з істотних властивостей, роблять висновок, що до даного поняття він не належить. При цьому можна використовувати не тільки означення, а й теореми, що виражають властивості понять, які еквівалентні означенням у тому розумінні, що властивості понять, які стверджуються в них, можуть бути покладені в основу означень.
Наприклад, для встановленні належності чотирикутника до паралелограмів можна скористатися означенням паралелограма і теоремою про його ознаку. Разом вони є еквівалентними системами необхідних і достатніх властивостей.
Перелік операцій, що входять до складу дії підведення до поняття у випадку, коли істотні властивості пов'язані сполучником «і» чи сполучником «або», можна задати у вигляді такого навчального алгоритму. Щоб визначити, чи належить х до поняття у, потрібно:
1) виокремити властивості у;
2) з'ясувати, якими сполучниками пов'язані ці властивості;
3) якщо: а) сполучником «і», то перевірити, чи має х всі властивості у. Якщо так, то х належить до поняття у; якщо ні, то х не належить до поняття у; б) сполучником «або», то перевірити, чи має х хоча б одну властивість у. Якщо так, то х належить до поняття у; якщо ні, то х не належить до поняття у.
Якщо означення поняття має змішану структуру, тобто містить сполучник «і» та сполучник «або», то в алгоритмі потрібні додаткові вказівки.
Наведемо приклад. У курсі геометрії 7 класу учні ознайомлюються з означенням медіани трикутника. Доцільно ще на етапі введення означення чітко виділити дві істотні властивості, які воно містить і які лише разом утворююгь необхідну і достатню властивість належності об'єкта до поняття «медіана»: 1) медіана — це відрізок; 2) цей відрізок з'єднує вершину трикутника із серединою протилежної сторони.
Щоб встановити, чи є АВ медіаною трикутника АВС, потрібно: 1) пригадати означення медіани; 2) переконатися, що істотні властивості в ньому пов'язані сполучником «і»; 3) перевірити, чи має АО обидві властивості медіани.
2.3. Виконання дії виведення наслідків
Перелік операцій, що є складовими дії «відшукання наслідків», можна задати у вигляді такого навчального алгоритму: 1) назвати всі істотні властивості, які входять в означення поняття; 2) назвати інші істотні властивості, які вивчалися.
Наприклад, результати відшукання наслідків з поняття «рівнобедрений трикутник» можна сформулювати так. Якщо трикутник рівнобедрений, то: 1) дві сторони його рівні; 2) кути при основі рівні; 3) бісектриса кута при вершині є медіаною, проведеною до основи; 4) бісектриса кута при вершині є висотою, проведеною до основи; 5) пряма, що містить згадану бісектрису кута при вершині, є віссю симетрії цього трикутника.
З метою забезпечення передумов для формування умінь застосовувати поняття та їхні властивості до розв'язування задач і доведення теорем, доцільно після вивчення кожного з основних понять і відношень звести разом їхні істотні властивості, що містяться в означеннях і теоремах.
До таких понять слід віднести насамперед основні геометричні фігури та їхні властивості, відношення рівності, паралельності, перпендикулярності, основні види рівнянь, нерівностей, функцій. У міру вивчення курсу виникають нові можливості щодо доведення відношень рівності, паралельності й перпендикулярності відрізків, подібності фігур. Тому важливо сформулювати правила-орієнтири для доведення цих відношень.
Наприклад, щоб довести рівність двох відрізків, можна включити їх у трикутники і довести рівність цих трикутників або скористатися властивістю одного з рухів, або застосувати вектори, або довести, що ці відрізки є бічними сторонами рівнобедреного трикутника чи протилежними сторонами паралелограма (прямокутника, квадрата, ромба).
Основою застосування понять до розв'язування складніших задач і доведення теорем є прийом розумової діяльності, який дістав назву «аналіз через синтез», або переосмислення елементів задачі з погляду різних понять. У процесі застосування понять в учнів формується така важлива розумова дія, як конкретизація, оскільки використання знань у практичних ситуаціях пов'язане з переходом від абстрактного до конкретного. Дослідження педагогічної психології показують, що перехід від оперування абстрактними поняттями до конкретної практичної ситуації досить складний для школярів.
З цього приводу Л. С. Виготський писав, що шлях від абстрактного до конкретного виявляється тут не менш важким, ніж шлях сходження від конкретного до абстрактного. Багатьом учням складно одночасно виокремлювати абстрактні співвідношення в конкретних даних і абстрагуватися від наочного сприймання об'єктів. Для запобігання таким труднощам потрібно використовувати конкретні практичні ситуації ще в період формування абстрактних понять — розв'язувати задачі практичного змісту. Особливо корисними є практичні роботи на місцевості, екскурсії на сільськогосподарські та промислові підприємства.
Похожие работы
... сприймали готові образи, що їх дає вчитель, а й самі відтворювали геометричні форми в процесі моделювання, креслення, вирізування, малювання. Тому центральне місце у формуванні геометричних понять займає практика самих школярів. Сприймання простору передбачає сприймання відстані, на якій предмети розміщені від нас і один від одного, напряму, в якому вони перебувають, величини та форми предметів. ...
... може бути компетентною або некомпетентною в певних питаннях, тобто мати компетентність (компетентності) у певній галузі діяльності. Саме тому, одним із результатів навчання курсу «Застосування ІКТ у навчальному процесі з математики» вбачається формування в майбутніх вчителів відповідних ключових фахових компетентностей. Зазначене вище наштовхнуло на дослідження компетентностей: внаслідок чого ...
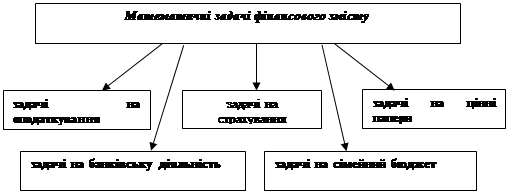
... у фінансовій сфері. Таке означення показує, що ці задачі можуть використовуватися протягом всього учбового процесу. Останнім часом посилився пошук шляхів активізації пізнавальної діяльності учнів у процесі навчання математики за допомогою задач. Введення математичних задач фінансового змісту в шкільний курс ґрунтується на засадах та принципах процесу активізації пізнавальної діяльності учнів. ...
... . В ході нашого дослідження ми також виконали поставлені нами завдання. Вивчення психолого-педагогічних, а також і методичних аспектів використання комп’ютерних ігор у процесі навчання молодших школярів на уроках математики дало змогу проаналізувати шляхи такого використання, на основі чого створити свої. Підбір навчальних ігор для уроків математики в початковій школі дав змогу зробити певні на



0 комментариев