Абстрактно-дедуктивний та конкретно-індуктивний методи навчання

2.4. Абстрактно-дедуктивний та конкретно-індуктивний методи навчання

Відомі конкретно-індуктивний і абстрактно-дедуктив­ний підходи до формування понять та їх означень. При першому з них учні спочатку спостерігають і аналізують кон­кретні об'єкти (числа, фігури, задачі та ін.), потім відокрем­люють і перераховують їх істотні ознаки і, нарешті, синтезують поняття та формулюють його означення. Так, при формуванні понять «прості» і «складені» числа можна запро­понувати учням розглянути такі множини чисел:

2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, ... 4, 6, 8, 9, 10, 12, 14, 15, 16, 18, 20, 21, 22, 24,

Учні визначають дільники чисел спочатку в першій мно­жині, а потім у другій; виявляють спільні і відмінні влас­тивості чисел обох рядів і означають поняття «просте число» і «складене число». При цьому слід звернути увагу на ті істотні ознаки, які узагальнюються і синтезуються в по­нятті.

Ці методи набули неабиякого поширення у навчанні математики. Вперше їх докладно проаналізував К.Ф.Лебединцев.

Суть абстрактно-дедуктивного методу навчання полягає в тому, що під час вивчення нового матеріалу вчитель відразу сам наводить означення понять, що вводяться, а потім наводить конкретні приклади об’єктів, що належать до цих понять. Формулюється й доводиться теорема, і лише після цього розглядаються конкретні приклади застосування нового теоретичного матеріалу.

Конкретно-індуктивний метод навчання протилежний абстрактно-дедуктивному. За цього методу пояснення нового матеріалу починається з розгляду прикладів. Використовуючи приклади, учні мають можливість виявити істотні властивості поняття, що вводиться. Це допомагає самостійно чи за допомогою вчителя сформулювати означення поняття. Рисунок до теореми дає змогу учням виявити властивості зображеної фігури і самостійно чи за допомогою вчителя сформулювати теорему.

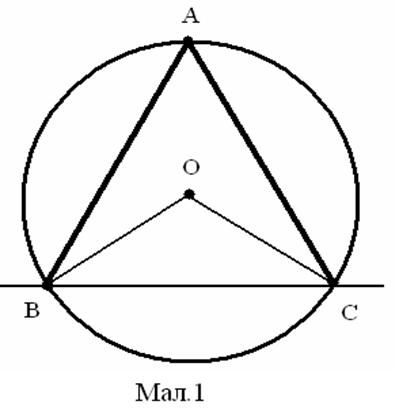
Наприклад, у 9 класі запроваджується поняття кута, вписаного в коло. За абстрактно-дедуктивного методу навчання вчитель відразу розпочинає з формулювання означення вписаного в коло кута й ілюструє його конкретними прикладами.

Означення. Кут, вершина якого лежить на колі, а сторони перетинають це коло, називається вписаним у коло (мал.1). Кут ВАС на малюнку вписано в коло. Його вершина А лежить на колі, а сторони перетинають коло в точках В і С.

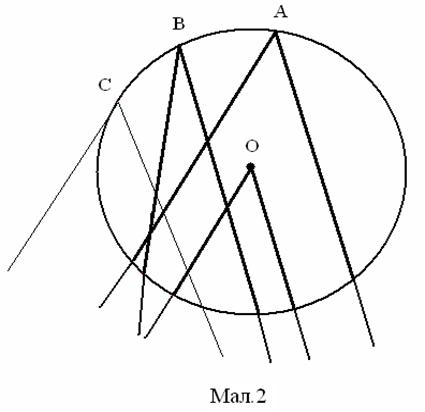
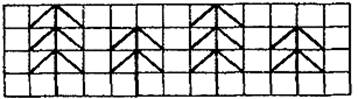
 За конкретно-індуктивного методу навчання вчитель пропонує учням рисунок на дошці (Мал.2), на якому зображено кілька різних кутів, пов’язаних з колом. Вписані кути на малюнку зображено одним кольором (тут – потовщеними лініями). Учням пропонується порівняти кути, виділені кольором, і назвати їхні істотні спільні властивості. Учні помічають, що вершини кутів лежать на колі, а сторони перетинають це коло. Вчитель пропонує учням сформулювати означення; звертає увагу на неістотні властивості вписаних кутів (величина, розміщення центра кола відносно сторін).

ВИСНОВКИ

Під час написання дипломної роботи було реалізовано та повністю виконано мету та завдання поставлені на початку дослідження даної проблеми.

В результаті аналізу психолого - педагогічної, методичної, математичної літератури з проблеми дослідження виявлено вікові особливості психологічного розвитку учнів основної школи, специфіку їх розумової, інтелектуальної діяльності, пам’яті, уваги, притаманну даному віковому періоду.

Визначаючи поняття як одну з основних форм мислення, підкреслюють його роль та значення у пізнанні. Саме мислення можна тоді розглядати як оперування поняттями, оскільки перехід від чуттєвих ступенів пізнання до абстрактного мислення характеризується як перехід від відображення його в поняттях і на їх основі, - в судженнях і інших логічних категоріях. Поняття виникають на основі суспільної практики і є продуктом багаторічного історичного розвитку пізнавальної діяльності людини.

Виявлені психолого-дидактичні закономірності формування математичних понять:

1.  Засвоєння математичних понять відбувається у процесі аналітико – синтетичної діяльності учнів, спрямованої на виявлення істотних загальних властивостей певного поняття;

2.  Усвідомлення неістотних властивостей поняття;

3.  Застосування нового поняття до розв’язування задач

В сучасних умовах дало змогу проаналізувати діяльність учнів в процесі викладання математики в основній школі та виявлені помилки, які допускаються при формуванні математичних понять.

До пізнавальної діяльності учнів щодо засвоєння математичних понять належать як загальні (аналіз синтез, порівняння, абстрагування, узагальнення тощо), так і специфічні розумові дії (підведення до поняття і обернена їй дія – виведення наслідків).

З розвитком науки математичні поняття формуються не лише на базі сприймань і уявлень (як початкові понят­тя), а на базі вже раніше встановлених понять.

До пізнавальної діяльності учнів щодо засвоєння математичних понять належать як загальні (аналіз синтез, порівняння, абстрагування, узагальнення тощо), так і специфічні розумові дії (підведення до поняття і обернена їй дія – виведення наслідків).

СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ

1.Державна національна програма «Освіта» («Україна XXI століття»): Затв. Постановою Кабінету Міністрів України від 03.11.93 № 896. — К.: Радуга, 1994. - 61 с.

2.Авдеева Н. Н. О статистическом образовании в школе // Математика в шк. — 1973. - № 3. - С. 4-8.

3.Лвраменко М. І. Таблиці з геометрії для 7 класу. — К.: Рад. шк., 1988.

4.Айзенштат Я. Й., Білоцерківська Б. Г. Розв'язування задач з математики в середній школі. — К.: Рад. шк., 1957. — 320 с

5.Агапов Г. И. Задачник по теории вероятностей. — М.: Высш. шк., 1986.

6.Алгебра: Учеб. для 7 кл. сред. шк. / Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нсш-ков, С. Б. Суворова; Под ред. С. А. Теляковского. — 3-е изд. — М.: Просвеще­ние, 1993. - 240 с.

10.Алгебра: Учеб. для 8 кл. сред. шк. / Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нсш-ков, С. Б. Суворова; Под ред. С. А. Теляковского. — 2-е изд. — М.: Просвеще­ние, 1991. - 238 с.

11.Алгебра і початки аналізу. Підруч. для 10 — 11 кл. серед, шк. / А. М. Колмого­ров, О. М. Абрамов, Ю. П. Дудніцин та ін.; За ред. А. М. Колмогорова. — К.: Освіта, 1992. - 350 с.

12.Алексюк А. М. Загальні методи навчання в школі. — 2-ге вид., персробл. і допов. — К.: Рад. шк., 1981. — 206 с.

13.Аллан Р., Вилльямс М. Математика на 5. Пособие для 1 —3 кл. начальной шк.: Пер. с англ. - М.: АСТ-Прссс, 1996. - 384 с.

14.Анастази А. Психологическое тестирование: Пер. с англ. / Под ред. К. М. Гу-ревича. - М., 1982. - Кн. 1. - 320 с.

15.Андерсон Дж. Думай, пытайся, развивайся: Пер. с англ. — СПб.: Азбука, 1996. — 92 с.

16.Апостолова Г. В. Планиметрия в опорных схемах. — К.: ФАКС, 2002. — 64 с.

17.Апостолова Г. В. Стереометрія в опорних схемах: Посіб. для 10 — 11 кл. — К.: Оракт, 1999. - 68 с.

18.Апостолова Г. В. Хитроумний модуль: Посіб. для 6 — 11 кл. — К.: Поліграф-сервіс, 2001. — 252 с.

19.Аташе Г. А. Дсятельностный подход в обучении. — Донецк: ЕЛИ-Пресс, 2001. - 160 с.

20.Ашкинузе В. Г., Шоластер Н. Н. Алгебра и элементарные функции. — М.: Просвещение, 1964. — 543 с.

21.Бабансъкий Ю. К. Методы обучения в современной общеобразовательной шко­ле. — М.: Просвещение, 1985. — 208 с.

22.Бабанский Ю. К. Оптимизация учебно-воспитательного процесса. — М.: Педагогика, 1982. — 192 с.

23.БалкМ. Б., БалкГ. Д. Математика после уроков. — М.: Просвещение, 1971. — 254 с.

24.Балк М. Б., Балк Г. Д. Поиск решения. — М.: Дет. лит., 1983.–143 с.

25.Балк М. Б., Балк Г. Д. Реальные применения мнимых чисел: Для ст. шк. возраста. — К.: Рад. шк., 1988. — 254 с.

26.Балл Г. А. Теория учебных задач: Психолого-педагогический аспект. — М.: Педагогика, 1990. — 184с.

27.Бараболин М. П. Методические основы развивающего обучения. — М.: Высш. шк., 1991. - 232 с.

28.Башмаков М. И. Мы учим и учимся математике в нашем общем доме-Европе // Математика в шк. — 2002. — № 1. — С. 3 — 6.

29.Башмаков М. И. Теория и практика продуктивного обучения. — М.: Нар. образование, 2000. — 248 с.

30.Башмаков М. И. Алгебра и начала анализа: Учеб. для 10 — 11 кл. сред. шк. — 2-е изд. — М.: Просвещение, 1992. — 350 с.

31.Бевз Г. П., Бевз В. Г., Владимирова Н. Г. Геометрия: Учеб. для 7 — 11 кл. сред. шк. — М.: Просвещение, 1992. — 352 с.

32.Бевз Г. П. Методика викладання математики: Навч. посіб. — К.: Вища шк., 1989. - 367 с.

33.Бевз Г. П. Методика розв'язування алгебраїчних задач. — К.: Рад. шк., 1975. — 240 с.

34.Бевз Г. П. Методика розв'язування стереометричних задач. — К.: Рад. шк., 1988.- 190 с.

35.Бевз Г. П. Математика, 6 кл. — К.: Вежа, 2002. — 224 с.

36.Бевз Г. П. Алгебра: Підруч. для 7-9 кл. - К.: Освіта, 2001. - 303 с.

38.Бевз Г. П. Геометрія: Підруч. для 10 — 11 кл. шк. з поглибл. вивченням мате­матики. — К.: Освіта, 2000. — 218 с.

39.Бевз Г. П., Бевз В. Г., Владимирова Н. Г. Геометрія: Проб, підруч. для 7 — 9 кл. — 2-ге вид. — К.: Вежа, 2004. — 312 с.

40.Бевз Г. П. Таблиці з математики для 8 класу. — К.: Рад. шк., 1978.

41.Бесполько В. П. Слагаемые педагогических технологий. — М.: Педагогика, 1989.- 119 с.

42.Бех I. Д. Особистісно зорієнтоване виховання: Наук.-метод, посіб. ін-т змісту і методів навчання. — К., 1998. — 204 с.

43.Груденов Я. И. Психолого-дидактическис основы методики обучения матема­тики. — М.: Педагогика, 1987. — 158 с.

44.Груденов Я. И. Совершенствование методики работы учителя математики: Кн. для учителя. — М.: Просвещение, 1990. — 223 с.

45.Гусев В. А., Иванов А. И., Шаболин О. Д. Изучение величин на уроках математики и физики в средней школе. — М.: Просвещение, 1991. — 79 с.

46.Давыдов В. В. Виды обобщения в обучении. — М.: Просвещение, 1972. — 423 с.

47.Давыдов В, В. Теория развивающего обучения / Междунар. ассоц. «Развива­ющее обучение». — М.: Интер, 1996. — 544 с.

48.Дементій О. І., Дементій С. В. Навчаючі задачі з геометрії: Посіб. для 7 — 9 кл. - К.: Торгсин, 1998. - 210 є.

49.Державний стандарт базової і повної середньої освіти // Математика в шк. — 2004. - № 2. - С 2-5.

50.Дидактика средней школы: Пособие для учителей / НИИ педагогики УССР; Под ред. В. А.Онищука. — К.: Рад. шк., 1987. — 350 с.

51.Дидактика средней школы. Некоторые проблемы современной дидактики: Учеб. пособие по спецкурсу / Под ред. М. Н. Скаткина. — М.: Просвещение, 1982. - 319 с.

52.Дорофеев Г. В. Строгость определений математических понятий с методичес­кой точки зрения // Математика в шк. — 1984. — № 3. — С. 56 — 60.

53.Дорофеев Г. В., Кузнецова Л. В., Суворова С. Б., Фирсов В. В. Дифференциа­ция в обучении математике // Математика в шк. — 1990. — № 4. — С. 15—21.

54.Дорофеев Г. В. О принципах отбора содержания математического образования // Математика в шк. - 1990. - № 6. - С. 3-5.

55.Дусавицкий А. К. Формула интереса. — М.: Педагогика, 1989. — 172 с.

56.Єріна А. М., Пальян 3. О. Теорія статистики: Практикум. — К.: Знання, 2002. - 235 с

57.Епишев О. Б., Крупич В. И. Учат школьников учиться математике: Форми­рование приемов учебной деятельности: Кн. для учителя. — М.: Просвеще­ние, 1990. - 126 с.

58.Жлуктенко В. І., Наконечний С. І. Теорія ймовірностей і математична статис­тика: Навч.-метод, посіб. — К.: КНЕУ, 2002. — 303 с

59.Зак А. З, Как определить уровень развития мышления школьника. — М.: Знание. - 1982. - 96 с,

60.Избранные вопросы математики: 9 кл. Факультативный курс / Сост.: О. А. Бо-ковнев, В. В. Фирсов, С. И. Шварцбурд. — М.: Просвещение, 1979. — 191 с.

61.Кабанова Г. И. Мой опыт изготовления и применения пособий по геометрии. — М.: Учпедгиз, 1958. - 160 с.

62.Калмыкова 3. И. Продуктивное мышление как основа обучаемости. — М.: Педагогика, 1981. - 200 с.

63.Калмыкова 3. И. Психологические принципы развивающего обучения. — М.: Знание, 1979. - 48 с.

64.Карнацевич Л. С, Мартынова М. П., Неменко В. М. Кабинет математики в школе. — К.: Рад. шк., 1978. — 127 с.

65.Карнацевич Л. С. Уроки геометрии в 9 классе. — К.: Рад. шк., 1979. — 167 с.

66.Метельский Н. В. Дидактика математики. — Минск: Изд-во Белорус, ун-та, 1982. - 256 с.

67.Методика викладання математики: Практикум / За ред. Г. П. Бевза. — К.: Вища шк. Головне вид-во, 1981. — 199 с.

68.Методика викладання математики: Наук.-метод, зб. / За ред. І. Є.

69.Методика преподавания математики в средней школе: Общая методика / В. А. Оганесян, ІО. М. Колягин, Г. Я. Луканкин, В. Я. Соминський. — 2-е изд., перераб. и доп. — М.: Просвещение, 1980.- 367 с.

70.Слєпкань З.І. Методика навчання математики. К.: «Вища школа»,2006.

Похожие работы

Формування геометричних понять у молодших школярів

Скачать

59323

2

1

... сприймали готові образи, що їх дає вчитель, а й самі відтворювали геометричні форми в процесі моделювання, креслення, вирізування, малювання. Тому центральне місце у формуванні геометричних понять займає практика самих школярів. Сприймання простору передбачає сприймання відстані, на якій предмети розміщені від нас і один від одного, напряму, в якому вони перебувають, величини та форми предметів. ...

Методика проведення лабораторних занять з курсу "Застосування ІКТ у навчальному процесі з математики"

Скачать

111999

3

53

... може бути компетентною або некомпетентною в певних питаннях, тобто мати компетентність (компетентності) у певній галузі діяльності. Саме тому, одним із результатів навчання курсу «Застосування ІКТ у навчальному процесі з математики» вбачається формування в майбутніх вчителів відповідних ключових фахових компетентностей. Зазначене вище наштовхнуло на дослідження компетентностей: внаслідок чого ...

Активізація пізнавальної діяльності учнів в процесі навчання математики

Скачать

198737

17

8

... у фінансовій сфері. Таке означення показує, що ці задачі можуть використовуватися протягом всього учбового процесу. Останнім часом посилився пошук шляхів активізації пізнавальної діяльності учнів у процесі навчання математики за допомогою задач. Введення математичних задач фінансового змісту в шкільний курс ґрунтується на засадах та принципах процесу активізації пізнавальної діяльності учнів. ...

Використання навчальних комп’ютерних ігор в процесі вивчення математики в початковій школі

Скачать

77535

1

6

... . В ході нашого дослідження ми також виконали поставлені нами завдання. Вивчення психолого-педагогічних, а також і методичних аспектів використання комп’ютерних ігор у процесі навчання молодших школярів на уроках математики дало змогу проаналізувати шляхи такого використання, на основі чого створити свої. Підбір навчальних ігор для уроків математики в початковій школі дав змогу зробити певні на