Задача визначення — в короткій формі зафіксувати здобуті знання про предмет або явище

2.  Задача визначення — в короткій формі зафіксувати здобуті знання про предмет або явище.

3.  Визначення поняття не є раз і назавжди дане, незмінне. У міру розвитку науки заглиблюються наші знання про природу і відповідно до цього уточнюється зміст понять, а разом з цим і їх визначення. На цьому питанні ми ще зупинятимемося докладніше у зв'язку з розглядом питання про розвиток понять в науці.

4. Слід завжди мати у вигляді, що формально-логічна операція визначення поняття може бути застосована лише тоді, коли з'ясовано, що слід вважати істотним, єством. Питання ж про єство розробляє змістовна діалектична логіка.

Визначення понять з переходом учнів з класу в клас уточнюються. Це питання також розглядатиметься більш детально у зв'язку з аналізом процесу формування понять у школярів. Разом з тим вже зараз хотілося б попередити про доцільність прагнення неодмінно давати визначення поняття на самому початку його формування у школярів. У зв'язку з цим корисно привести вислів російського педагога Ц. І. Балмлона, який в книзі «Виховне читання», виданої в 1908 р., абсолютно правильно попереджав, що розвиток відвернутого понятійного мислення в дитячому віці вимагає від вчителя найбільшого терпіння і обережності; воно досягається поволі, поступово, у зв'язку з органічним зростанням дітей і накопиченням у них реального досвіду.

Відвернуті поняття повинні складатися і зростати як результат поступового розширення кругозору.

Російський педагог В. И. Шереметовский розглядав як злочин проти першої заповіді дидактики, що наказувала помірність і акуратність, прагнення вичерпувати все відразу до дна. Насправді ж всяке теоретичне положення, всякий висновок і узагальнення на перший раз відкладається, так би мовити, на поверхні свідомості, і лише при подальшому неодноразовому вживанні теорії до практики, при підкріпленні одного теоретичного положення іншим, поступово первинне поверхневе уявлення проникає в глибінь свідомості і утворюється, нарешті, той «розумовий осад», який вже можна вважати, а ясне поняття, за точне грунтовне знання.

Але з цього правильного положення про те, що для ряду понять не можна дати відразу закінченого визначення, що поняття повинні розвиватися поступово і згідно з цим на різних татах навчання повинне вводитися різне формулювання визначення, що поступово розкриває все більш і більш глибокий зміст даного поняття, зовсім не витікає, що взагалі можна не давати в процесі навчання (в підручниках) закінчених формулювань визначень ряду основних понять.

1.8. Способи означення понять.

Логіка указує прийоми визначення понять, що дозволяють розкрити істотні ознаки, не вдаючись до докладного переліку всіх істотних ознак. Є декілька способів визначення понять. Основними з них є: визначення через найближчий рід і видову відмінність, генетичне визначення — визначення через вказівку способу утворення предмету.

Виділяють також номінальне визначення — пояснення значення слова, імені або терміну, що позначає дане поняття. Є різні способи означування понять. Основний з них — через найближчий рід і видову відмінність. Наприклад, «Медіана є відрізок, що з'єднує вер­шину трикутника з серединою протилежної сторони». Тут вказано родове поняття (відрізок) і видова відмінність (з'єднує вершину з серединою протилежної сторони).Означення через абстракцію — це означення, в якому властивості множин розкриваються через відношення рівності між ними. Наприклад: «число (кардинальне) класу а є клас всіх класів, що перебувають у відношенні взаємно однозначної відповідності з класом а».

Аксіоматичне означення — це логічна операція опосередкованого розкриття змісту поняття за допомогою певної аксіоматики. Так, система аксіом геометрії Гільберта непрямо означає поняття «точка», «пряма», «площина», «належність», «між», «конгруентність». Наприклад, аксіо­ми інцидентності (належності): 1) двом точкам належить тільки одна пряма; 2) якщо дві точки прямої належать пло­щині, то й ця пряма інцидентна даній площині, опосередко­вано розкривають зміст понять «пряма», «площина», «інци­дентиність».

Оскільки зміст кожного поняття розкривається через означені вже поняття, то в процесі такого поступового зве­дення (редукції) приходять до ряду не означуваних понять. Це є первісні, основні поняття, такі як: «множина», «відпо­відність», «натуральне число», «точка», «пряма», «площина», «конгруентність» тощо.

При означуванні понять треба запобігати створен­ню сурогатів-означень, в яких за означення беруться пе­релік тих моментів з практики, які привели до утворення даного поняття. Наприклад: «Число є результат рахунку або вимірювання»; «відношення є результат порівнюван­ня» і т. д. Тут за означення поняття взято деякий його опис. Означення, по можливості, не повинно подаватися в не­гативній формі. Наприклад, означення: «трапеція не є пара­лелограм», або «ірраціональне число — це не ціле число» є неправильними.

Перший основний спосіб означення починається з вказівки роду, в який як вигляд входить визначуване поняття. При цьому береться не перший рід, що попався, а найближчий, в який даний вигляд входить. Родове поняття — це і є більш широке поняття, під яке, «підводиться» визначуване видове поняття.

Знаходження більш широкого поняття є тільки початком визначення поняття. Другий етап — вказівка видової відмінності визначуваного поняття. В кожний рід входить багато видів. Для того, щоб точно визначити поняття, треба знайти зміст даного вигляду, знайти ту специфічну істотну ознаку, по якій даний вигляд відрізняється від всієї решти видів, що входять у вказаний рід.

Вперше наукове формулювання прийому визначення поняття через найближчий рід і видову відмінність дав Арістотель. Він сформулював також правила визначення, прийняті сучасною традиційною логікою. Д. Маркс, Ф.Энгельс в своїх працях широко користувалися цим прийомом визначення поняття. Серед помилок більш типовими при означуванні є: не називання окремих істотних ознак поняття. Наприклад: «Кут, утворений двома хордами, називається вписаним» (не сказа­но, що його вершина лежить на колі); «Піраміда, в основі якої лежить правильний многокутник, називається правиль­ною» (не зазначено, що її вершина ортогонально проектується в центр основи) і т. д. Причиною таких неточних формулю­вань є недостатнє розуміння кожної з істотних ознак озна­чуваного поняття. Тому при введенні поняття слід виділяти всі їх істотні ознаки, перелічити ці ознаки, зіставити озна­чуване поняття із спорідненими, але відмінними поняттями. і називання зайвих (вивідних) ознак поняття, наприклад: «Середньою лінією трапеції називається відрізок, що сполу­чає середини бічних сторін трапеції і паралельний основам трапеції». Такі помилки є менш істотними, ніж попередні. Однак вони свідчать про те, що учні не усвідомлюють потре­би мінімалізації ознак в означенні поняття. Виправляючи їх, треба пояснити учневі, що вивідні ознаки понять є предметом не означень, а теорем; що цим демонструється не «обширність» його знань, а логічна нечіткість. Причиною таких помилок є дещо неосмислене нагромадження учнем ряду споріднених фактів. Щоб запобігти появі таких поми­лок, доцільно в ході викладання та після розгляду певної теми (наприклад, про трапецію) показ учням логічне при­значення кожного із розглянутих математичних тверджень.

Називання суперечних ознак, наприклад, «Паралело­грам — це чотирикутник, у якого протилежні сторони по­парно паралельні, а кути діагоналями поділяються навпіл». У подібних випадках пояснюємо, що не можна об'єднувати в одному твердженні істотні ознаки поняття загального виду із специфічними ознаками підпорядкованого йому поняття.

Похожие работы

Формування геометричних понять у молодших школярів

Скачать

59323

2

1

... сприймали готові образи, що їх дає вчитель, а й самі відтворювали геометричні форми в процесі моделювання, креслення, вирізування, малювання. Тому центральне місце у формуванні геометричних понять займає практика самих школярів. Сприймання простору передбачає сприймання відстані, на якій предмети розміщені від нас і один від одного, напряму, в якому вони перебувають, величини та форми предметів. ...

Методика проведення лабораторних занять з курсу "Застосування ІКТ у навчальному процесі з математики"

Скачать

111999

3

53

... може бути компетентною або некомпетентною в певних питаннях, тобто мати компетентність (компетентності) у певній галузі діяльності. Саме тому, одним із результатів навчання курсу «Застосування ІКТ у навчальному процесі з математики» вбачається формування в майбутніх вчителів відповідних ключових фахових компетентностей. Зазначене вище наштовхнуло на дослідження компетентностей: внаслідок чого ...

Активізація пізнавальної діяльності учнів в процесі навчання математики

Скачать

198737

17

8

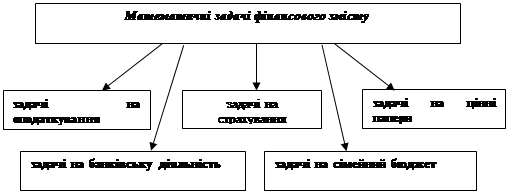
... у фінансовій сфері. Таке означення показує, що ці задачі можуть використовуватися протягом всього учбового процесу. Останнім часом посилився пошук шляхів активізації пізнавальної діяльності учнів у процесі навчання математики за допомогою задач. Введення математичних задач фінансового змісту в шкільний курс ґрунтується на засадах та принципах процесу активізації пізнавальної діяльності учнів. ...

Використання навчальних комп’ютерних ігор в процесі вивчення математики в початковій школі

Скачать

77535

1

6

... . В ході нашого дослідження ми також виконали поставлені нами завдання. Вивчення психолого-педагогічних, а також і методичних аспектів використання комп’ютерних ігор у процесі навчання молодших школярів на уроках математики дало змогу проаналізувати шляхи такого використання, на основі чого створити свої. Підбір навчальних ігор для уроків математики в початковій школі дав змогу зробити певні на