Виды измерений и причины ошибок
Наиболее вероятное значение измеряемой величины
Понятие доверительного интервала и доверительной вероятности
Ошибки косвенных измерений
Найдем средние значения и погрешности следующих пяти измерений
Виды случайных величин и законы их распределения
Числовые характеристики случайных величин, заданных своими распределениями
Закон Пуассона
Вероятности ошибок первого и второго рода
Графический метод обработки результатов
Аналитические методы обработки результатов
Знак S обозначают сумму величин от i = 1 до i = n, где n
Номограммы в декартовой системе координат
Навигация
Аналитические методы обработки результатов
Обработка результатов экспериментов и наблюдений
87319
знаков
11
таблиц
16
изображений
3.3. Аналитические методы обработки результатов
Графический метод обработки результатов обладает наглядностью, относительной простотой, однако его результаты содержат определенную субъективность и относительно низкую точность.
Аналитические методы лишены в какой - то степени указанных недостатков и позволяют получить результат для более широкого класса функций с большей точностью, чем графический метод.
Существуют различные аналитические методы получения параметров эмпирических кривых в зависимости от критерия, принятого при их получении. Рассмотрим некоторые из существующих способов.
3.3.1. Способ средней
Допустим, что имеется n сочетаний xi, yi, полученных при эксперименте. Даже в том случае, если между х и y теоретически установлена функциональная связь ( в данном случае предположим, что линейная ), то наблюдаемые значения yi будут отличаться от ахi + b вследствие наличия экспериментальных ошибок. Обозначим через Di соответствующую ошибку
Di = yi - axi - b (i = 1, 2, ..., n)
Если выбирать параметры а и b так, чтобы для всех n наблюдений ошибки уравновешивались, т.е.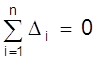 
, то это привело бы нас к одному уравнению, тогда как для нахождения двух коэффициентов (а, b) их требуется два. Поэтому предположим, что уравновешивание происходит не только для всех произведенных наблюдений в целом, но и для каждой группы, содержащей половину ( или почти половину ) всех наблюдений в отдельности.
В этом случае можно прийти к системе уравнений
,
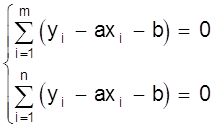где m - число наблюдений в первой группе.
Данную систему уравнений запишем теперь в виде
.
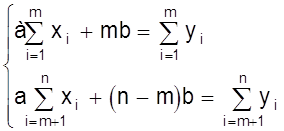Изложенное показывает, что метод средних ²уравновешивает² положительные и отрицательные отклонения теоретической кривой от экспериментальных значений.
Пример.Используя данные рис. 10 определим коэффициенты а, b методом средней. Для этого семь измерений разделим на две группы m = 3 первых значений, n - m = 4 последующих
; 
;
; 
.
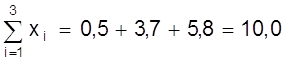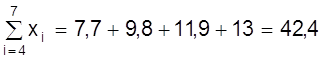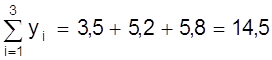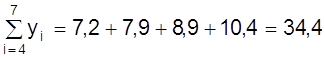Получаем систему
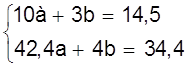
Решая систему находим
;
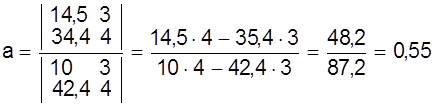b =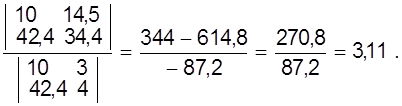 
Таким образом способ средней дает прямую
y = 0,55х + 3,11.
В сравнении с графическим способом коэффициенты а совпадают и имеется различие в коэффициенте b.
3.3.2. Метод наименьших квадратов
В методе средних при определении коэффициентов уравнения использовалось условие равенства нулю алгебраической суммы отклонений результатов эксперимента от теоретической кривой ( в частном случае прямой ). Очевидно, что при этом Di могут быть значительной величины. Имеет значение только ²уравновешивание² положительных и отрицательных отклонений.
Поставим теперь задачу нахождения по результатам наблюдений наиболее вероятные значения неизвестных коэффициентов.
Предположим, что искомая зависимость y = ¦(х) существует. Тогда параметры этой линии необходимо выбрать таким образом, чтобы точки yi располагались по обе стороны кривой y = ¦(х) как можно ближе к последней. Предположим, что разброс точек yi относительно y = ¦(х) подчиняется закону нормального распределения. Тогда мерой разброса является дисперсия s2 или ее приближенное выражение - средний квадрат отклонений.
.
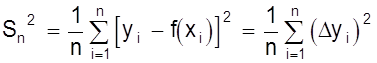И требование минимального разброса будет удовлетворено, если минимизировать выражение ( Dyi )2. Как известно, необходимым условием того, что функция приобретает минимальное значение, является то, что ее первая производная ( или частные производные для функции многих переменных ) равна нулю. Применение метода наименьших квадратов имеет смысл, если число экспериментальных точек n больше числа определяемых коэффициентов.
Рассмотрим реализацию метода наименьших квадратов применительно к уравнению вида y = ax + b.
Для нахождения коэффициентов а, b искомой прямой необходимо минимизировать сумму квадратов расстояний Dyi по ординате от точки (хi; yi) до прямой ( см. рис. 12 ). Расстояния Dyi определятся
Dyi = yi - axi - b.
Рис. 12. К способу наименьших квадратов
Для минимизации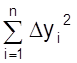 
приравниваем к нулю производные этой суммы по параметрам а, b:
;
.
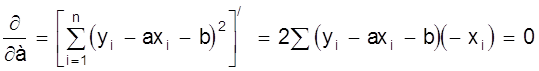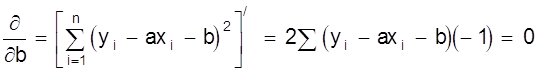Преобразуем эту систему
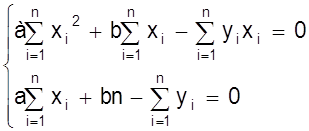
Получим систему нормальных уравнений метода наименьших квадратов.
Решая ее относительно а, b получаем:
; 
.
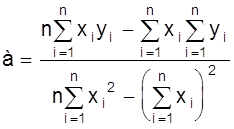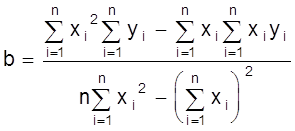Вычисляя из n опытов необходимые суммы и производя указанные действия, получаем величину коэффициентов а, b.
Как видно, способ наименьших квадратов достаточно громоздок и при его применении широко используется вычислительная техника. Метод наименьших квадратов может использоваться и в случае нелинейных функций. Например, если определяются параметры квадратичной зависимости:
y = ах2 + bx + с,
то
.
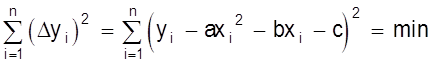Дифференцируя это соотношение по а, b, с получаем систему нормальных уравнений:
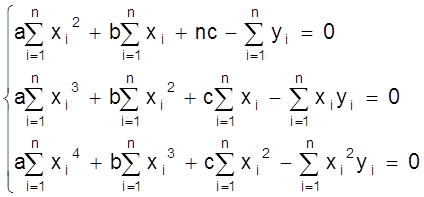
Из этой системы можно определить параметры а, b, с.
При использовании метода наименьших квадратов при других нелинейностях, удобнее будет линеаризовать исходные зависимости.
В табл. 4 приведены системы нормальных уравнений для некоторых исходных уравнений.
Таблица 4
Системы нормальных уравнений
| Исходное уравнение | Система нормальных уравнений |
| y=axb |
|
| y=a×lgx+b |
|
| y=eax+b |
|
| y=aebx |
|
| y= |
|
| y= |
|
| y= |
|
Примечания: 1. Величины х, y обозначают значения величин хi, yi в i-ом
опыте;
Похожие работы
... Как видно, с ростом числа измерений различие между результатами, вычислениями по распределению Стьюдента и по нормальному распределению уменьшается. Контрольные вопросы Цель математической обработки результатов эксперимента; Виды измерений; Типы ошибок измерения; Свойства случайных ошибок; Почему среднеарифметическое значение случайной величины при нормальном законе ее распределения является ...
... распределения случайной величины. а) коэффициент асимметрии; б) момент случайной величины; в) коэффициент эксцесса; г) математическое ожидание. Ответ: в). Тема 9. МЕТОДЫ ВТОРИЧНОЙ СТАТИСТИЧЕСКОЙ ОБРАБОТКИ РЕЗУЛЬТАТОВ ПЕДАГОГИЧЕСКОГО ЭКСПЕРИМЕНТА Тестовое задание 1. Выберите верные ответы. В зависимости от используемых источников информации исследования делятся на: а) кабинетные; б) ...
... , казалось бы, характеризуется чисто эмпирическими признаками: изменением управляемых условий, включением и выключением приборов и различных механизмов, фиксированием тех или иных свойств, эффектов и т. п. В ходе эксперимента как бы уменьшается роль теории. Но на самом деле наоборот - без теоретического знания невозможны постановка промежуточных задач и их решение. Экспериментальная установка - ...
... свободы остается на проверку гипотезы адекватности. Если заранее пренебречь взаимодействиями высших порядков, то имеется возможность получить математическую модель при меньшем числу опытов, реализовав не весь план ДФЭ, а только его часть (дробную реплику). Эксперимент, реализующий часть (дробную реплику) полного факторного эксперимента, называется дробным факторным экспериментом (ДФЭ). ДФЭ ...
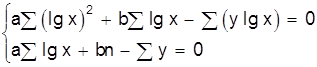
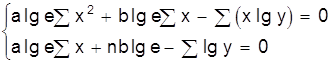
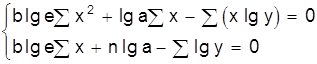
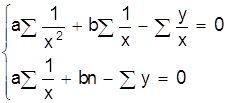
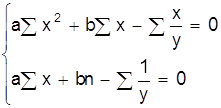
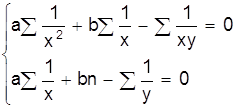
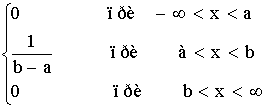
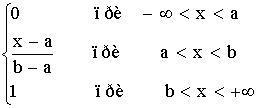
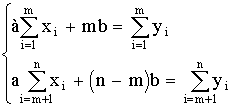
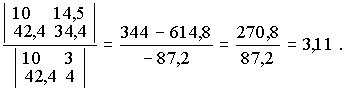
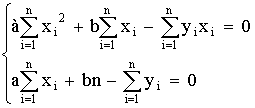
0 комментариев