Виды измерений и причины ошибок
Наиболее вероятное значение измеряемой величины
Понятие доверительного интервала и доверительной вероятности
Ошибки косвенных измерений
Найдем средние значения и погрешности следующих пяти измерений
Виды случайных величин и законы их распределения
Числовые характеристики случайных величин, заданных своими распределениями
Закон Пуассона
Вероятности ошибок первого и второго рода
Графический метод обработки результатов
Аналитические методы обработки результатов
Знак S обозначают сумму величин от i = 1 до i = n, где n
Номограммы в декартовой системе координат
Навигация
Наиболее вероятное значение измеряемой величины
Обработка результатов экспериментов и наблюдений
87319
знаков
11
таблиц
16
изображений
1.5. Наиболее вероятное значение измеряемой величины
Допустим, что для определения истинного значения Х измеряемой величины было сделано n равноточных измерений с результатами а1, а2.. .аn. Естественно, что ряд этих чисел будет больше Х, другие меньше Х и неясно, какое из этих чисел ближе всего подходит к Х.
Представим результаты измерений в виде очевидных равенств:
а1 = Х - Dх1; а2 = Х - Dх2; ... ; аn = Х - Dхn.
Естественно, что истинные абсолютные ошибки Dхi могут принимать как положительные, так и отрицательные значения.
Суммируя левые и правые стороны равенств получим
.
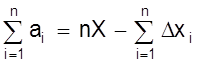Поделим обе части равенства на число измерений n и получим
.
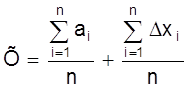Величина
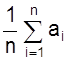является среднеарифметическим величины Х. Если число n достаточно велико ( при n®¥), то согласно четвертому свойству случайных ошибок
.
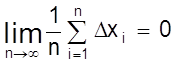Это же видно и по кривой Гаусса (рис. 1), где всякой положительной погрешности соответствует равная ей отрицательная.
Из изложенного следует, что
Х = а при n ® ¥,
т.е. при бесконечном числе измерений истинное значение измеряемой величины равно среднеарифметическому значению результатов всех измерений. При ограниченном числе измерений истинное значение будет отличаться от среднеарифметического и необходимо оценить величину этого расхождения: Х = а ± Dх.
Следует еще раз подчеркнуть, что среднеарифметическое значение, принимаемое за истинное значение измеряемой величины, является наиболее вероятным значением. Среди значений аiмогут оказаться значения, которые в действительности ближе к истинному значению.
Отклонение Dх вероятнейшего значения а от его истинного значения Х называют истинной абсолютной ошибкой.
1.6. Оценка точности измерений
Для ряда равноточных измерений а1, а2 ...аn определим его среднеарифметическое значение а и составим разности (а - а1), (а - а2), ..., (а - аn).
Каждую из этих разностей называют вероятнейшей ошибкой отдельного измерения (Vi). Вероятнейшие ошибки, как и истинные ошибки Dхi = (Х - аi), бывают положительные и отрицательные, нулевые. Рассмотрим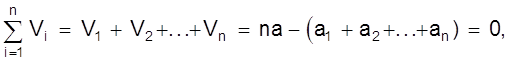 
т.е. алгебраическая сумма вероятнейших ошибок равна нулю при любом числе измерений. Истинные случайные ошибки таким свойством не обладают.
Вероятнейшие ошибки Vi лежат в основе математической обработки результатов измерений: именно по ним вычисляют предельную абсолютную ошибку Dаi среднеарифметического а и тем самым оценивают точность результата измерений.
Средняя истинная случайная ошибка (иначе - среднее отклонение отдельного измерения) определяется выражением (Dх1+Dх2+...+Dхn)/n.
Величина [(Dх1)2+(Dх2)2+...+(Dхn)2]/n представляет средний квадрат случайной ошибки или дисперсию S2 выборки (при ограниченном n) или генеральной совокупности s2 (при бесконечном n). Средняя квадратичная ошибка отдельного измерения S =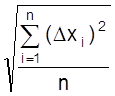 
является лучшим критерием точности, чем средняя случайная ошибка, т.к. не происходит компенсации положительных и отрицательных ошибок Dхi и сильнее учитывается действие крупных ошибок.
Поскольку истинное значение Х измеряемой величины неизвестно, то неизвестны и истинные случайные ошибки 
хi. Для определения средней квадратичной ошибки S используется положение теории случайных ошибок, что при большом числе измерений n справедливо равенство
.
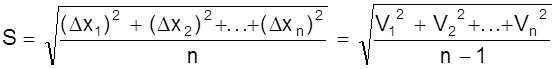Различный знаменатель объясняется тем, что величины хi являются независимыми, а из n величин Vi независимыми являются n-1, т.к. в величину Vi входит а, само определяемое из этих же n измерений.
Важно, что не зная самих истинных случайных ошибок удается вычислить среднюю квадратичную ошибку определенного измерения:
S = ±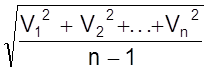
.
Оценим теперь погрешность результата всей серии эксперимента, т.е. определим величину Dх = Х - а.
Для этого проведем преобразование выражения
Sn2 =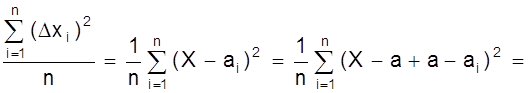 
= 
= 
.
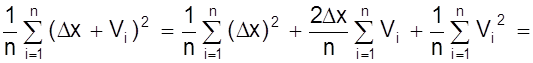
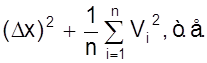
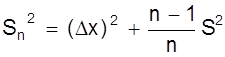Если
повторить серии по n измерений в каждой N ðàç, ìîæíî ïîëó÷ить средние значения а1, а2, ... , аN и погрешности результатов измерений
(Dх)1 = (Х - а1); (Dх)2 = (Х - а2); ... ; (Dх)N = (Х - аN)
и среднюю среднеквадратичную погрешность серии
Sa2 =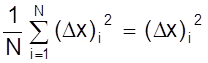 
.
При большом числе N S2a ® s2a
.
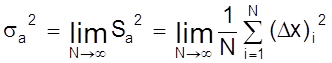Усредняя выражение S2n по числу серий N, получаем
Sa2 = (Dx)2 = Sn2 -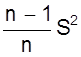 
.
Учитывая что при большом n S2n ® s2 и S2 ® s2 получаем искомую
связь между дисперсиями всего опыта s2a и отдельного эксперимента [i1] s2
,
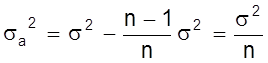т.е. дисперсия s2a результата серии из n измерений в n раз меньше дисперсии отдельного измерения. При ограниченном числе n измерений приближенным выражением s2a будет S2a
.
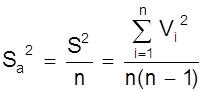Выражения s2a и S2a отражают фундаментальный закон возрастания точности при росте числа наблюдений. Из него следует, что желая повысить точность измерений в 2 раза мы должны сделать вместо одного - четыре измерения; чтобы повысить точность в 3 раза, нужно увеличить число измерений в 9 раз и т.д.
Похожие работы
... Как видно, с ростом числа измерений различие между результатами, вычислениями по распределению Стьюдента и по нормальному распределению уменьшается. Контрольные вопросы Цель математической обработки результатов эксперимента; Виды измерений; Типы ошибок измерения; Свойства случайных ошибок; Почему среднеарифметическое значение случайной величины при нормальном законе ее распределения является ...
... распределения случайной величины. а) коэффициент асимметрии; б) момент случайной величины; в) коэффициент эксцесса; г) математическое ожидание. Ответ: в). Тема 9. МЕТОДЫ ВТОРИЧНОЙ СТАТИСТИЧЕСКОЙ ОБРАБОТКИ РЕЗУЛЬТАТОВ ПЕДАГОГИЧЕСКОГО ЭКСПЕРИМЕНТА Тестовое задание 1. Выберите верные ответы. В зависимости от используемых источников информации исследования делятся на: а) кабинетные; б) ...
... , казалось бы, характеризуется чисто эмпирическими признаками: изменением управляемых условий, включением и выключением приборов и различных механизмов, фиксированием тех или иных свойств, эффектов и т. п. В ходе эксперимента как бы уменьшается роль теории. Но на самом деле наоборот - без теоретического знания невозможны постановка промежуточных задач и их решение. Экспериментальная установка - ...
... свободы остается на проверку гипотезы адекватности. Если заранее пренебречь взаимодействиями высших порядков, то имеется возможность получить математическую модель при меньшем числу опытов, реализовав не весь план ДФЭ, а только его часть (дробную реплику). Эксперимент, реализующий часть (дробную реплику) полного факторного эксперимента, называется дробным факторным экспериментом (ДФЭ). ДФЭ ...
0 комментариев