Навигация
Знак S обозначают сумму величин от i = 1 до i = n, где n
2. Знак S обозначают сумму величин от i = 1 до i = n, где n
- число равноточных измерений.
3.3.3. Интерполирование функций
Известно, что под интерполированием понимают отыскание значений функции, соответствующих промежуточным значениям аргумента, отсутствующим в таблице логарифмов, тригонометрических и др. функций.
В общем смысле можно сказать, что задача интерполирования обратна задаче табулирования функций. При интерполировании по таблице значений функции строится ее аналитическое выражение, т.е. по значениям функции yo, y1, ..., yn при значениях аргумента хо, х1, ..., хn определяется выражение неизвестной функции.
Понятно, что через данные точки ( даже большого числа ) можно провести множество различных кривых. Поэтому существует интерполирование в различных функциях F (х). Чаще всего требуют, чтобы функция F(х) была многочленом степени на единицу меньшей, чем число известных значений.
Таким образом, задачу интерполирования функций можно сформулировать следующим образом.
Для данных значений х º хо, х1, ..., хn и y º yo, y1, ..., yn найти многочлен y = F (х) степени n, удовлетворяющий условиям F (хо) = yo, F (х1) = y1, ..., F (хn) = yn. Точки хо, х1, ..., хn называют узлами интерполяции. Многочлен F (х) - интерполяционным многочленом , а формулы его построения - интерполяционными формулами.
Как видно из описания сущности интерполирования, в отличии от описанных ранее способов получения функций ( графического, метода средних, метода наименьших квадратов ), интерполяционный многочлен опишет кривую, проходящую точно через заданные точки.
3.3.4. Параболическое интерполирование
При параболическом интерполировании в качестве интерполяционного многочлена F (х) принимают многочлен n - ой степени вида
F (х) = ао + а1х + а2х2 + ... + аnxn.
Используя свойство прохождения функции F (х) через заданные точки для неизвестных коэффициентов аi можно составить n + 1 уравнений с n + 1 неизвестным:
ао + а1хо + а2хо2 + ... + аnхоn = yo;
ао + а1х1 + а2х12 + ... + аnх12 = y1;
....................................................
ао + а1хn + а2хn2 + ... + аnхn2 = yn.
Эта система имеет единственное решение, если значения хi отличны друг от друга. Понятно, что при большом n возникает сложность решения этой системы. Перед рассмотрением общего способа решения, рассмотрим простой пример.
Дано: хо = 0, х1 = 1, х2 = 2, yо = 1, y1 = 1, y2 = 3. Определить многочлен F (х).
Записывая многочлен F (х) в виде
F (х) = ао + а1х + а2х2
составим систему уравнений
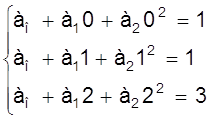 или
или 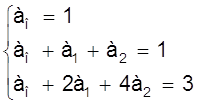
откуда ао = 1, а1 = - 1, а2 = 1 и интерполирующий многочлен имеет вид
F (х) = 1 - х + х2.
Теперь рассмотрим общий подход к отысканию интерполяционного многочлена F (х), не решением системы, а непосредственной записью.
Определим выражение для многочлена, принимающего в точке х = хо значение yо = 1, а в точках х = х1, х2, ..., хn - значения y1 = y2 = ... = yn = 0. Очевидно, что многочлен будет иметь вид
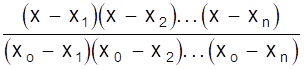 .
.
Здесь при х = хо числитель и знаменатель равны, а при х = х1, х2, ..., хn - числитель равен нулю.
Теперь построим многочлен Fо (х), принимающий в точке хо значение yо и обращающийся в нуль для значений х = х1, х2, ..., хn. Учитывая предыдущее построение можно записать
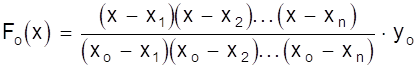 .
.
Теперь можно записать многочлен F (х) для произвольного значения хi ( i = 0, 1, 2, ..., n ) принимающего значения F (хi) = yi, а во всех остальных точках х ¹ хi значение, равное нулю
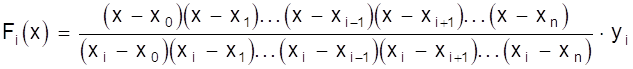 .
.
Как видно из записи, числитель не будет содержать выражения (х - хi), а знаменатель - (хi - хi), т.е. выражений, обращающих числитель и знаменатель в нуль.
Искомый многочлен будет равен сумме
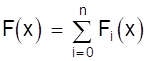 ,
,
т.е. снова в каждой точке хi одно из слагаемых принимает нужное значение yi, а все остальные обращаются в нуль.
В развернутом виде
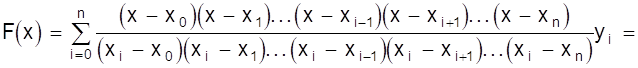
=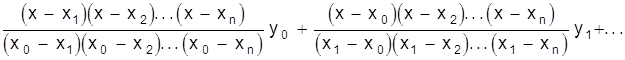
... + 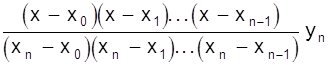 .
.
Полученная формула называется интерполяционной формулой Лагранжа.
Используя формулу Лагранжа запишем многочлен F (х) для разобранного выше примера.
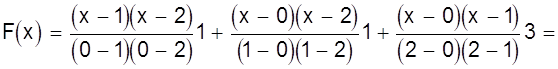
= 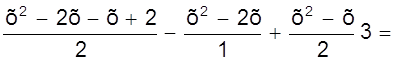
=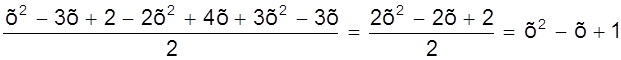 .
.
Получили тоже самое выражение, что и ранее.
Контрольные вопросы
1. Назначение графического метода обработки результатов;
2. Сущность графического метода обработки результатов;
3. Понятие и назначение функциональной шкалы;
4. Выбор масштаба функциональной шкалы;
5. Сущность аппроксимации методом средних;
6. Сущность аппроксимации методом наименьших квадратов;
7. Принципиальное отличие метода интерполирования от метода наименьших квадратов.
4.ОСНОВЫ НОМОГРАФИИ
Номография - слово греческое. Номос - закон, графо - пишу, черчу. В буквальном переводе это слово означает ²черчение закона².
Своей задачей номография ставит построение специальных графиков - номограмм, служащих для решения различных уравнений. Номограммы дают возможность компактно представлять функции многих переменных и таблицы с несколькими входами. На номограммах можно решать некоторые трансцендентные уравнения и системы таких уравнений. Номограммы можно применять не только для вычислительных целей, но и для исследования положенных в их основу функциональных зависимостей.
Наглядность представления различных закономерностей и простота использования номограмм при достаточно высокой точности результата обеспечивают широкое использование номограмм в различных областях техники.
В основе номограмм лежит понятие функциональной шкалы ( см. выше ). На основе функциональных шкал создаются не только номограммы, но и различные вычислительные средства: универсальные вычислительные номограммы, логарифмические линейки и т.п.
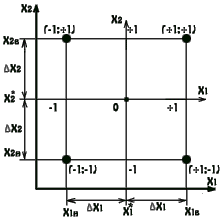
В данной главе излагается один из возможных видов номограмм - номограммы в декартовой системе координат, имеющие достаточно широкое использование в машиностроении.
Похожие работы
... Как видно, с ростом числа измерений различие между результатами, вычислениями по распределению Стьюдента и по нормальному распределению уменьшается. Контрольные вопросы Цель математической обработки результатов эксперимента; Виды измерений; Типы ошибок измерения; Свойства случайных ошибок; Почему среднеарифметическое значение случайной величины при нормальном законе ее распределения является ...
... распределения случайной величины. а) коэффициент асимметрии; б) момент случайной величины; в) коэффициент эксцесса; г) математическое ожидание. Ответ: в). Тема 9. МЕТОДЫ ВТОРИЧНОЙ СТАТИСТИЧЕСКОЙ ОБРАБОТКИ РЕЗУЛЬТАТОВ ПЕДАГОГИЧЕСКОГО ЭКСПЕРИМЕНТА Тестовое задание 1. Выберите верные ответы. В зависимости от используемых источников информации исследования делятся на: а) кабинетные; б) ...
... , казалось бы, характеризуется чисто эмпирическими признаками: изменением управляемых условий, включением и выключением приборов и различных механизмов, фиксированием тех или иных свойств, эффектов и т. п. В ходе эксперимента как бы уменьшается роль теории. Но на самом деле наоборот - без теоретического знания невозможны постановка промежуточных задач и их решение. Экспериментальная установка - ...
... свободы остается на проверку гипотезы адекватности. Если заранее пренебречь взаимодействиями высших порядков, то имеется возможность получить математическую модель при меньшем числу опытов, реализовав не весь план ДФЭ, а только его часть (дробную реплику). Эксперимент, реализующий часть (дробную реплику) полного факторного эксперимента, называется дробным факторным экспериментом (ДФЭ). ДФЭ ...
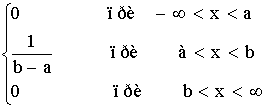
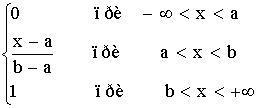
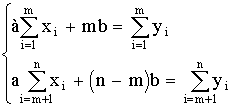
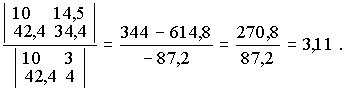
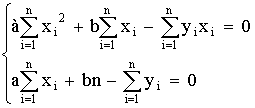
0 комментариев