Навигация
Ошибки косвенных измерений
1.9. Ошибки косвенных измерений
Часто измеряется не непосредственно интересующая нас величина, а другая, зависящая от нее некоторым образом. Например, при резании металлов часто непосредственно измеряются деформации, ЭДС, по которым судят о возникающих силах и температурах. При этом также необходимо оценить ошибку измерения.
При косвенных измерениях значение y измеряемой величины находят по некоторой формуле
y = ¦ (х1, х2, ... , хm),
где x1, x2, ... xm - средние арифметические измеряемые (непосредственно) величины. Рассмотрим функцию общего вида
y = ¦ (х1, х2, ... , хm)
где x1, x2, ... , xm - независимые переменные, для определения которых производятся n прямых независимых измерений по каждой xi.
Обозначим значения переменных через среднее значение и отклонения
y ± Dy = ¦ (x1 ± Dx1, x2 ± Dx2, ... , xm ± Dxm).
Эту функцию представим рядом Тейлора, ограничив его первыми членами ряда ( принимая Dxi << xi )
y ± Dy = ¦(х1, х2, ... , хn) ± 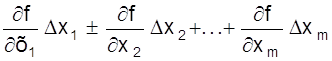 ,
,![]()
где
![]() - производная функции по xi, взятая в точке xi.
- производная функции по xi, взятая в точке xi.
Учитывая, что y = ¦ (x1, x2, ... , xm) получаем
Dy = 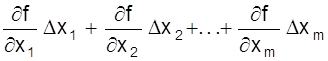 .
.
Чтобы учесть погрешности Dxi всех n опытов целесообразно использовать средние квадратические оценки ( D xi)2, так как Dxi = 0.
Возведем в квадрат левую и правую части уравнения и разделим на n
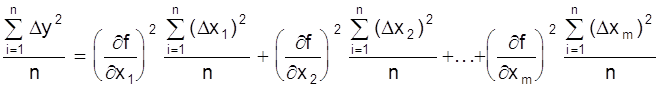 .
.
Здесь суммы удвоенных произведений типа
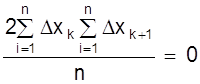
![]()
согласно четвертому свойству случайных ошибок ( Dxi = 0 ).
Тогда в левой и правой частях имеем среднеквадратические погрешности функции и аргументов
S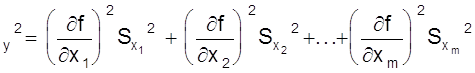 .
.
Пример. При тарировке динамометра было получено уравнение зависимости силы от отклонения l луча осциллографа вида P = 25 l. Точность измерения отклонения D l = 1 мм. Тогда
DP = ![]() .
.
В качестве меры точности лучше выступает не абсолютная, а относительная погрешность.
ε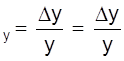 .
.
Рассмотрим ее определение на примере. Пусть
y = cx1a×x2b×x3g.
Тогда
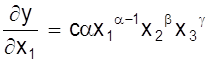 ;
; 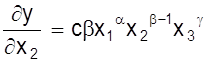 ;
;
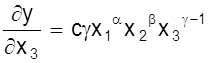 .
.
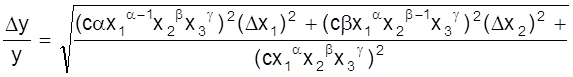
![]()
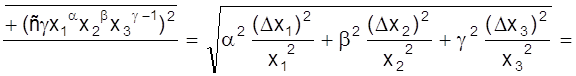
= ![]() .
.
Аналогично можно определить относительную погрешность и при других зависимостях. Зная относительную погрешность, можно определить и абсолютное ее значение:
Dy = y×εy.
1.10. Правила округления чисел
Величина погрешности результата измерений физической величины дает представление о том, какие цифры в числовом значении измеряемой величины сомнительны. Поэтому результаты измерений следует округлять перед тем, как производить с ними дальнейшие вычисления.
Округлять числовое значение результата измерений следует в соответствии с числовым разрядом значащей цифры погрешности. При этом выполняют общие правила округления.
Лишние цифры в целых числах заменяются нулями, а в десятичных дробях отбрасываются ( как и лишние нули ). Например, если погрешность измерения ± 0,001 мм, то результат 1,07005 округляется до 1,070.
Если первая из изменяемых нулями и отбрасываемых цифр меньше 5, остающиеся цифры не изменяются. Например, число 148935, точность измерения ± 50, округление: 148900.
Если первая из заменяемых нулями или отбрасываемых цифр равна 5, а за ней не следует никаких цифр или идут нули, то округление производится до ближайшего четного числа. Например, число 123,50 округляется до 124.
Если первая из заменяемых нулями или отбрасываемых цифр больше 5 или равна 5, но за ней следует значащая цифра, то последняя остающаяся цифра увеличивается на единицу. Например, число 6783,6 округляется до 6784.
1.11. Порядок обработки результатов измерений
При практической обработке результатов измерений можно последовательно выполнить следующие операции:
1. Записать результаты измерений;
2. Вычислить среднее значение из n измерений
а = 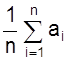
3. Определить погрешности отдельных измерений Vi = а - аi;
4. Вычислить квадраты погрешностей отдельных измерений Vi2;
5. Если несколько измерений резко отличаются по своим значениям от остальных измерений, то следует проверить не являются ли они промахом. При исключении одного или нескольких измерений п.п.1...4 повторить;
6. Определяется средняя квадратичная погрешность результата серии измерений
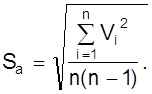
7. Задается значение надежности a;
8. Определяется коэффициент Стьюдента ta (n) для выбранной надежности a и числа проведенных измерений n;
9. Находятся границы доверительного интервала
Dх = ta(n)×Sa
10. Если величина погрешности результата измерений (п.9) окажется сравнимой с величиной d погрешности прибора, то в качестве границы доверительного интервала следует взять величину
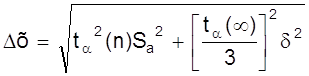 .
.
11. Записать окончательный результат
X = a ± Dx ;
12. Оценить относительную погрешность результата серии измерений
ε = 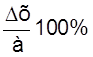 .
.![]()
1.12. Обработка результатов измерений диаметра цилиндра
Микрометром было сделано десять замеров диаметра цилиндра. Цена деления микрометра 0,01 мм. Определить диаметр цилиндра с надежностью a = 0,95 и a = 0,99. Оценить влияние числа замеров на точность получаемого результата.
аi: 14,85; 14,80; 14,84; 14,81; 14,79;
14,81; 14,80; 14,85; 14,84; 14,80.
1. Для первых пяти измерений определим среднеарифметическое значение и границы доверительного интервала. Для удобства расчетов выберем произвольное число ао удобное для расчетов (ао = 14,80 мм) и определим разности (аi - ао) и квадраты этих разностей. Результаты сведены в таблицу.
| i | аi, мм | аi - ао, мм | (аi - ао)2, мм2 |
| 1 | 14, 85 | 0, 05 | 0, 0025 |
| 2 | 14, 80 | 0, 00 | 0, 0000 |
| 3 | 14, 84 | 0, 04 | 0, 0016 |
| 4 | 14, 81 | 0, 01 | 0, 0001 |
| 5 | 14, 79 | -0, 01 | 0, 0001 |
| | 0, 09 | 0, 0043 | |
Найдем среднее значение а и среднеквадратичное отклонение Sа:
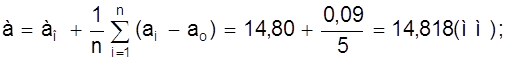
а - ао = 0, 018 мм;
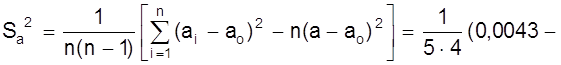
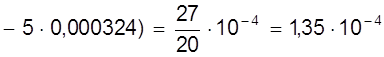
![]() ( мм2 );
( мм2 );
![]() ( мм ).
( мм ).
Для надежности a = 0,95 и n = 5 ta = 2,78. Абсолютная погрешность измерения Dх:
Dх = ta× Sа = 2,78 × 0,0116 = 0,0322 мм.
Результат измерения можно представить в виде
(14,818 - 0,032) мм £ а £ (14,818 + 0,032) мм
или сохраняя в величине погрешности одну значащую цифру
(14,82 - 0,03) мм £ а £ (14,82 + 0,03) мм,
т.е. 14,79 мм £ а £ 14,85 мм или а = (14,82 ± 0,03) мм.
Относительная погрешность
εа = 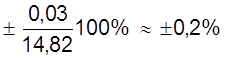 .
.
Теперь найдем абсолютную и относительную погрешность этих измерений при a = 0,99.
В этом случае ta = 4,60. Тогда
Dх = ta×Sa = 4,60×1,16×10-2 = 5,34×10-2 ( мм ).
Следовательно а = (14,82 ± 0,05) мм
εа = 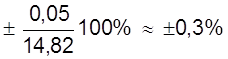 .
.
Видно, что с увеличением надежности границы доверительного интервала возросли, а точность результата уменьшилась.
2. Проведем расчет погрешностей для этих же пяти измерений, незаконно полагая, что s2 = S2n (что при n = 5 ошибочно). Для этого используем распределение Гаусса (а не Стюарта). При a = 0,95 ka = 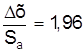 .
.
Это дает возможность определить
Dх = ka×Sa = 1,96×1,16×10-2 » 2×10-2 ( мм ),
т.е. погрешность получилась меньше примерно на 30%. Если по этой величине погрешности определить величину надежности при ta = ka, то из таблицы коэффициентов Стьюдента получим a < 0,90 вместо заданной a = 0,95. Следовательно при малом числе измерений n применение закона нормального распределения с s2 = S2n вместо распределения Стьюдента приводит к уменьшению надежности результата измерений.
Похожие работы
... Как видно, с ростом числа измерений различие между результатами, вычислениями по распределению Стьюдента и по нормальному распределению уменьшается. Контрольные вопросы Цель математической обработки результатов эксперимента; Виды измерений; Типы ошибок измерения; Свойства случайных ошибок; Почему среднеарифметическое значение случайной величины при нормальном законе ее распределения является ...
... распределения случайной величины. а) коэффициент асимметрии; б) момент случайной величины; в) коэффициент эксцесса; г) математическое ожидание. Ответ: в). Тема 9. МЕТОДЫ ВТОРИЧНОЙ СТАТИСТИЧЕСКОЙ ОБРАБОТКИ РЕЗУЛЬТАТОВ ПЕДАГОГИЧЕСКОГО ЭКСПЕРИМЕНТА Тестовое задание 1. Выберите верные ответы. В зависимости от используемых источников информации исследования делятся на: а) кабинетные; б) ...
... , казалось бы, характеризуется чисто эмпирическими признаками: изменением управляемых условий, включением и выключением приборов и различных механизмов, фиксированием тех или иных свойств, эффектов и т. п. В ходе эксперимента как бы уменьшается роль теории. Но на самом деле наоборот - без теоретического знания невозможны постановка промежуточных задач и их решение. Экспериментальная установка - ...
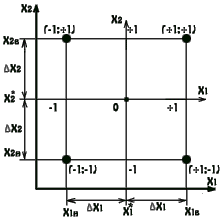
... свободы остается на проверку гипотезы адекватности. Если заранее пренебречь взаимодействиями высших порядков, то имеется возможность получить математическую модель при меньшем числу опытов, реализовав не весь план ДФЭ, а только его часть (дробную реплику). Эксперимент, реализующий часть (дробную реплику) полного факторного эксперимента, называется дробным факторным экспериментом (ДФЭ). ДФЭ ...
0 комментариев