Решение иррациональных неравенств, способом введения новой переменной

8. Решение иррациональных неравенств, способом введения новой переменной.

Иррациональные неравенства, как и иррациональные уравнения можно решать способом введения новой переменной. Рассмотрим использование этого метода на примерах.

Пример 1. Решить неравенство:

Решение. Положив , находим что х² + 5х + 4 = у² – 24, тогда неравенство (1) преобразуется к виду:

у² – 5y – 24 < 0

и далее решим уравнение:

у² – 5y – 24 = 0

D = 25 + 96 = 121

y₁ = -3, y₂ = 8

получаем (у – 8)(у + 3) < 0.

Решением этого неравенства является промежуток -3 < y < 8.

Мы пришли к следующей системе неравенств:

Так как при всех допустимых значениях х, то тем более при всех х их ОДЗ неравенства (1), а поэтому достаточно решить неравенство:

Это неравенство равносильно системе

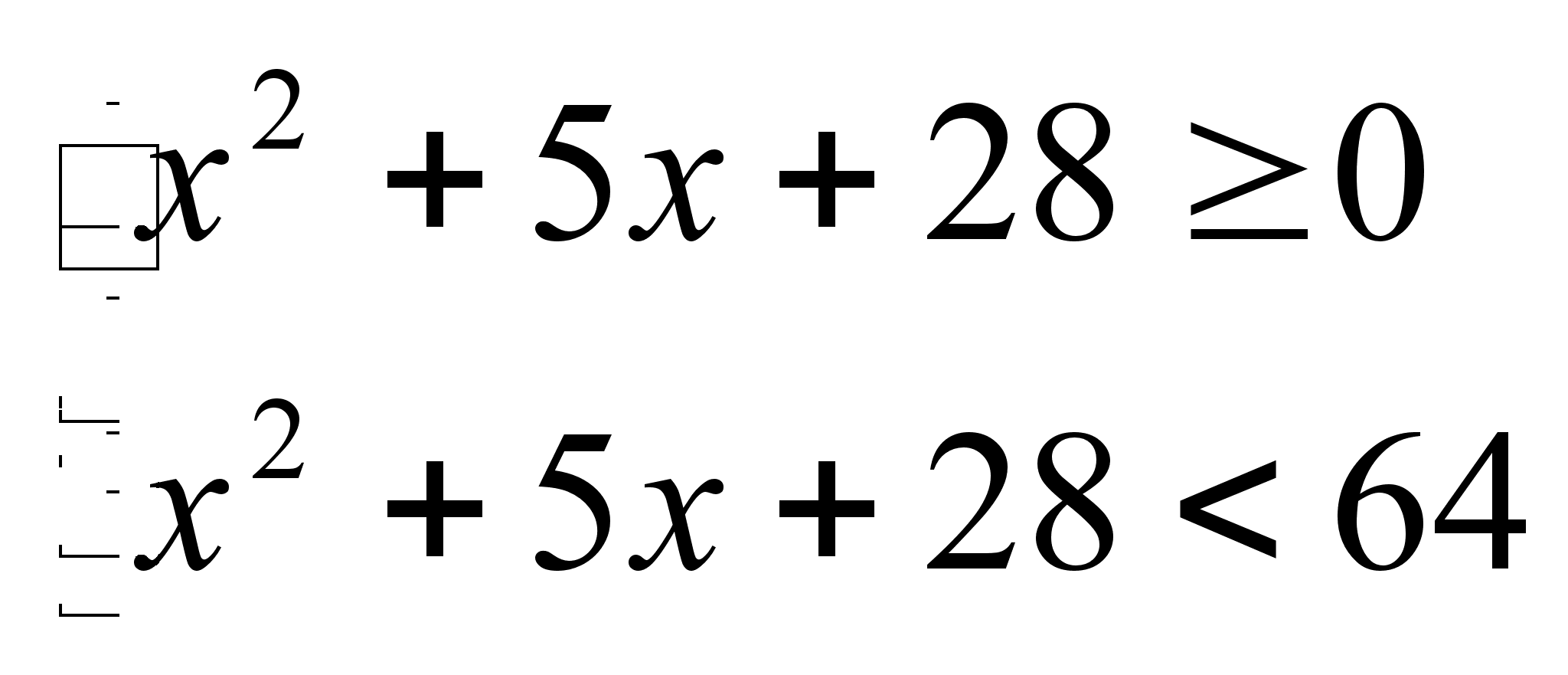
Так как неравенство х² + 5х + 38  0 выполняется при любых значениях х (D = 25 – 4  28  0 и а = 1  0), то последняя система равносильна неравенству:

х² + 5х + 38  0

или

(х + 9)(х – 4)  0

откуда методом интервалов находим решение неравенства (1)

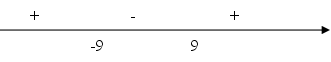
Ответ: х  ]-9; 4[

Неравенство (1) – неравенство вида

.

Здесь применима подстановка и неравенство заменяется равносильным ему неравенством:

у² – ky + d – c < 0, которое легко разрешимо.

Рассмотрим неравенство вида:

, где можно применить подстановку .

Пример 2. Решить неравенство:

Решение. Найдем ОДЗ неравенства: х  5. Положим , тогда у > x – 3, y  0. Выразим х через у: у² = 5 – х  х = 5 – у².

Получаем систему:

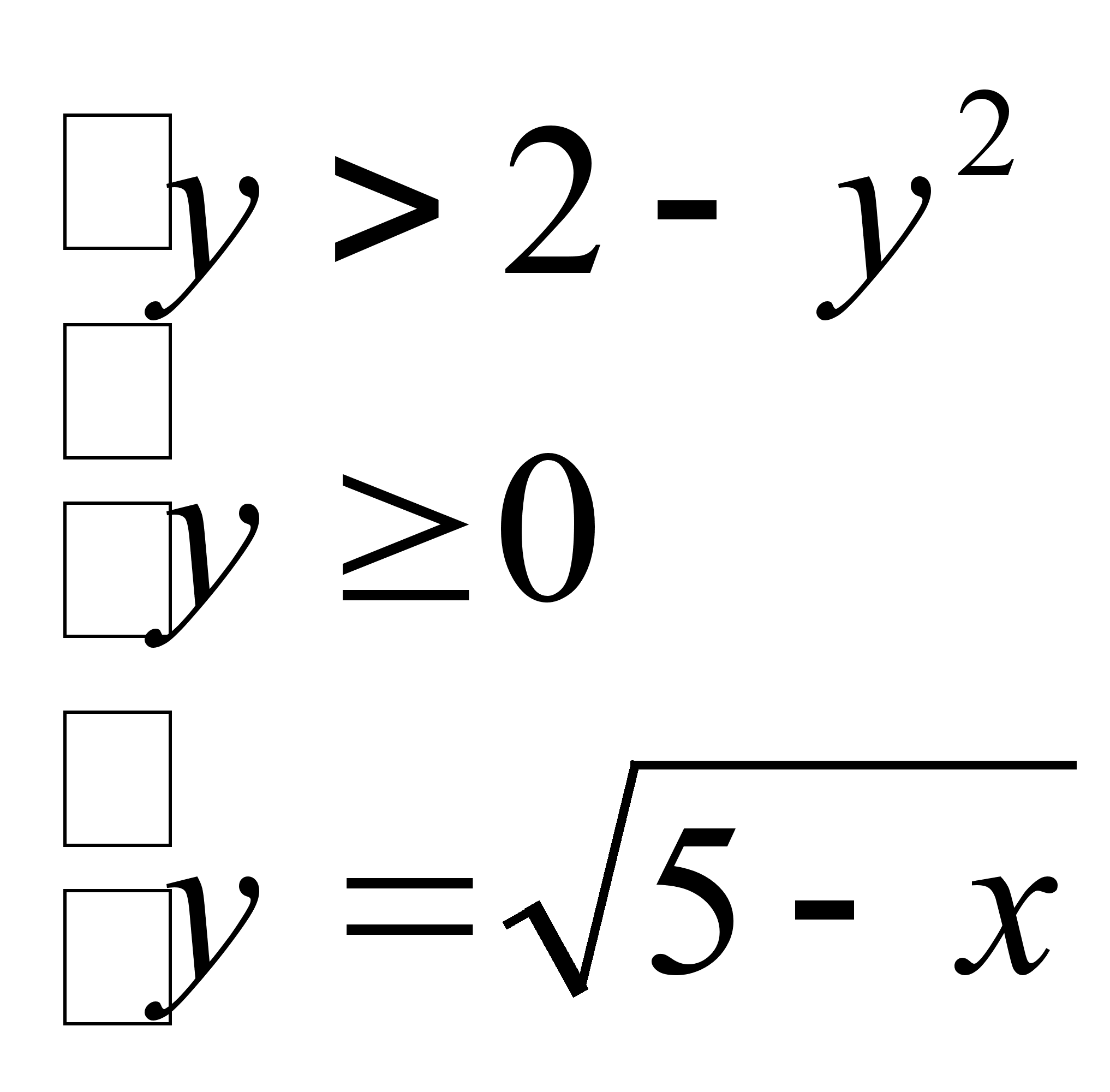
Откуда:

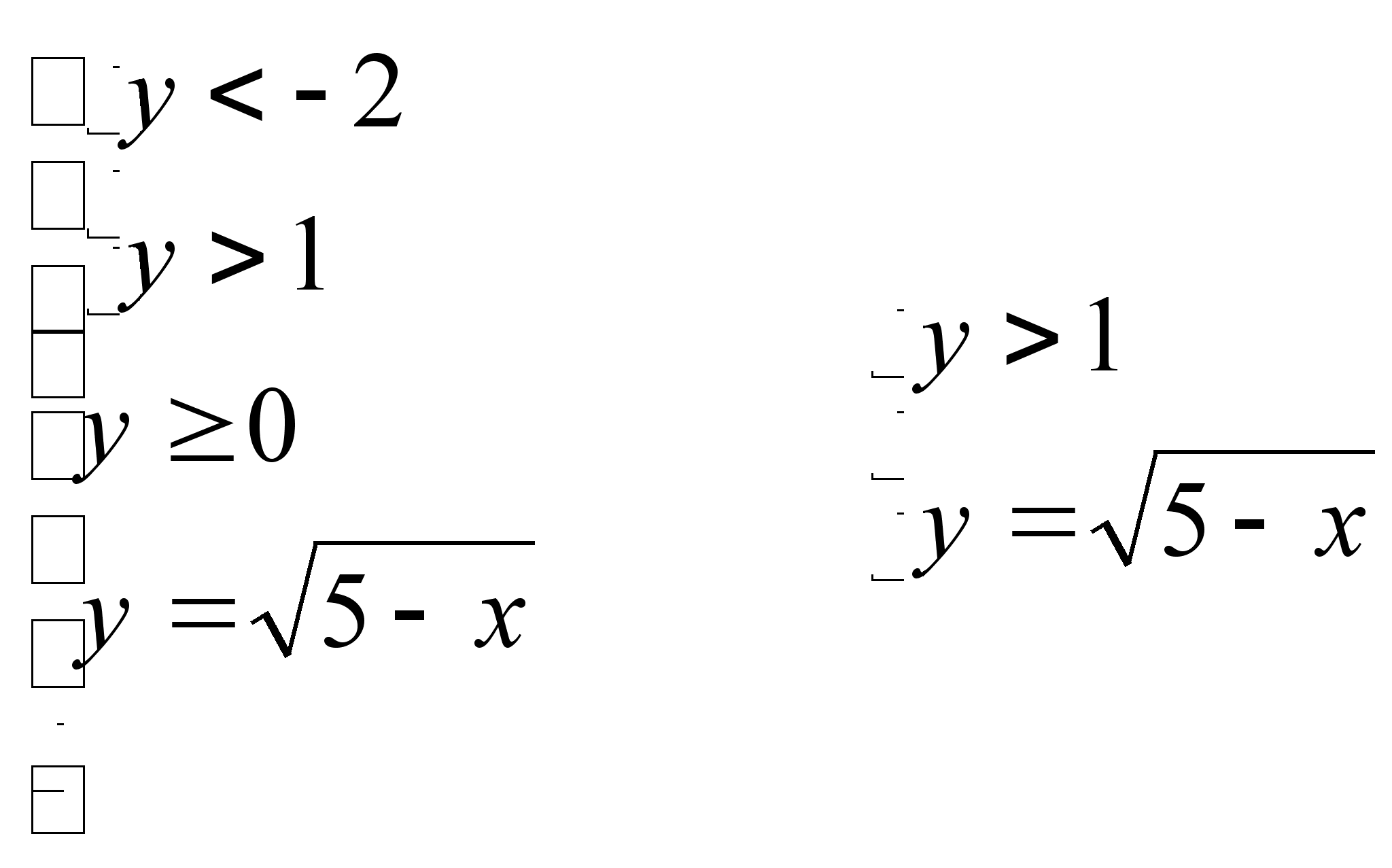
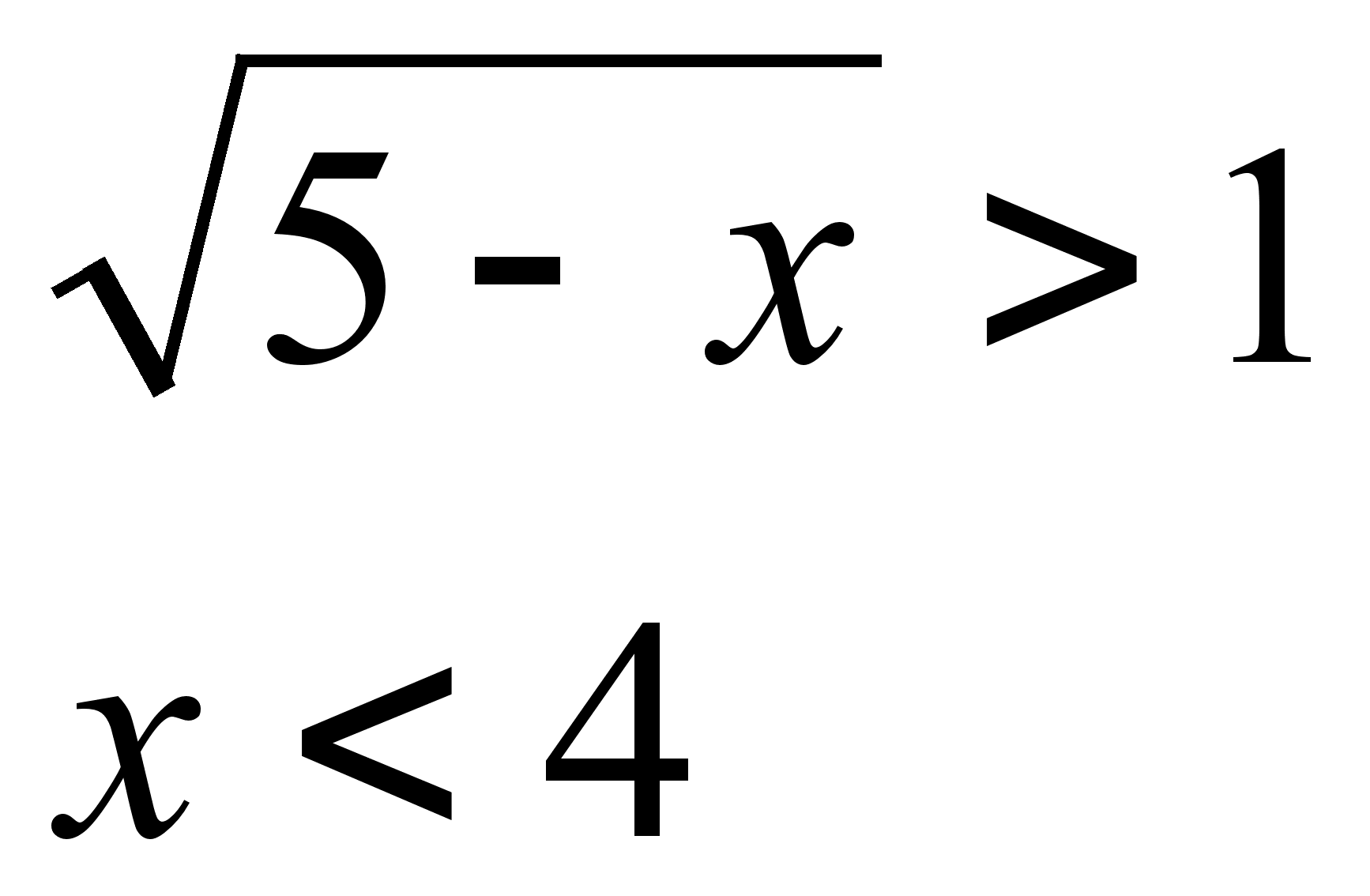
Значения x < 4 принадлежат ОДЗ.

Ответ: x < 4.

Пример 3. Решить неравенство

Решение. Найдем ОДЗ неравенства

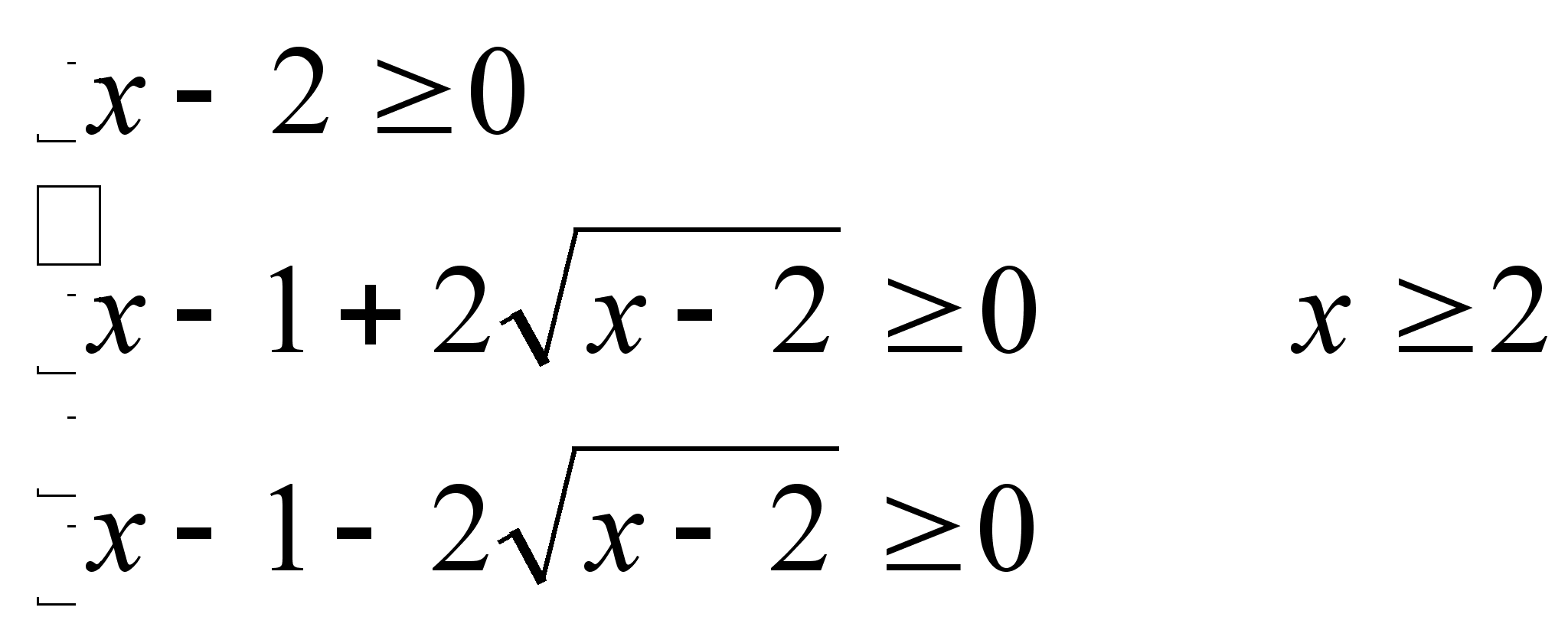
при х  2 второе и третье неравенства системы истинны. ОДЗ х  2.

Пусть , тогда исходное неравенство примет вид:

(1)

Так как под радикалами в левой части неравенства (1) стоят полные квадраты, то оно может быть представлено в следующем эквивалентном виде:

|t + 1| - |t – 1| > 1

Разобьем решение на три промежутка:

t  -1

-t – 1 + t – 1 > 1 

–1 < t  1

t + 1 + t – 1 > 1

2t > 1

t > Ѕ

t > 1

t + 1 – t + 1 > 1 2 > 1 – истинно

Подставляем

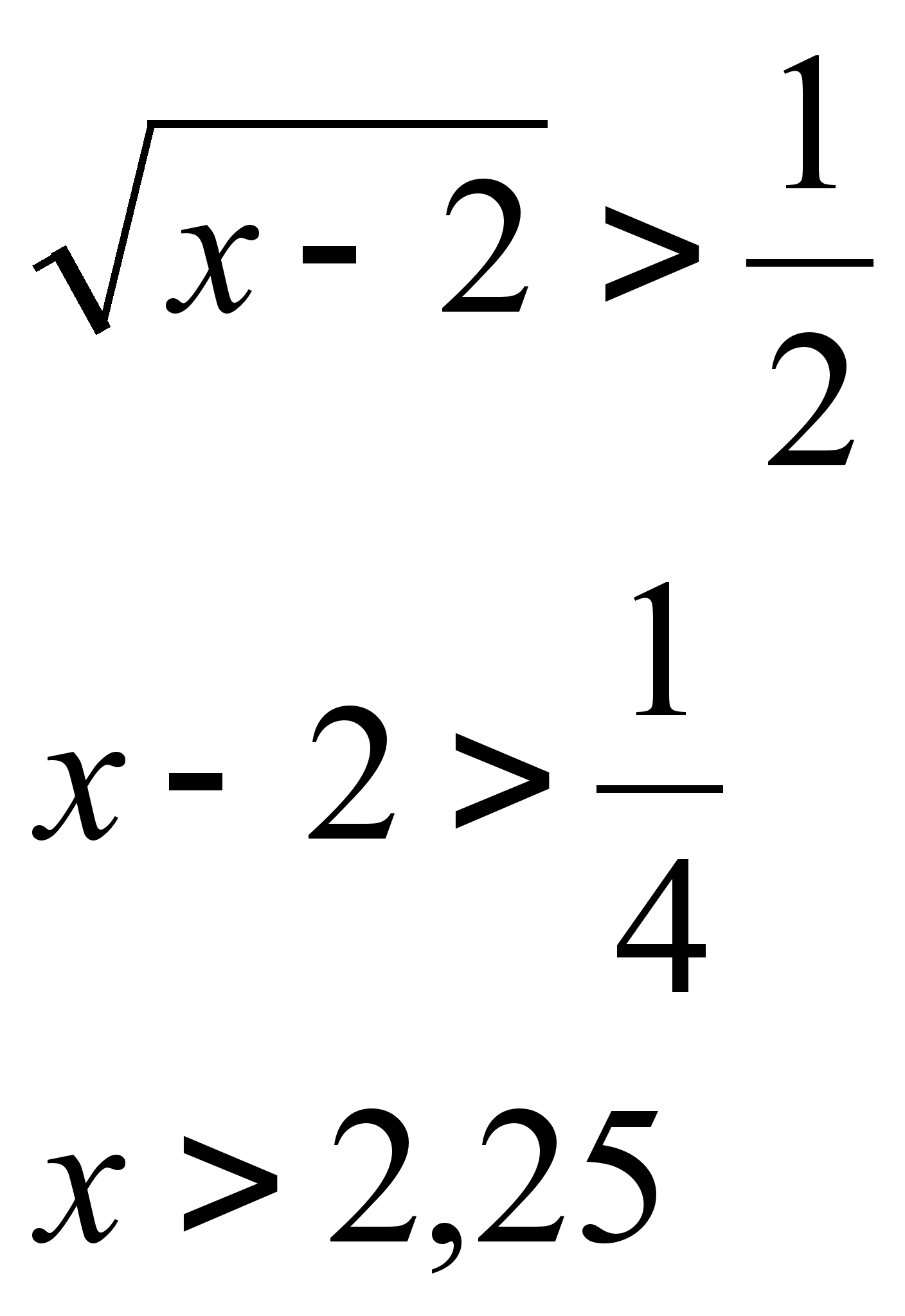
Эти значения принадлежат ОДЗ.

Ответ: x > 2,25.

Пример 4. Решить неравенство:

Решение. Положим , тогда и мы получаем неравенство:

у² – у – 2 >0,

откуда находим y < -1, y>2.

Теперь задача свелась к решению двух неравенств:

Первое неравенство не имеет корней во множестве действительных чисел, поскольку под знаком возведения в дробную степень может содержаться только неотрицательное число, а любая степень неотрицательного числа неотрицательна.

(1)

Пусть a < 0. В школьном курсе рациональная степень числа а не определяется, и это не случайно. Пусть (1) верно, тогда:

Противоречие.

Итак, получаем: левая положительная часть меньше отрицательной правой, что не имеет смысла.

Решим неравенство

Возведем обе части неравенства в пятую степень, получим x – 2 > 32, откуда x > 34.

Ответ: x > 34.

Похожие работы

Психолого-педагогическое обоснование внеклассной работы по математике

Скачать

113174

0

0

... говоря о том, что некоторые виды технических средств обладают исключительно большими возможностями наглядного показа материала обучения. Олимпиада одна из основных форм организации внеклассной работы по математике. Термин «олимпиада» проявился давно, хотелось бы вспомнить об истории отечественной математической олимпиады. Сначала о ней говорили в единственном числе, поскольку она организовывалась ...

Специальная педагогика

Скачать

899509

4

0

... и устойчивых требований, которые определяют характер и особенности организации коррекционно-образовательного процесса и управления познавательной деятельностью лиц с особыми образовательными потребностями. Специальная педагогика опирается на соответствующие обще- педагогические принципы организации образования и управления познавательной деятельностью, однако их реализация в системе специального ...

Исторические экскурсы в курсе алгебры 7 класса как средство развития познавательного интереса

Скачать

70672

3

3

... труде - все это формирует и развивает познавательный интерес и превращает его в важный стимул учебной деятельности учащихся [20,46]. Существуют различные средства развития познавательного интереса: решение занимательных, логических задач, игра, исторические экскурсы и другие. Наиболее подробно остановимся на исторических экскурсах. Знакомство с историей науки полезно для каждого человека, а для ...

Подготовка к Единому государственному экзамену по математике через элективные курсы

Скачать

45824

3

0

... учащихся к ЕГЭ, учителя математики СОШ №26 г.Якутска используют перечень вопросов содержания (кодификатор) школьного курса математики, усвоение которых проверяется при сдачи единого государственного экзамена 2007г. Элективный курс по подготовке к Единому Государственному Экзамену основан на повторении, систематизации и углублении знаний полученных ранее. Занятия проходят в форме свободного ...