Навигация
Группа подбирает и решает неравенства по теме «Решение иррациональных неравенств» способом введения новой переменной»
1 группа подбирает и решает неравенства по теме «Решение иррациональных неравенств» способом введения новой переменной».
2 группа решает неравенства
а) ![]()
б) ![]()
Тема: Решение иррациональных неравенств, способом введения новой переменной.
Цель: познакомить учащихся с методом решения иррациональных неравенств – введением новой переменной.
I. Разбор неравенств, приготовленных учащимися 1 группы.
II. Решить неравенства
1)
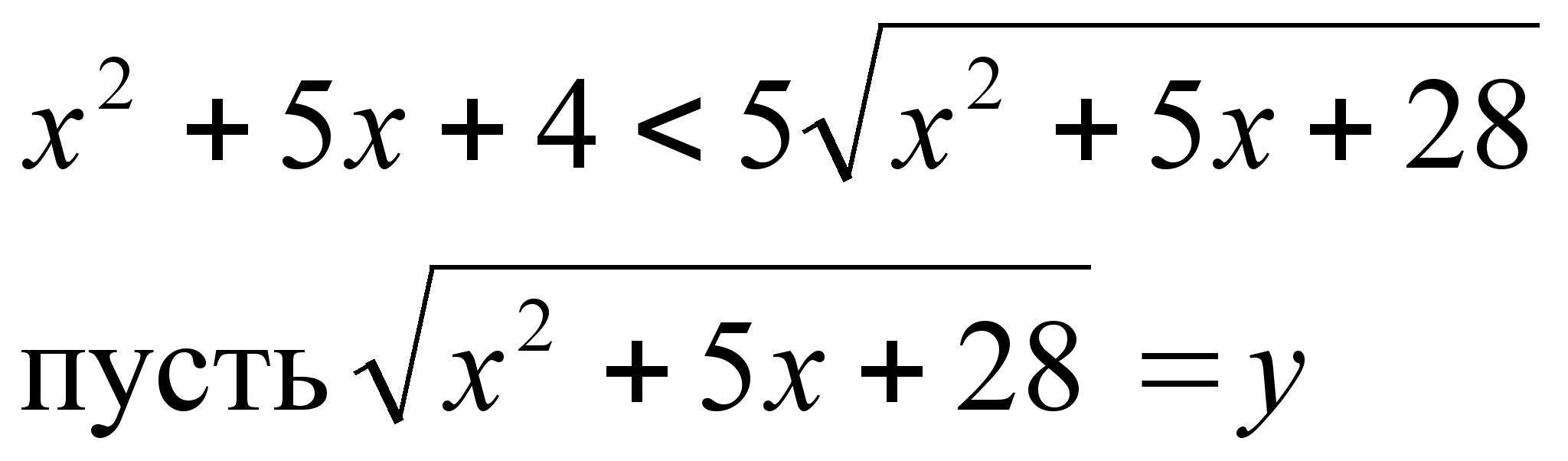
тогда х2 + 5х + 4 = у2 – 24
у2 – 5у – 24 < 0
у2 – 5у – 24 = 0
D = 25 + 96 = 121
у1 = -3 у2 = 8
(у – 8)(у + 3) < 0
-3 < y < 8
![]()
![]() -
истинно для
любого х
из ОДЗ: х2
+ 5х + 28
0 – истинно всегда
(D
< 0, a
> 0)
-
истинно для
любого х
из ОДЗ: х2
+ 5х + 28
0 – истинно всегда
(D
< 0, a
> 0)

Ответ: х ]–9; 4[
2)
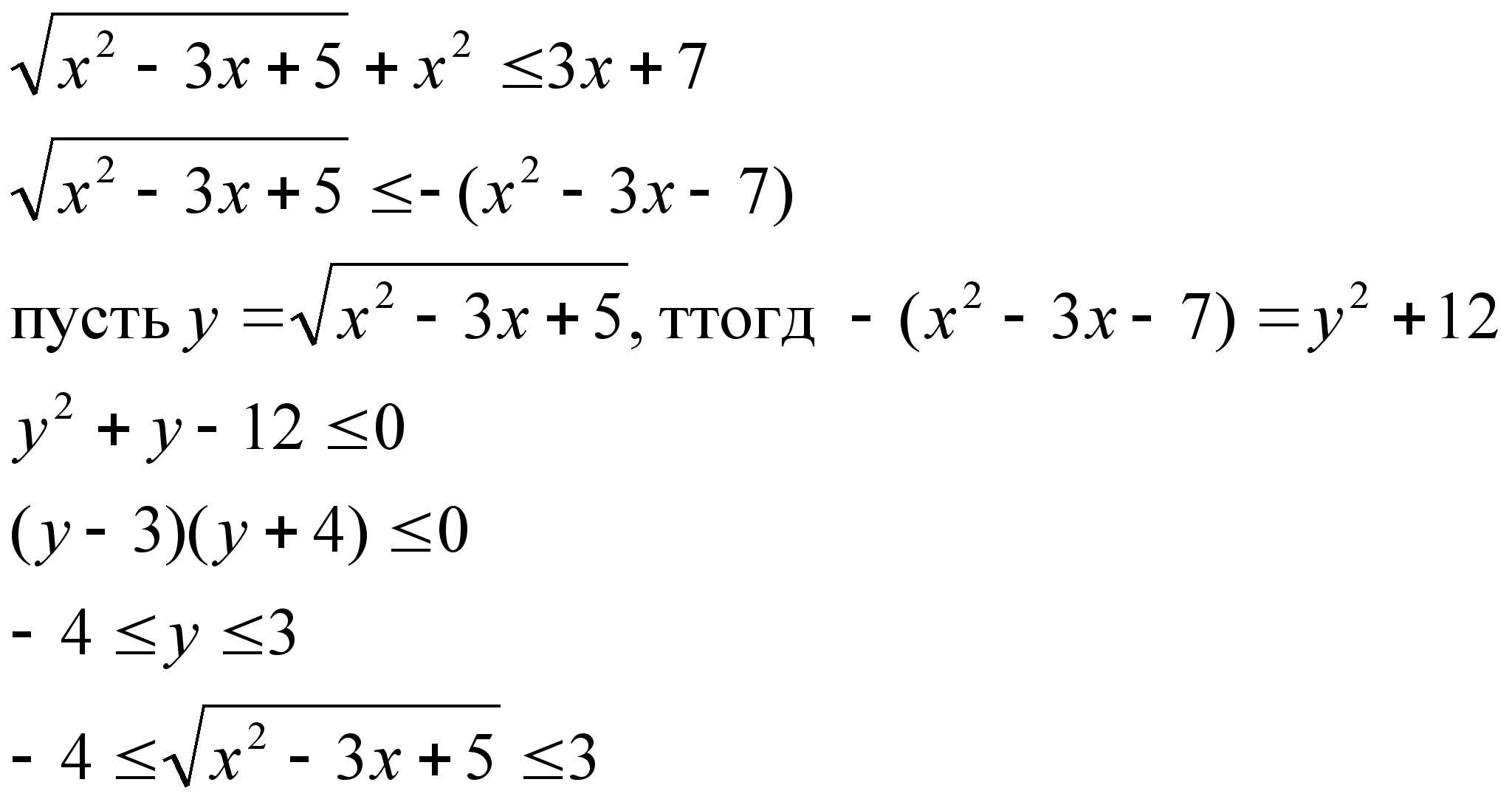
![]() - истинно
для любого
х из
ОДЗ х2
– 3х + 5
0 – истинно всегда
- истинно
для любого
х из
ОДЗ х2
– 3х + 5
0 – истинно всегда
D 0
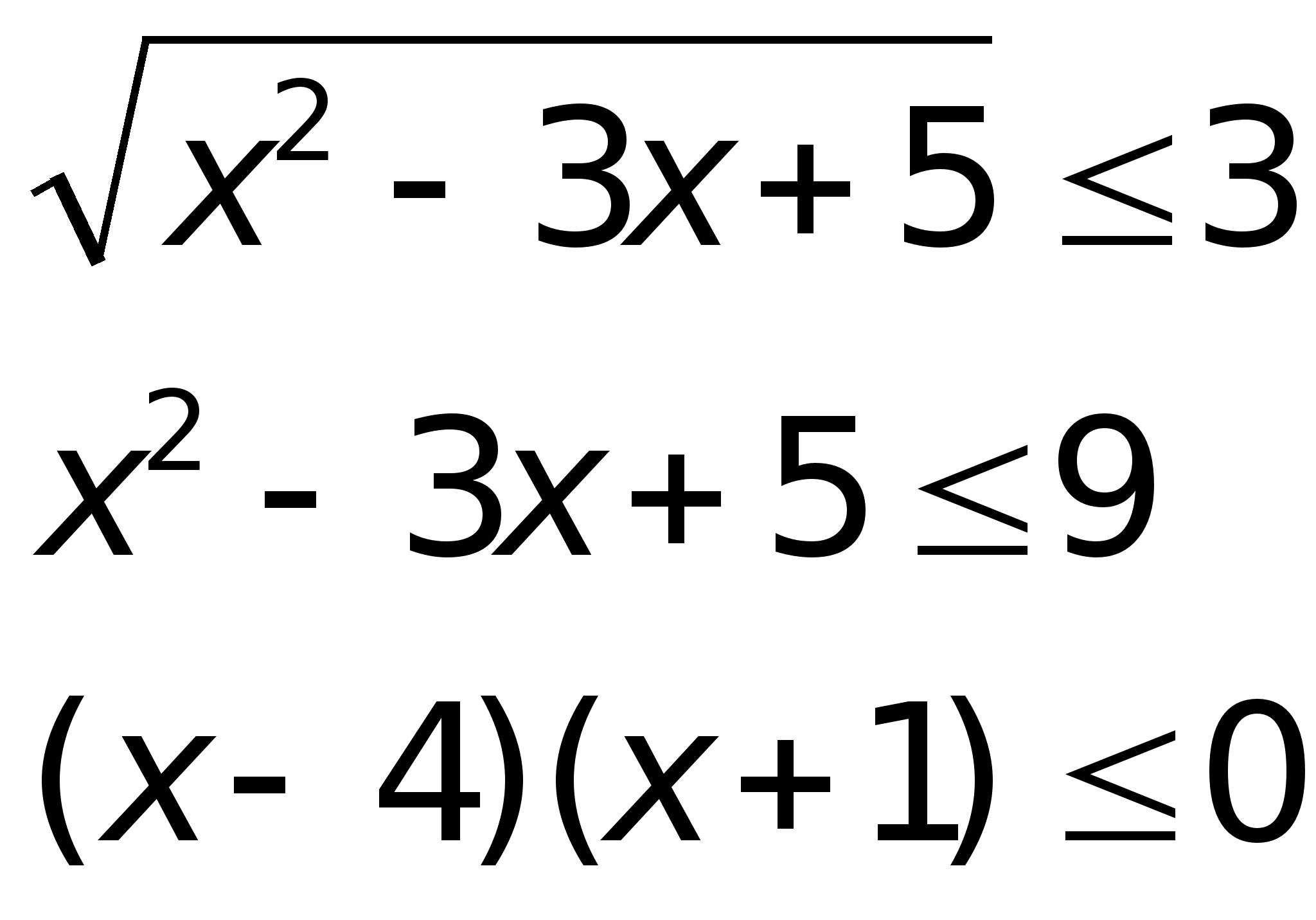
Ответ: х [-1; 4]
3)
![]()
ОДЗ: 5 – х 0 или х 5
пусть
![]() ,
тогда у
> x – 3, у
0
,
тогда у
> x – 3, у
0
выразим х через у: у2 = 5 – х х = 5 – у2
получаем систему:
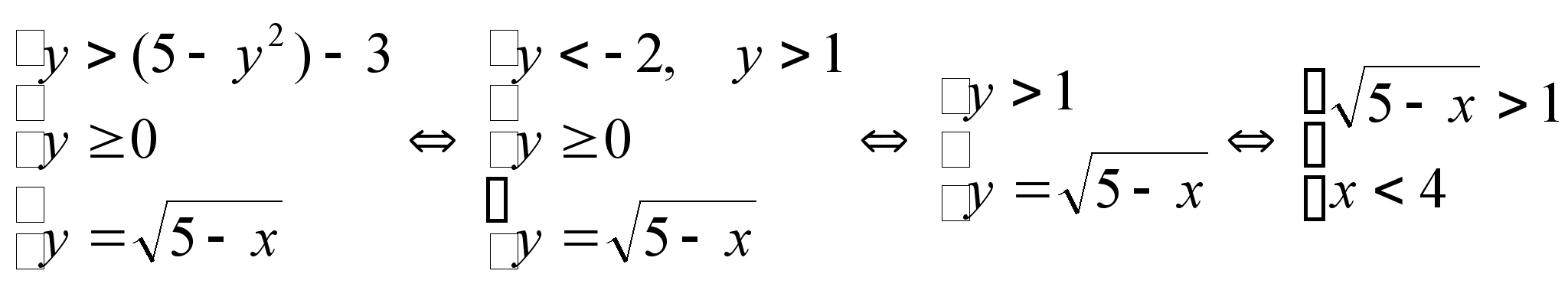
Значения х < 4 принадлежат ОДЗ
Ответ: х < 4
4) ![]()
ОДЗ: 2х
+ 10
0, х
-5 3x
– 5
0, x
![]()
пусть ![]() ,
тогда у
< 3x – 5,
y
0
,
тогда у
< 3x – 5,
y
0
выразим х через у : у2 = 2х + 10 х = Ѕу2 – 5
получаем систему:
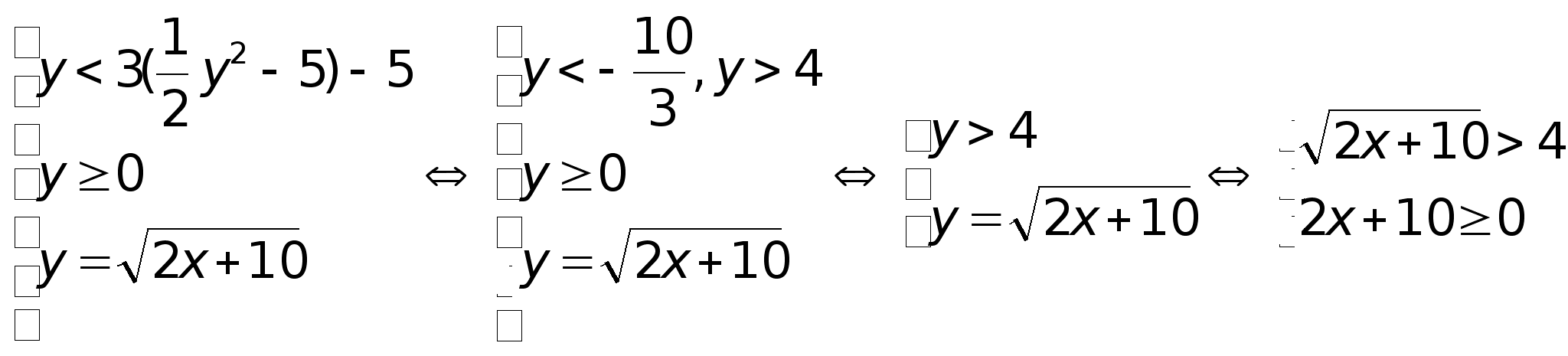 x
> 3
x
> 3
Значения х > 3 принадлежат ОДЗ
Ответ: х > 3
5)![]()
Найдем ОДЗ неравенства:
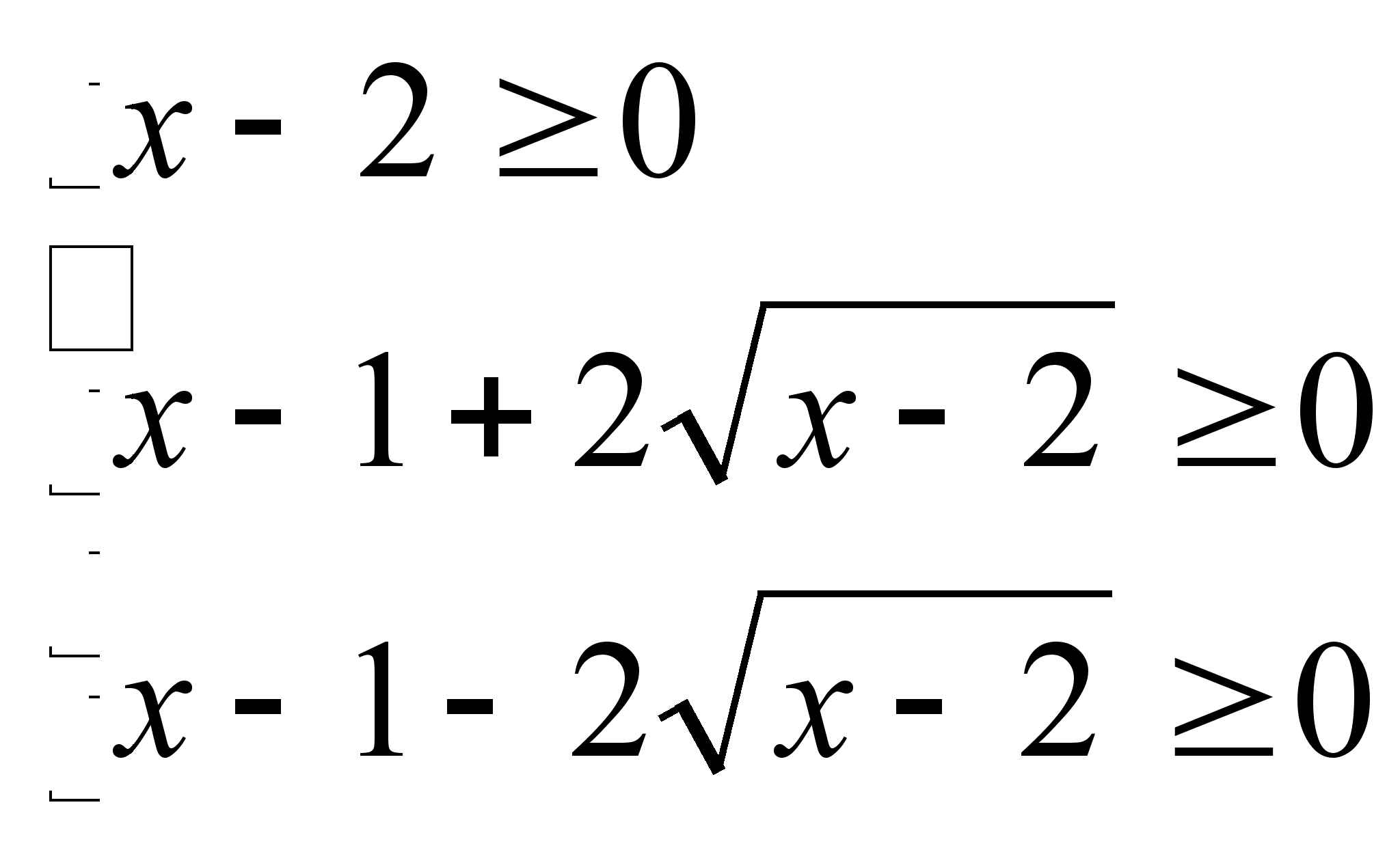
х 2
при х 2 второе и третье неравенства системы истинны
ОДЗ: х 2
пусть ![]()
![]()
|t + 1| - |t – 1| > 1
a) t -1
-t – 1 + t – 1 > 1
-2 > 1 – ложно
б) –1 < t 1
t
+ 1 + t
–1 >1
![]()
учитывая,
что –1
< t
1, получаем
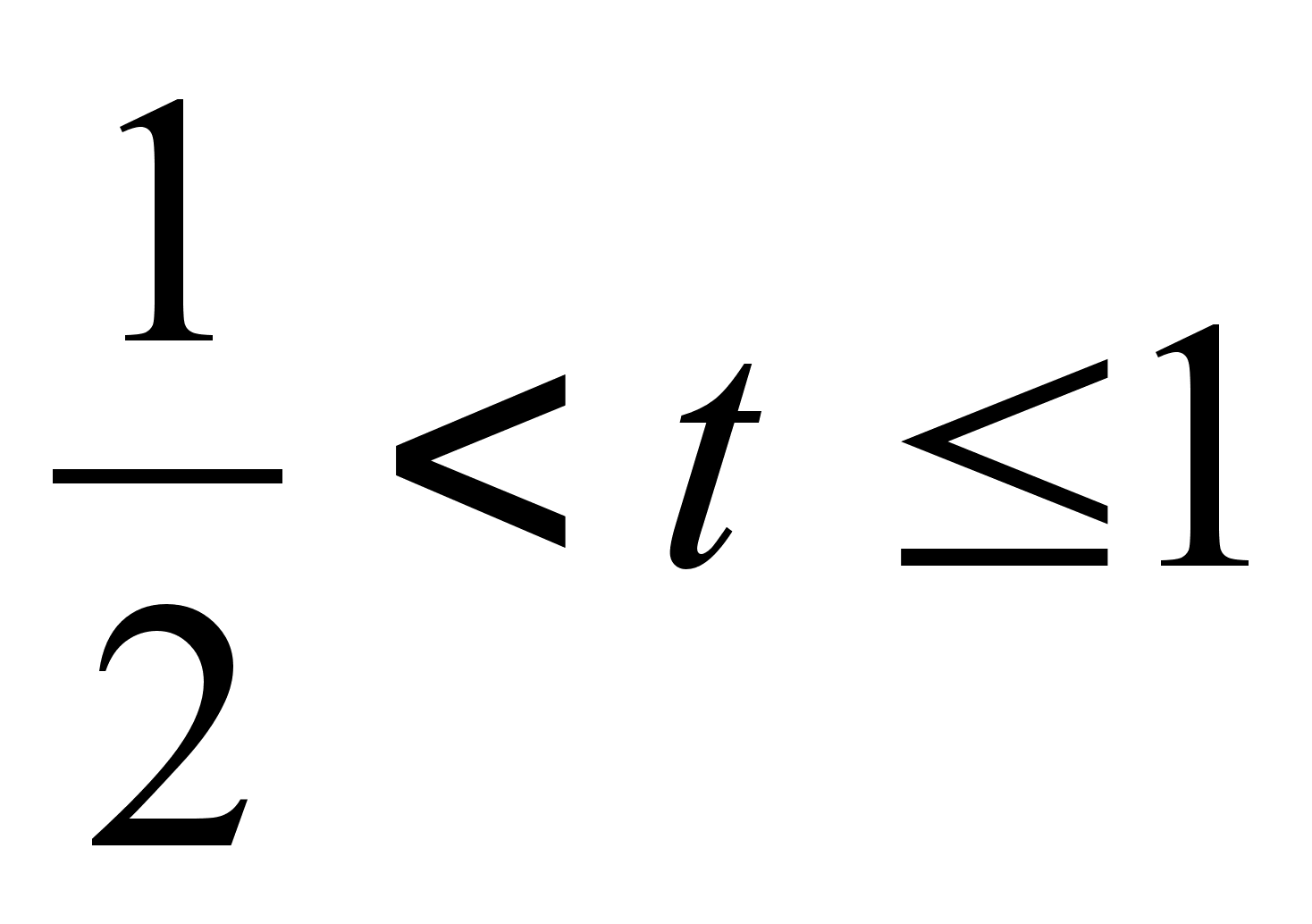
в) t > 1
t + 1 – t + 1 > 1 2 > 1 – истинно
решением
неравенства
на всех трех
промежутках
будет ![]()
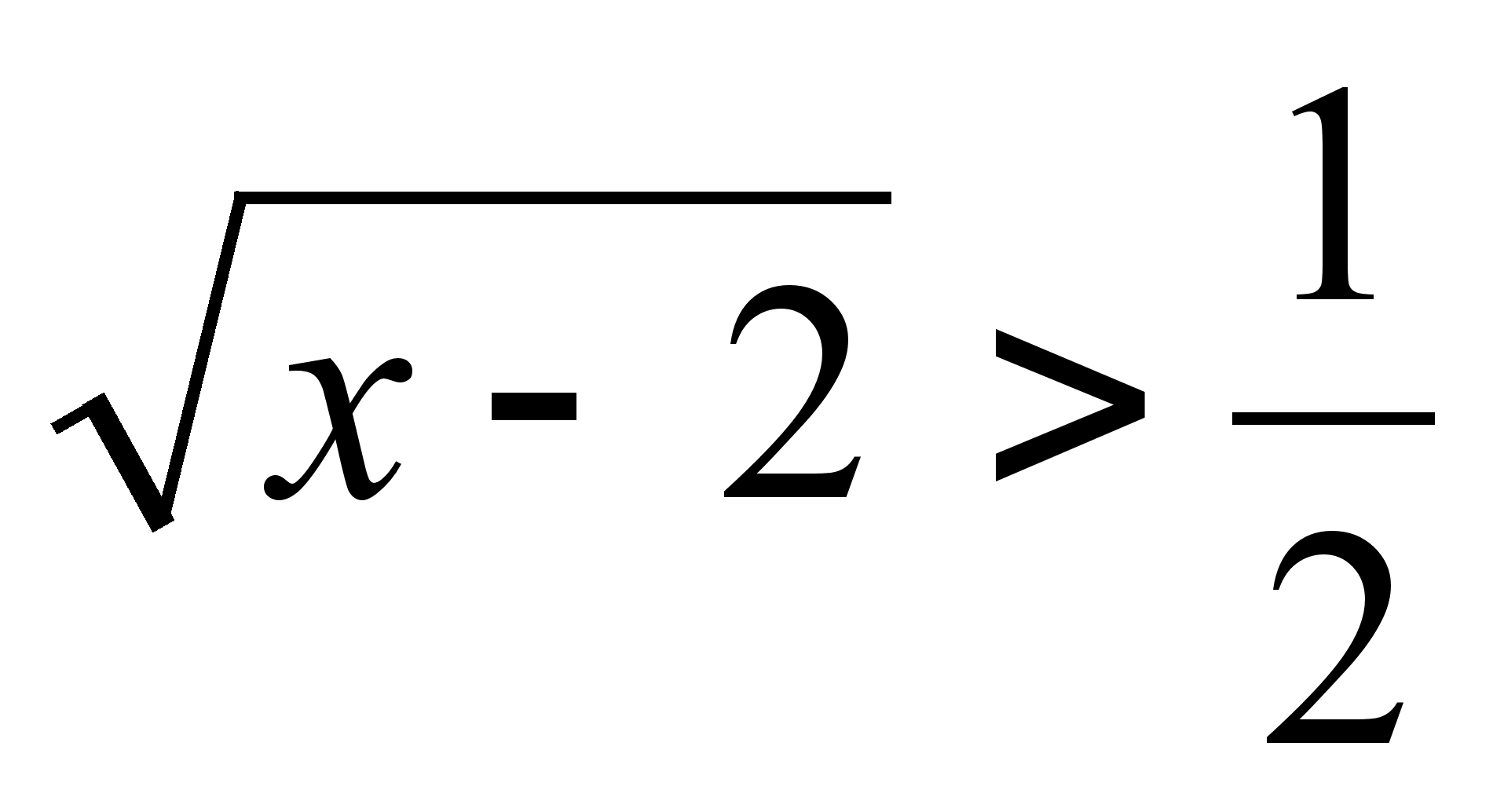
x > 2,25 – принадлежит ОДЗ
Ответ: x > 2,25
6) ![]()
ОДЗ неравенства:
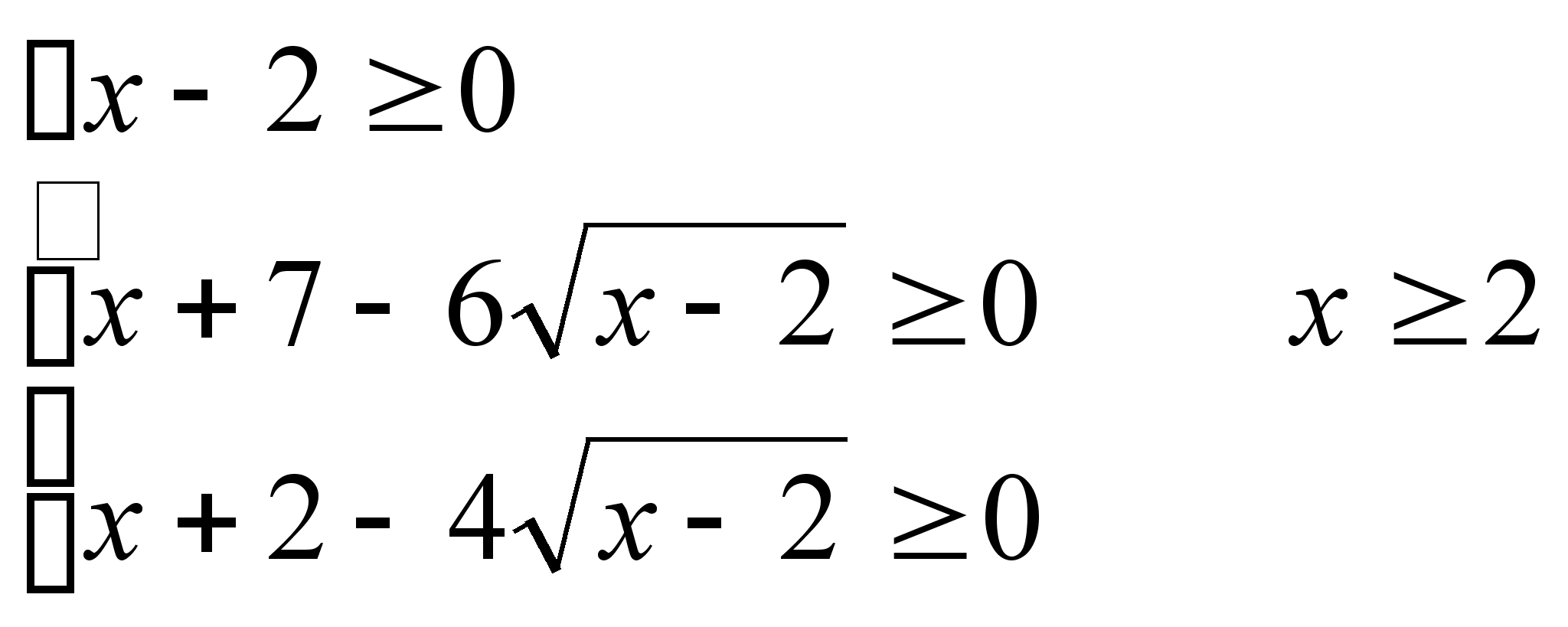
пусть ![]() ,
тогда
,
тогда
![]()
|t +-3| + |t – 2| > 1
a) t 2
- t + 3 – t + 2 > 1 t 1 – ложно
в) t > 3
t – 3 + t – 2 > 1 t >3
получаем:
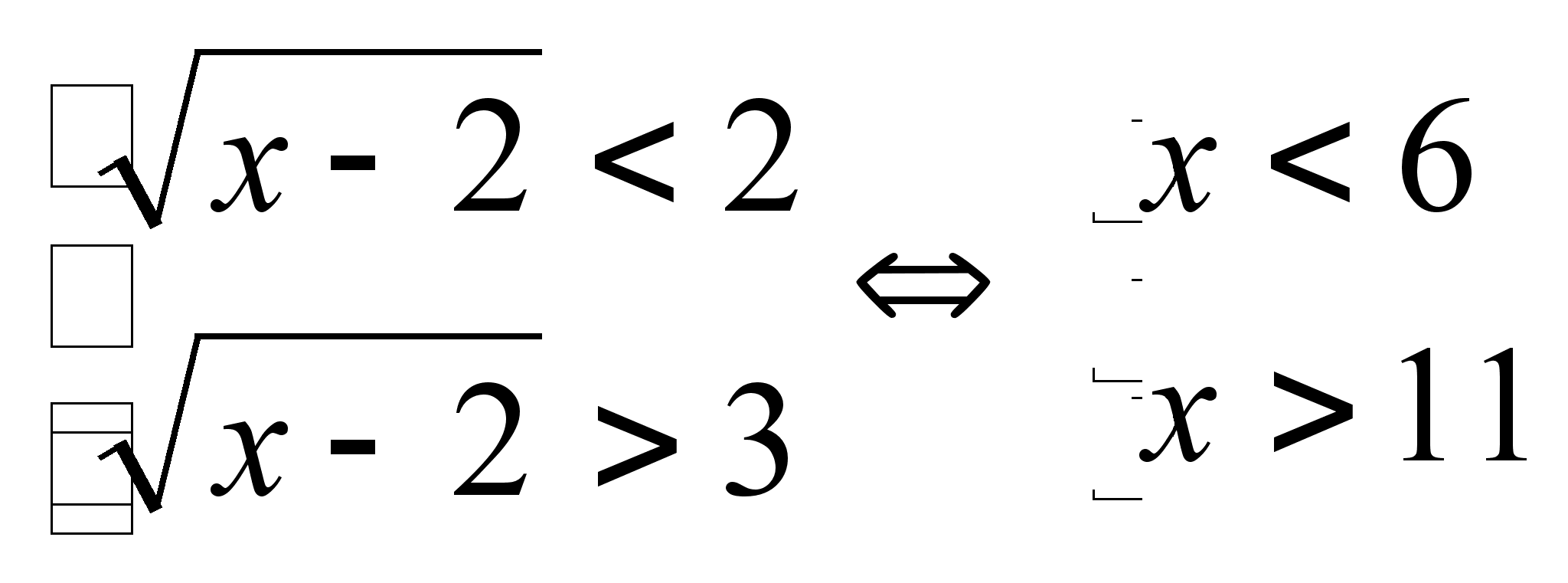
учитывая ОДЗ получаем: 2 x < 6, x > 11
Ответ: 2 x < 6, x > 11
III. Д/з
1 группа разбирает способы решения иррациональных неравенств домножением обеих частей на некоторое число или выражение, разложением подкоренного выражения на множители, выделением полного квадрата в подкоренных выражениях.
2 группа решает неравенства:
а) ![]()
б) ![]()
Занятие № 8
Тема: Решение иррациональных неравенств, способами домножения обеих частей на некоторое число, либо выражение, выделения полного квадрата в подкоренных выражениях, либо разложения подкоренного выражения на множители.
Цель: дать учащимся представление о способах решения иррациональных неравенств.
I. Разбор Д/з 2 группы (устно)
II. Разбор задач, приготовленных 1 группой.
III. решить неравенства
![]()
ОДЗ: х 1
домножим на ![]()
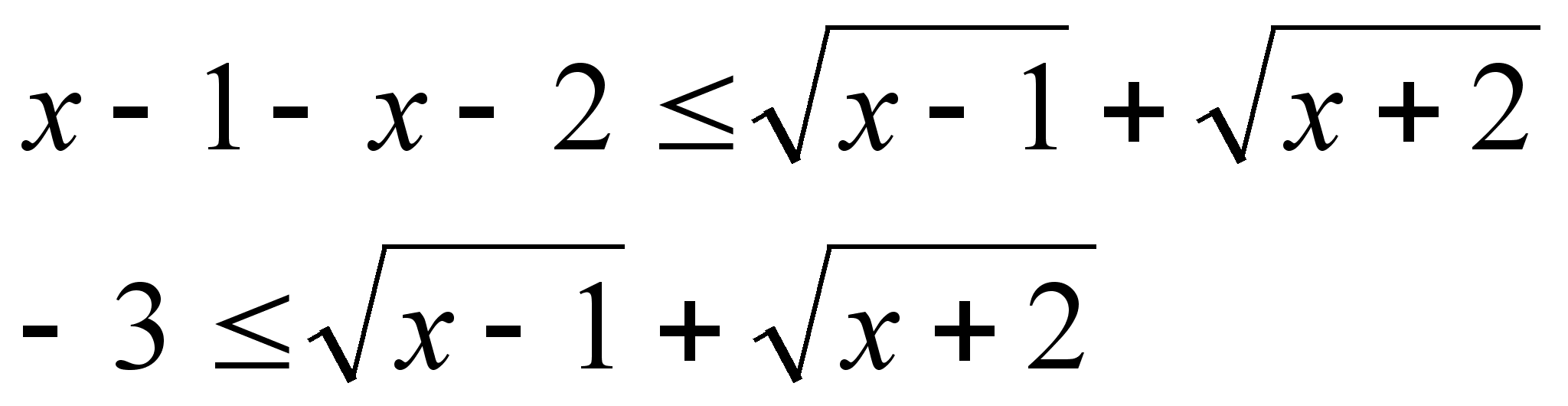
последнее неравенство всегда истинно на ОДЗ
Ответ: х 1
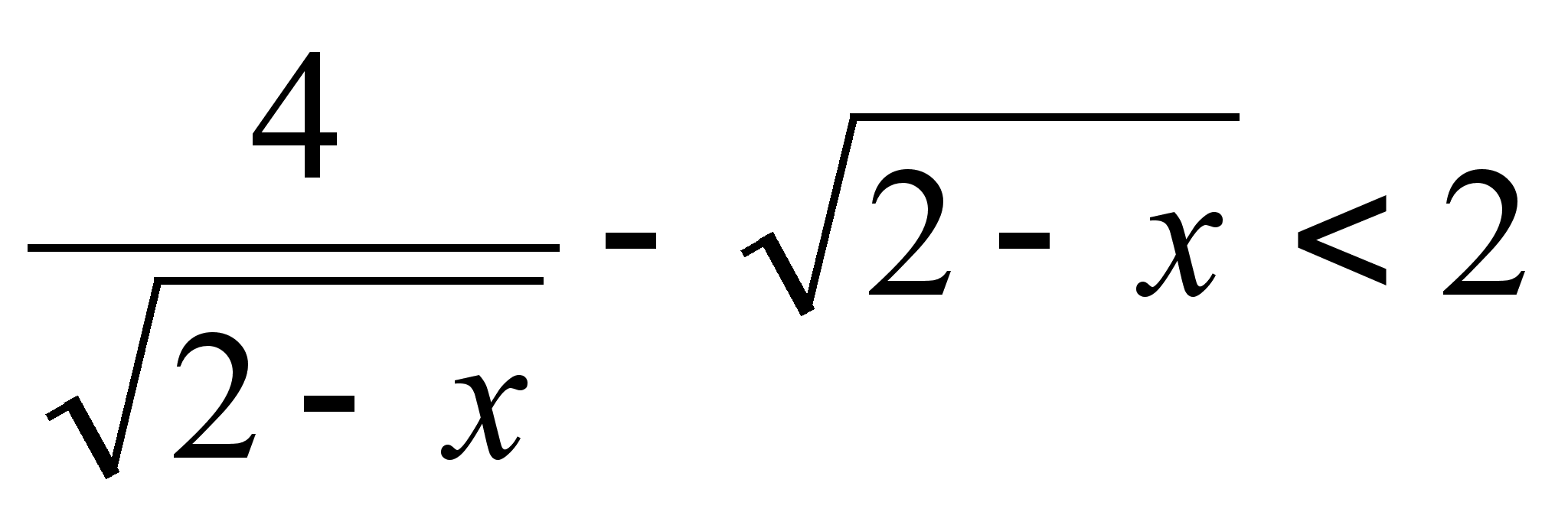
ОДЗ: х < 2
домножим на ![]()
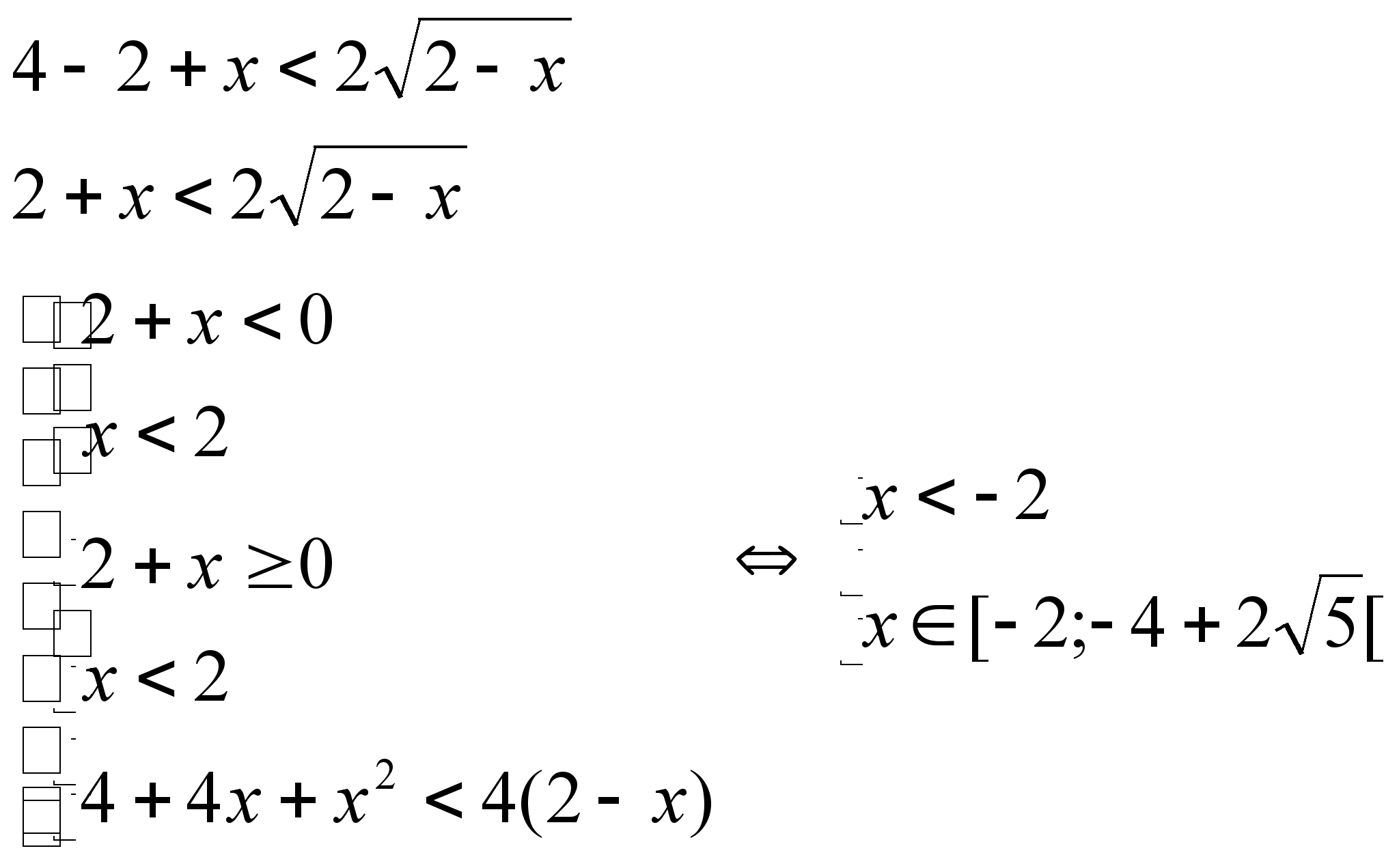
Ответ: ![]()
3)
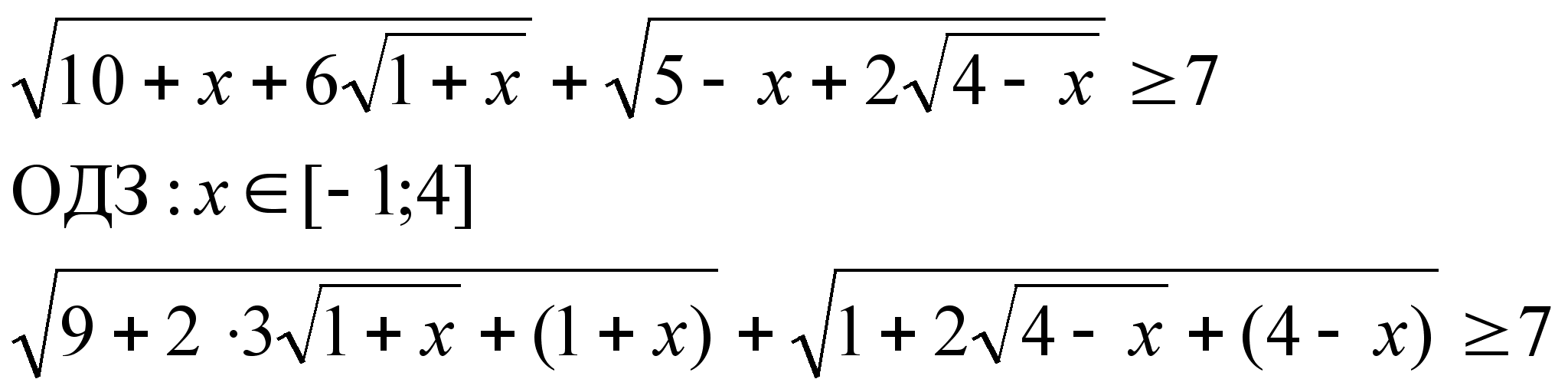
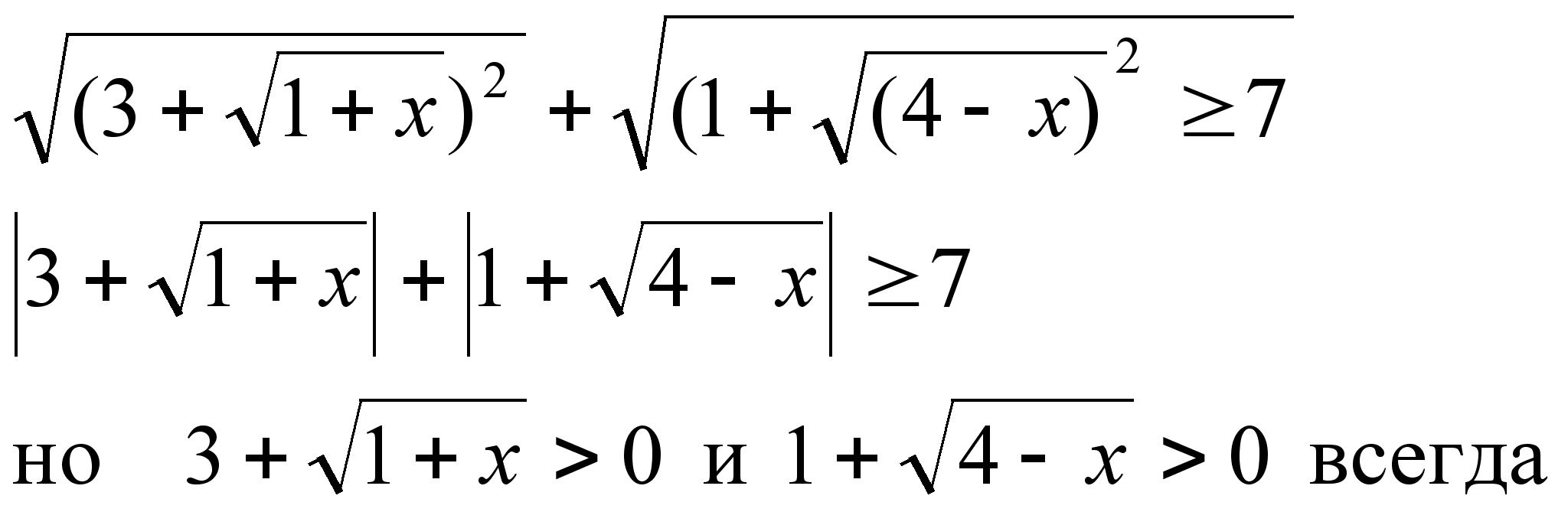
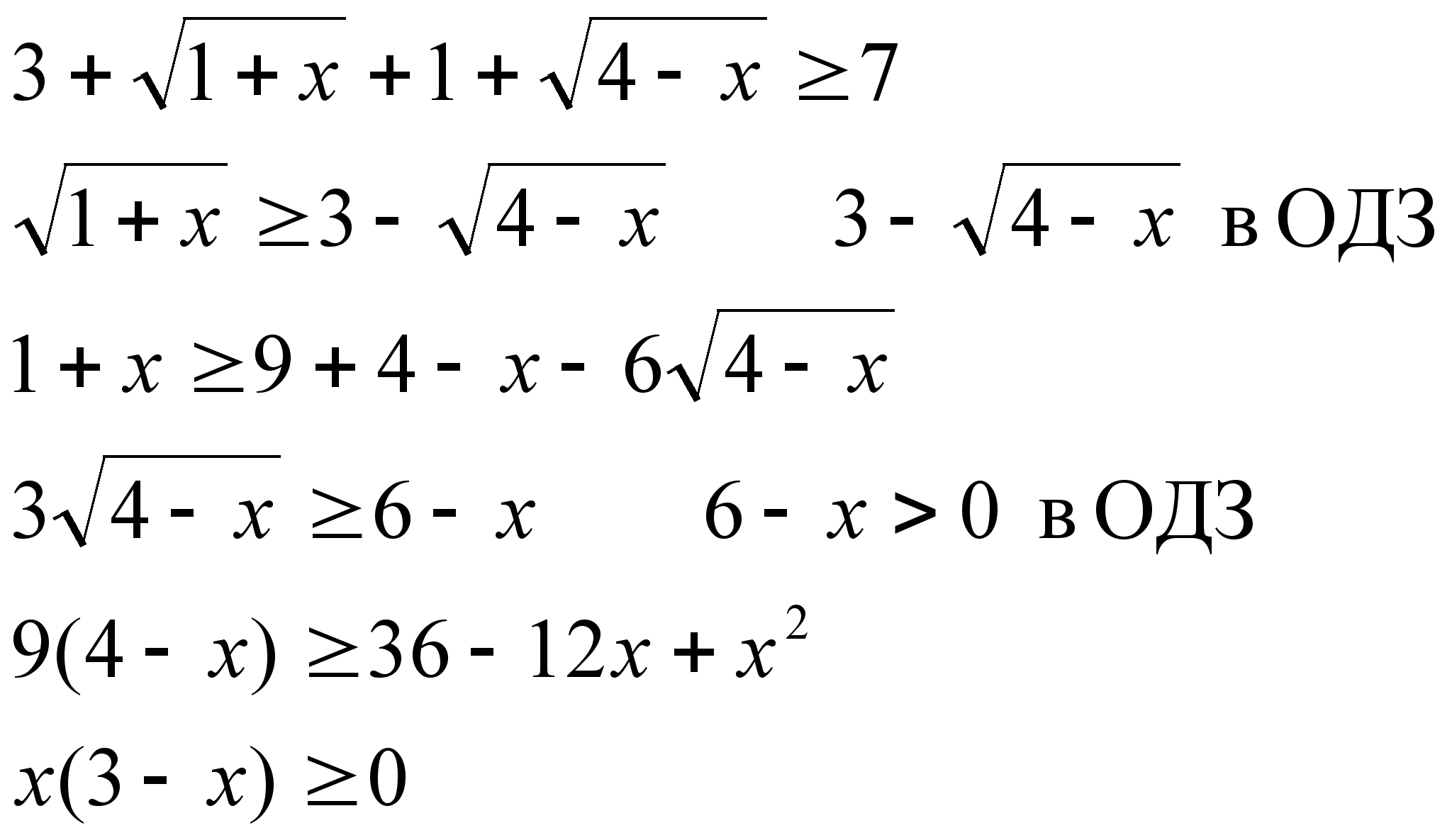
Ответ: х[0;3]
4) ![]()
ОДЗ: х 1, х 5, х = 2
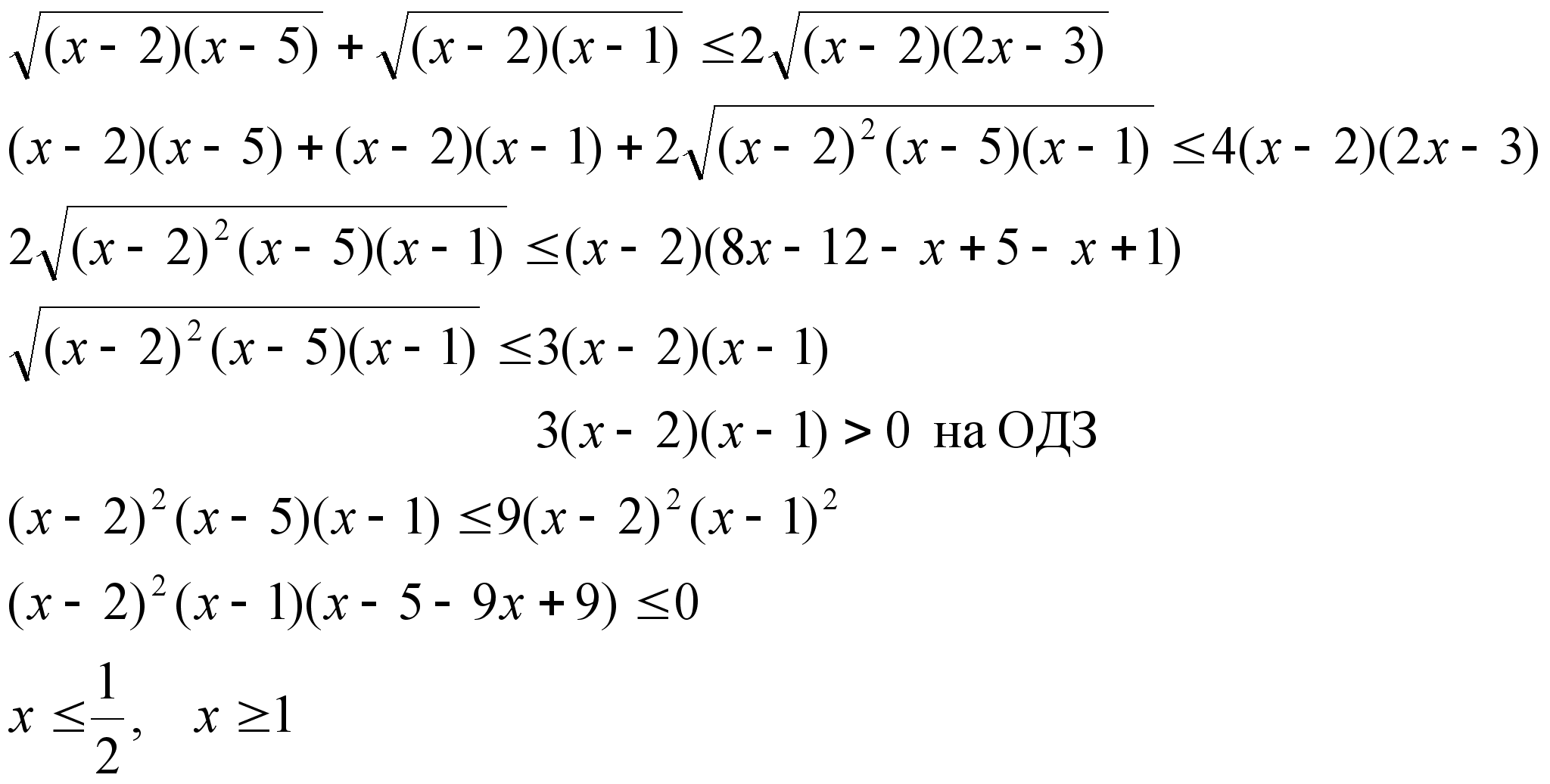
учитывая ОДЗ получаем
Ответ: ![]()
Итоговая контрольная работа
Вариант I.
Решить неравенства
![]()
![]()
![]()
![]()
![]()
Вариант II.
Решить неравенства
![]()
![]()
![]()
![]()
![]()
Филиппова Ольга Владимировна.
Дипломная работа «Организация познавательной деятельности учащихся на факультативных занятиях по теме «Иррациональные неравенства»
Руководитель: Кузьмичев Анатолий Иванович.
З А Щ И Т А (устно)
Дипломная работа состоит из введения, трех глав, заключения, списка литературы и приложения с разработкой факультатива по теме.
В дипломной работе мне хотелось собрать и проанализировать знания, полученные за пять лет обучения, и применить их к конкретной задаче. А именно, я попыталась на примере изучения очень трудной и, прямо сказать, непопулярной среди школьников темы «Иррациональные неравенства» подтвердить положение о том, что интерес, а с ним и знания, умения, навыки приходят вместе с упорным трудом, причем, этот труд должен носить в большой мере самостоятельный характер и в части подготовки к занятиям, и даже части проведения и поиска нужных форм их организации.
Важным подспорьем в развитии познавательного интереса учащихся являются, как оказалось, исторические сведения по теме. Их поиск значительно активизировал работу с литературой, в которой помимо всего учащиеся искали еще и сведения по методике проведения занятий, изучения темы, задач, предлагавшихся на вступительных экзаменах в различные ВУЗы.
При проведении факультативных занятий ученики были разбиты на 2 группы: экспериментальную и контрольную, примерно равные по силам. У всех учащихся была одна цель – подготовиться к вступительным экзаменам в ВУЗ. Это определило их первоначальный интерес. Разбиение на 2 группы проводилось по желанию самих ребят. Они посещали одни и те же занятия, изучали на уроках один и тот же материал. Но ребята 1-ой экспериментальной группы имели гораздо больше возможностей и причин для самостоятельной работы по теме: они в качестве домашнего задания должны были самостоятельно изучить новую тему, начиная с поиска материала (под руководством учителя), далее написать доклады, найти и прорешать задачи, а затем рассказать все это остальным участникам факультатива.
Учитель предлагал темы, литературу, определял докладчиков, акцентировал в нужных местах внимание и на уроках давал задачи по теме, которые, по его мнению, нужно было прорешать, а докладчики таковых не предложили.
Заключительная работа по теме показала, что учащиеся из 1-ой группы получили результаты, пусть и ненамного, но лучше учащихся контрольной группы.
Но, кроме того, они получили бесценный опыт самостоятельной работы, который, как мне кажется, еще даст свои положительные результаты в будущем.
По материалам проведенного факультатива и был написан диплом.
В первой главе разбираются основные формы организации познавательной деятельности, проводится их сравнительный анализ и выясняются оптимальные сочетания и взаимодействия этих форм (в зависимости от специфики материала и от того, как он усвоен учащимися, выбирались сочетания фронтальной, групповой и индивидуальной форм).
Во второй главе рассматриваются вопросы методики организации факультативных занятий, необходимость и обоснованность их проведения. Далее излагаются результаты опытно-экспериментальной работы.
Глава три – основная часть работы. В ней содержится необходимый теоретический и практический материал для факультатива. К сожалению, сюда не вошли все задачи, которые предлагали учащиеся, найденные ими к занятиям, из-за их однотипности с опубликованными.
Учащимися, с помощью учителя, были выделены 9 частных случаев и способов решения иррациональных неравенств и к каждому из них учащиеся придумывали неравенства для последующего решения их всем классом.
Учителем была поставлена задача выяснить, какие трудности характерны для каждого из способов решения.
Большое внимание уделялось оформлению решения задачи, в частности, записи ответа, за что в ВУЗах на приемных экзаменах часто снижают бал.
Эта часть диплома может служить основой для проведения соответствующего факультатива для любого учителя. Данная глава заканчивается подборкой задач по теме и доказательством классических неравенств.
В приложении приводится разработка факультатива из 8 занятий по теме «Иррациональные неравенства» и итоговая контрольная работ
Похожие работы
... говоря о том, что некоторые виды технических средств обладают исключительно большими возможностями наглядного показа материала обучения. Олимпиада одна из основных форм организации внеклассной работы по математике. Термин «олимпиада» проявился давно, хотелось бы вспомнить об истории отечественной математической олимпиады. Сначала о ней говорили в единственном числе, поскольку она организовывалась ...
... и устойчивых требований, которые определяют характер и особенности организации коррекционно-образовательного процесса и управления познавательной деятельностью лиц с особыми образовательными потребностями. Специальная педагогика опирается на соответствующие обще- педагогические принципы организации образования и управления познавательной деятельностью, однако их реализация в системе специального ...
... труде - все это формирует и развивает познавательный интерес и превращает его в важный стимул учебной деятельности учащихся [20,46]. Существуют различные средства развития познавательного интереса: решение занимательных, логических задач, игра, исторические экскурсы и другие. Наиболее подробно остановимся на исторических экскурсах. Знакомство с историей науки полезно для каждого человека, а для ...
... учащихся к ЕГЭ, учителя математики СОШ №26 г.Якутска используют перечень вопросов содержания (кодификатор) школьного курса математики, усвоение которых проверяется при сдачи единого государственного экзамена 2007г. Элективный курс по подготовке к Единому Государственному Экзамену основан на повторении, систематизации и углублении знаний полученных ранее. Занятия проходят в форме свободного ...
0 комментариев