Решение иррациональных неравенств путем проб, выводов

11. Решение иррациональных неравенств путем проб, выводов.

Пример 1. Решить неравенство:

(1)

Решение. Область определения неравенства (1): 2  х  3.

Прежде, чем возводить в квадрат обе части неравенства (1), необходимо убедиться в том, что обе его части неотрицательны.

Однако, оказывается, что это не так.

Действительно, так как 2  х  3, то 1  х – 1  2 и 3  6 – х  4. А это значит, что или . Но . Таким образом, при всех значениях х из отрезка 2  х  3 неравенство (1) выполняется. Итак, 2  х  3 - решение неравенства.

Пример 2. Решим неравенство:

Решение. Найдем ОДЗ неравенства:

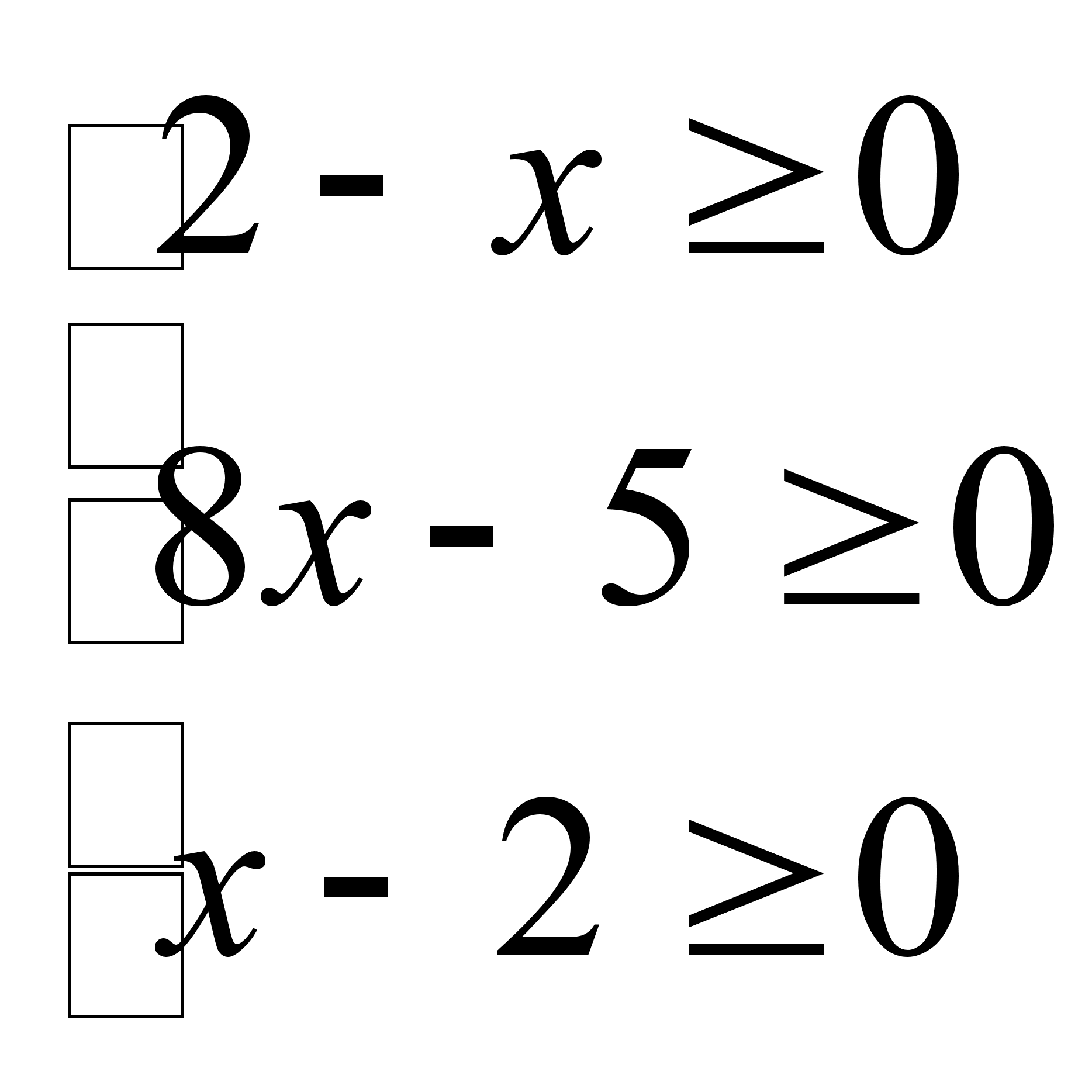
откуда получаем, что ОДЗ неравенства х = 2 – единственная точка. Подстановкой легко проверить, что х = 2 является решением исходного неравенства.

Ответ: х = 2.

12. Решение более сложных примеров.

Пример 1. Решить неравенство

Решение. Используем метод интервалов. Решим соответствующее уравнение.

Решением уравнения являются значения переменной х = 0 и при любом действительном значении параметра а.

Корни соответствующего уравнения разбивают числовую ось на промежутки знакопостоянтства, в каждом из которых неравенство или тождественно истинное, или тождественно ложное.

а) если a > 0, то и числовая ось разбивается на следующие промежутки знакопостоянства: x

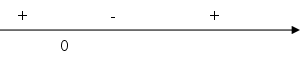
Рассмотрим промежуток . Возьмем значение х = а из этого промежутка и подставим в данное неравенство. Получим: - истинное числовое неравенство. Следовательно, промежуток принадлежит решению. Любое значение переменной х, взятое из промежутка знакопостоянства , обращает данное неравенство в ложное числовое неравенство. Например, при имеем ложное числовое неравенство .

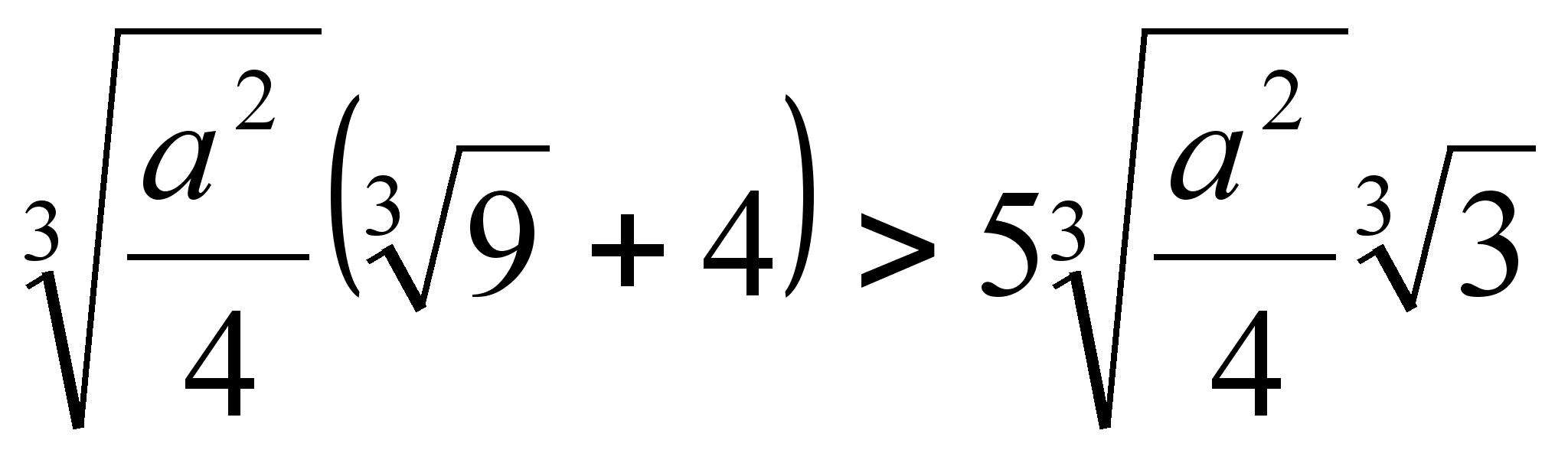Следовательно, промежуток не принадлежит решению.

Подставив, например, х = -а, взятое из промежутка знакопостоянства x . Значит, числовой промежуток x 0 решением неравенства является объединение двух числовых промежутков x .

б) если a и числовая ось разбивается на промежутки знакопостоянства . Как и в первом случае, устанавливаем, что данное неравенство тождественно истинное в промежутках и x > 0 и тождественно ложное в промежутке . Следовательно, при a и x > 0.

в) при а = 0 . Получим два промежутка знакопостоянства: x < 0 и x > 0, каждый из которых, как легко установить принадлежит решению.

Ответ: 1) при

2) при .

Пример 2. Решить неравенство

ОДЗ: 5^х – 7 ≥ 0

log₅7 ≤ x < +∞

Возводим обе части в квадрат:

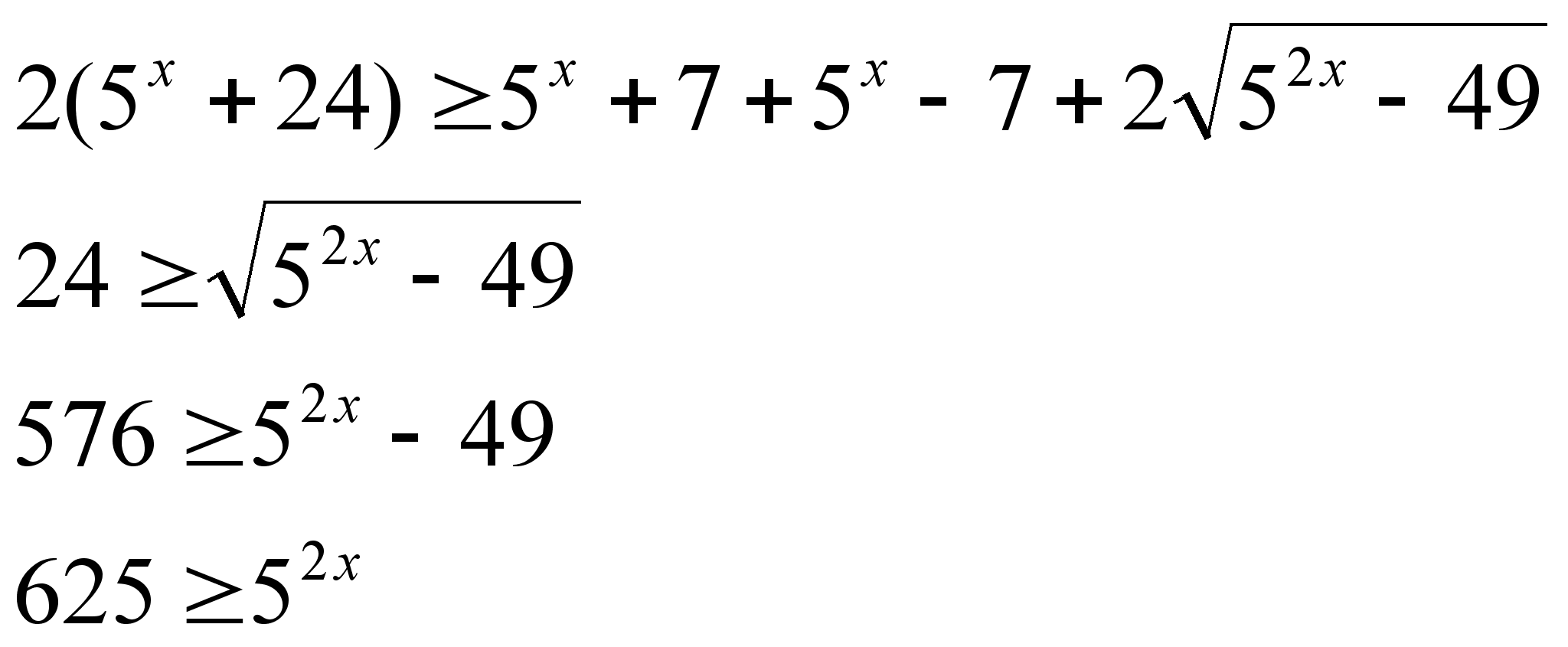
решением последнего неравенства является промежуток х ≤ 2. Учитывая ОДЗ получаем решение исходного неравенства log₅7 ≤ x ≤ 2.

Ответ: log₅7 ≤ x ≤ 2.

13. Подборка задач по теме «решение иррациональных неравенств».

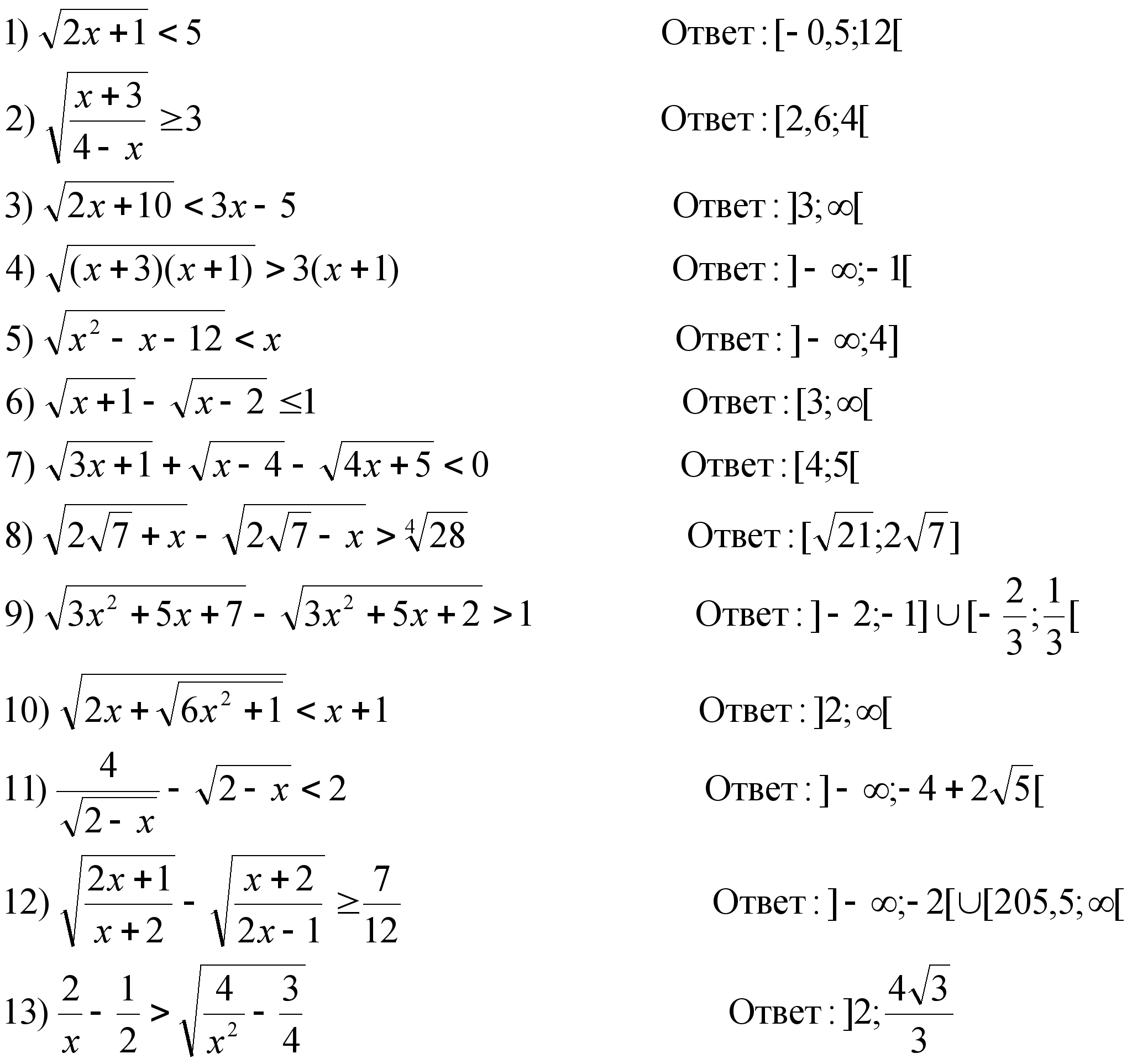
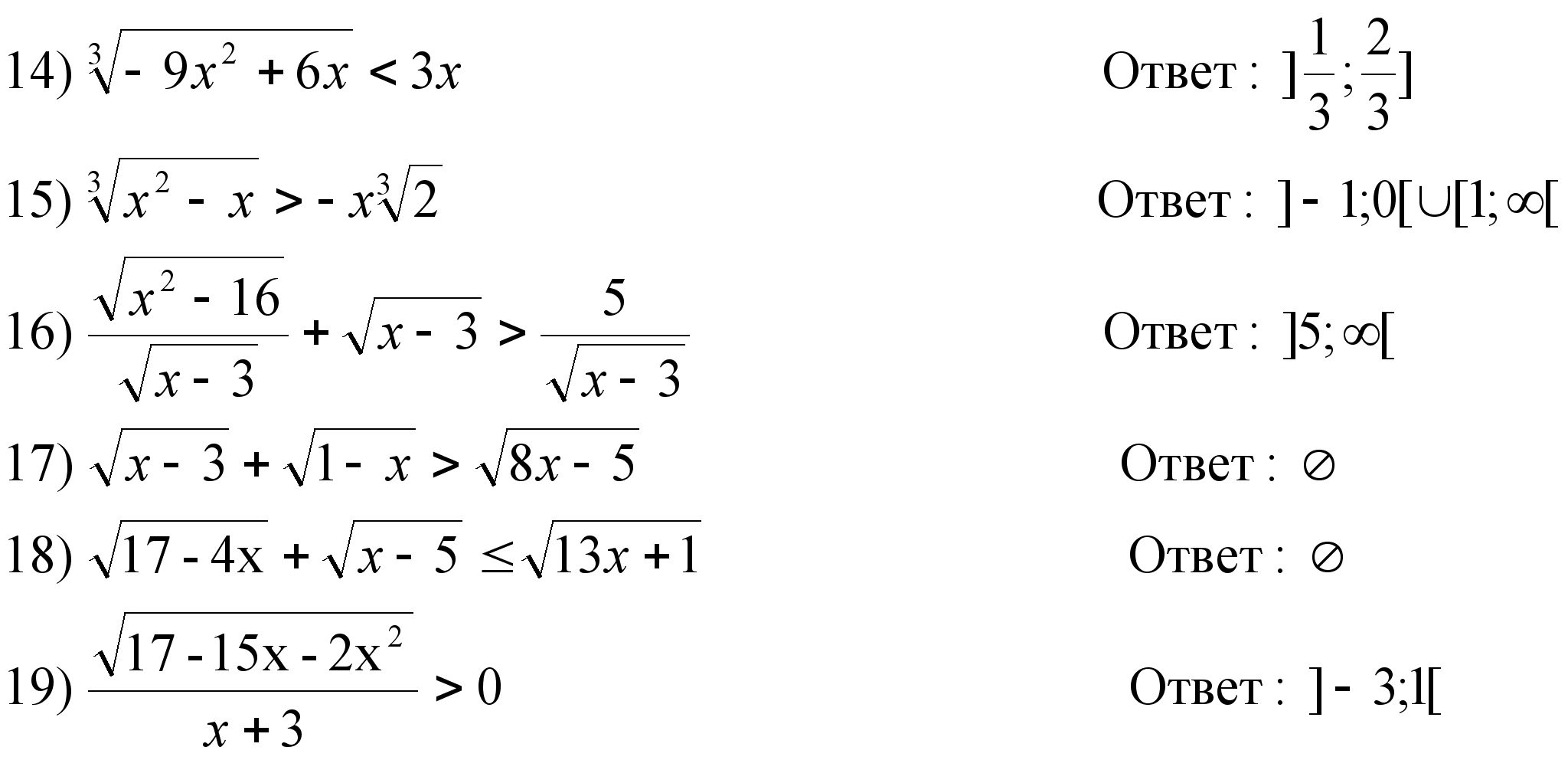
Похожие работы

Психолого-педагогическое обоснование внеклассной работы по математике

Скачать

113174

0

0

... говоря о том, что некоторые виды технических средств обладают исключительно большими возможностями наглядного показа материала обучения. Олимпиада одна из основных форм организации внеклассной работы по математике. Термин «олимпиада» проявился давно, хотелось бы вспомнить об истории отечественной математической олимпиады. Сначала о ней говорили в единственном числе, поскольку она организовывалась ...

Специальная педагогика

Скачать

899509

4

0

... и устойчивых требований, которые определяют характер и особенности организации коррекционно-образовательного процесса и управления познавательной деятельностью лиц с особыми образовательными потребностями. Специальная педагогика опирается на соответствующие обще- педагогические принципы организации образования и управления познавательной деятельностью, однако их реализация в системе специального ...

Исторические экскурсы в курсе алгебры 7 класса как средство развития познавательного интереса

Скачать

70672

3

3

... труде - все это формирует и развивает познавательный интерес и превращает его в важный стимул учебной деятельности учащихся [20,46]. Существуют различные средства развития познавательного интереса: решение занимательных, логических задач, игра, исторические экскурсы и другие. Наиболее подробно остановимся на исторических экскурсах. Знакомство с историей науки полезно для каждого человека, а для ...

Подготовка к Единому государственному экзамену по математике через элективные курсы

Скачать

45824

3

0

... учащихся к ЕГЭ, учителя математики СОШ №26 г.Якутска используют перечень вопросов содержания (кодификатор) школьного курса математики, усвоение которых проверяется при сдачи единого государственного экзамена 2007г. Элективный курс по подготовке к Единому Государственному Экзамену основан на повторении, систематизации и углублении знаний полученных ранее. Занятия проходят в форме свободного ...