Решение иррациональных неравенств, содержащих переменную под знаком двух и более радикалов четной степени

5. Решение иррациональных неравенств, содержащих переменную под знаком двух и более радикалов четной степени

Пусть дано иррациональное неравенство

(1)

В неравенстве (1) левые и правые части положительные, поэтому при возведении в четную степень эквивалентность не нарушается, если подкоренные выражения будут неотрицательны. Поэтому имеют место следующие эквивалентные преобразования:

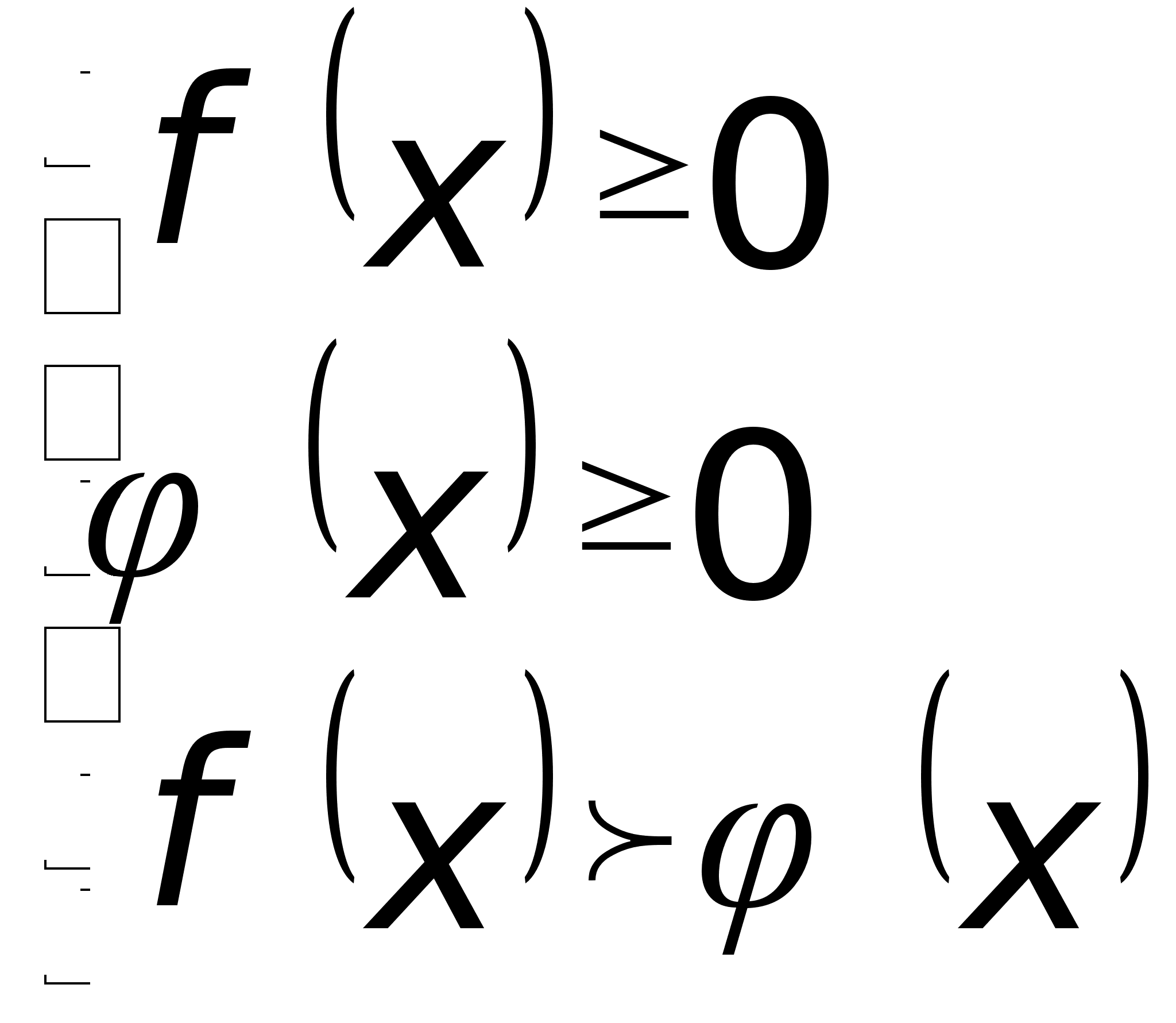(2)

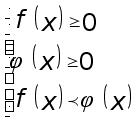(3)

Пример 1. Решить неравенство

Решение. Заменим данное неравенство эквивалентной системой неравенств

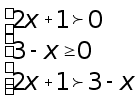
и далее

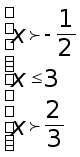
откуда получаем решение неравенства .

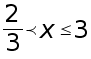Ответ: .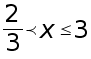

Пример 2. Решить неравенство

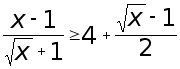
Решение. Предварительно упростим данное неравенство. умножив его на положительное выражение (т.к. мы рассматриваем всегда ). Проведем затем эквивалентные преобразования:

или

заменяем неравенство равносильной системой неравенств:

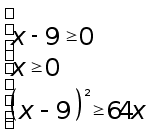
откуда получаем

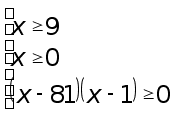
решением последнего неравенства системы является объединение и , а решением всей системы, а в силу равносильности проведенных преобразований и исходного неравенства, будет луч .

Ответ: .

Пример 3. Решить неравенство

Решение. Перепишем неравенство так, чтобы левая и правая его части были неотрицательными

всегда

и решим его, используя ранее рассмотренные эквивалентные преобразования:

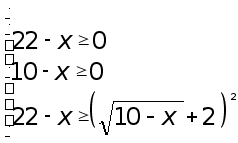
откуда получаем

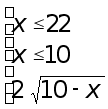
последнее неравенство системы является уже знакомым нам неравенством вида и решая его возведением в квадрат, получаем .

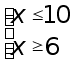
Ответ: .

Пример 4. Решим неравенство

Решение. Это неравенство равносильно следующей системе неравенств. где первые четыре неравенства являются ОДЗ

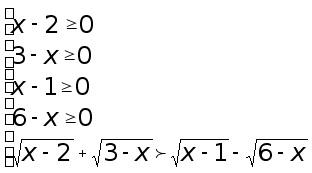
или

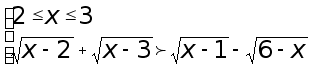
Так как , то , а потому . Далее , поэтому . Значит, , и тем более .

Но , следовательно. второе неравенство нашей системы выполняется при любых допустимых значения из ОДЗ исходного неравенства, т.е. система, а вместе с ней и исходное неравенство имеют решение .

Ответ: .

Пример 5. Решить неравенство

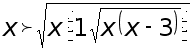
Решение. Правая часть данного неравенства неотрицательная, поэтому левая его часть должна быть положительной. В противном случае неравенство не имеет смысла. Учитывая это, проведем следующие эквивалентные преобразования:

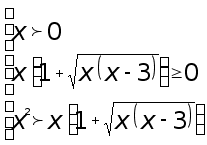
второе неравенство имеет смысл при любом из ОДЗ, т.е. при . если упростить третье неравенство системы, то получим

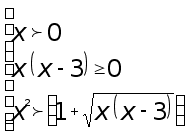
или

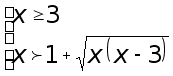
Последнее неравенство системы имеет положительную левую часть при , значим имеем право возвести неравенство в квадрат и затем легко решаем его, получаем

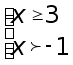
Ответ: .

Похожие работы

Психолого-педагогическое обоснование внеклассной работы по математике

Скачать

113174

0

0

... говоря о том, что некоторые виды технических средств обладают исключительно большими возможностями наглядного показа материала обучения. Олимпиада одна из основных форм организации внеклассной работы по математике. Термин «олимпиада» проявился давно, хотелось бы вспомнить об истории отечественной математической олимпиады. Сначала о ней говорили в единственном числе, поскольку она организовывалась ...

Специальная педагогика

Скачать

899509

4

0

... и устойчивых требований, которые определяют характер и особенности организации коррекционно-образовательного процесса и управления познавательной деятельностью лиц с особыми образовательными потребностями. Специальная педагогика опирается на соответствующие обще- педагогические принципы организации образования и управления познавательной деятельностью, однако их реализация в системе специального ...

Исторические экскурсы в курсе алгебры 7 класса как средство развития познавательного интереса

Скачать

70672

3

3

... труде - все это формирует и развивает познавательный интерес и превращает его в важный стимул учебной деятельности учащихся [20,46]. Существуют различные средства развития познавательного интереса: решение занимательных, логических задач, игра, исторические экскурсы и другие. Наиболее подробно остановимся на исторических экскурсах. Знакомство с историей науки полезно для каждого человека, а для ...

Подготовка к Единому государственному экзамену по математике через элективные курсы

Скачать

45824

3

0

... учащихся к ЕГЭ, учителя математики СОШ №26 г.Якутска используют перечень вопросов содержания (кодификатор) школьного курса математики, усвоение которых проверяется при сдачи единого государственного экзамена 2007г. Элективный курс по подготовке к Единому Государственному Экзамену основан на повторении, систематизации и углублении знаний полученных ранее. Занятия проходят в форме свободного ...