Решение иррациональных неравенств с параметрами

7. Решение иррациональных неравенств с параметрами

Параметром называют такую переменную, значения которой постоянны в пределах рассматриваемой задачи .

Значения параметров , для которых функции и определены, называются множеством допустимых значений параметров.

Неравенство, содержащее параметры, только тогда считается решенным, когда указано множество всех его решений при произвольной допустимой системе значений параметров. Решение параметрических иррациональных неравенств рассмотрим на примерах. Чтобы проанализировать все допустимые значения параметров и найти соответствующие искомые значения переменной, целесообразно данное неравенство заменить эквивалентной совокупностью неравенств, как это будет показано ниже на примерах.

Пример 1. Решить и исследовать неравенство:

(1)

Решение. Найдем ОДЗ неравенства (1) . Неравенство (1) заменим эквивалентной совокупностью неравенств

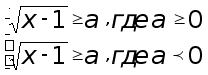
Ясно, что второе неравенство будет истинно при любом из ОДЗ, т.к. , . Первое неравенство совокупности имеет и правую и левую положительные части. Возведем в квадрат обе его части.

Все значения будут принадлежать ОДЗ, так как , значит .

Ответ: 1. ; 2. .

Пример 2. Решить неравенство

Решение. Легко видеть, что при данное неравенство не имеет решений, т.к. получаем положительную левую часть меньше отрицательно правой. что не имеет смысла. Рассмотрим неравенство при . ОДЗ неравенства

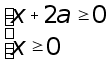
Неравенство имеет смысл лишь при . Получаем систему неравенств, эквивалентную исходному неравенству:

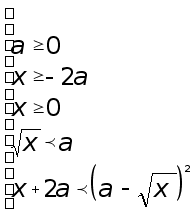
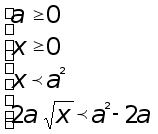
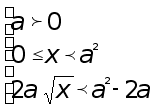
Решим последнее неравенство системы. Видим, что оно имеет смысл лишь при . Возведем в квадрат обе части неравенства

при

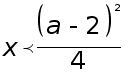
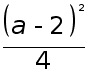Сравним и , чтобы определить верхнюю границу значений .

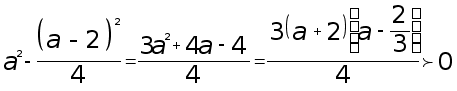
при значит >.

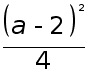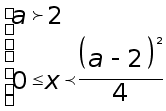
Ответ: если , то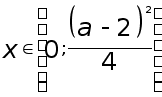

если . то .

Пример 3. Решить неравенство

Решение. Данное неравенство перепишем так

(1)

Легко видеть, что при а = 0 неравенство решения не имеет. Рассмотрим значение параметра а > 0 и а

неотрицательная, а правая отрицательная). Поэтому данное неравенство можно заменить следующей эквивалентной совокупностью систем неравенств:

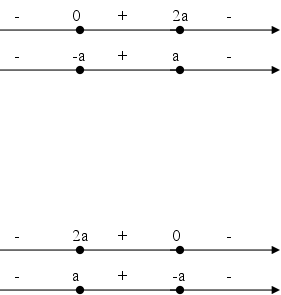
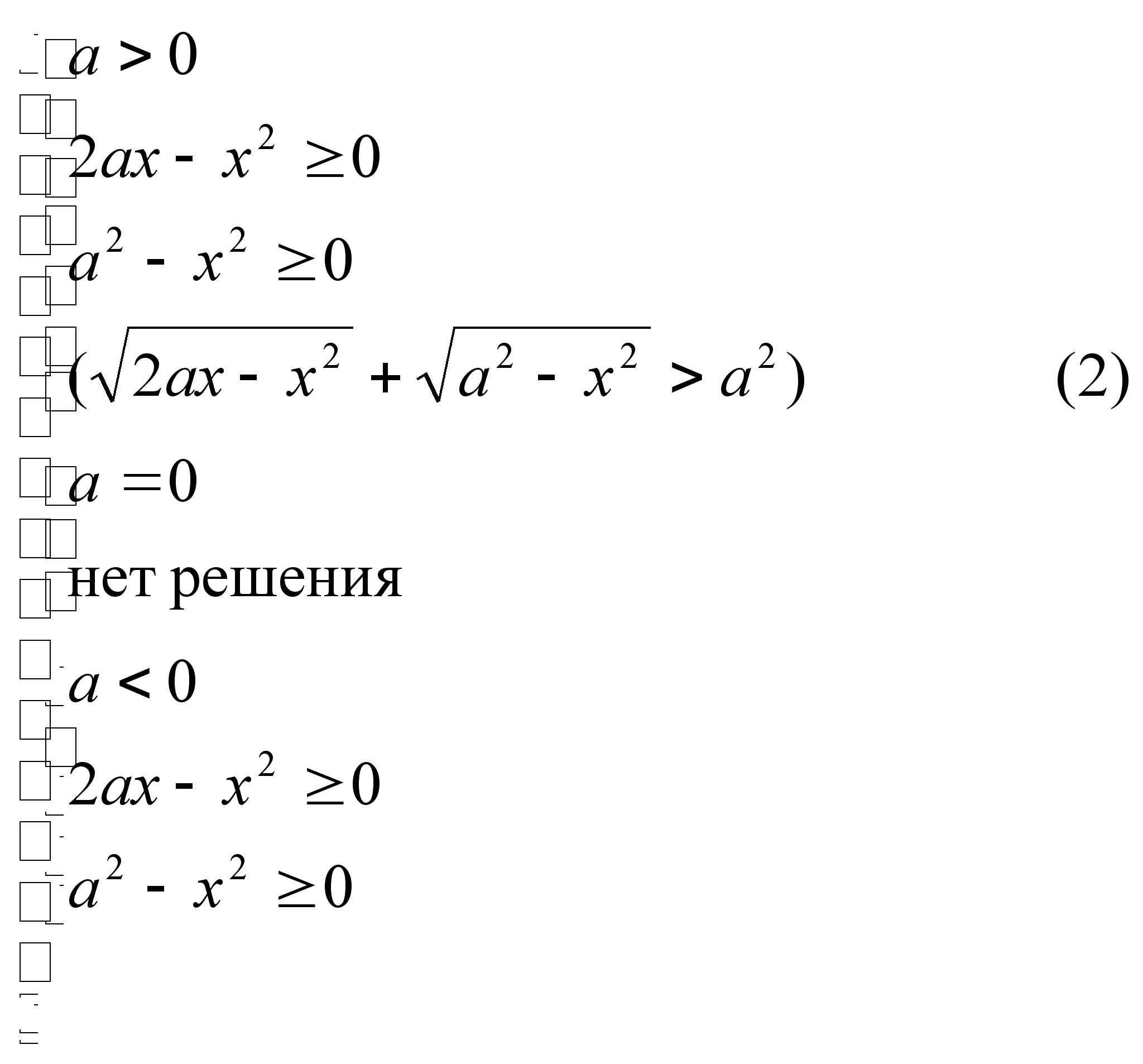
Рассмотрим неравенство (2). После выполнения преобразований получим:

При a > 0 значения х = а и х = 0 не удовлетворяют неравенству, а при всех значениях 0 < x < a указанное неравенство тождественно истинное, поэтому первая система совокупности эквивалентна системе:

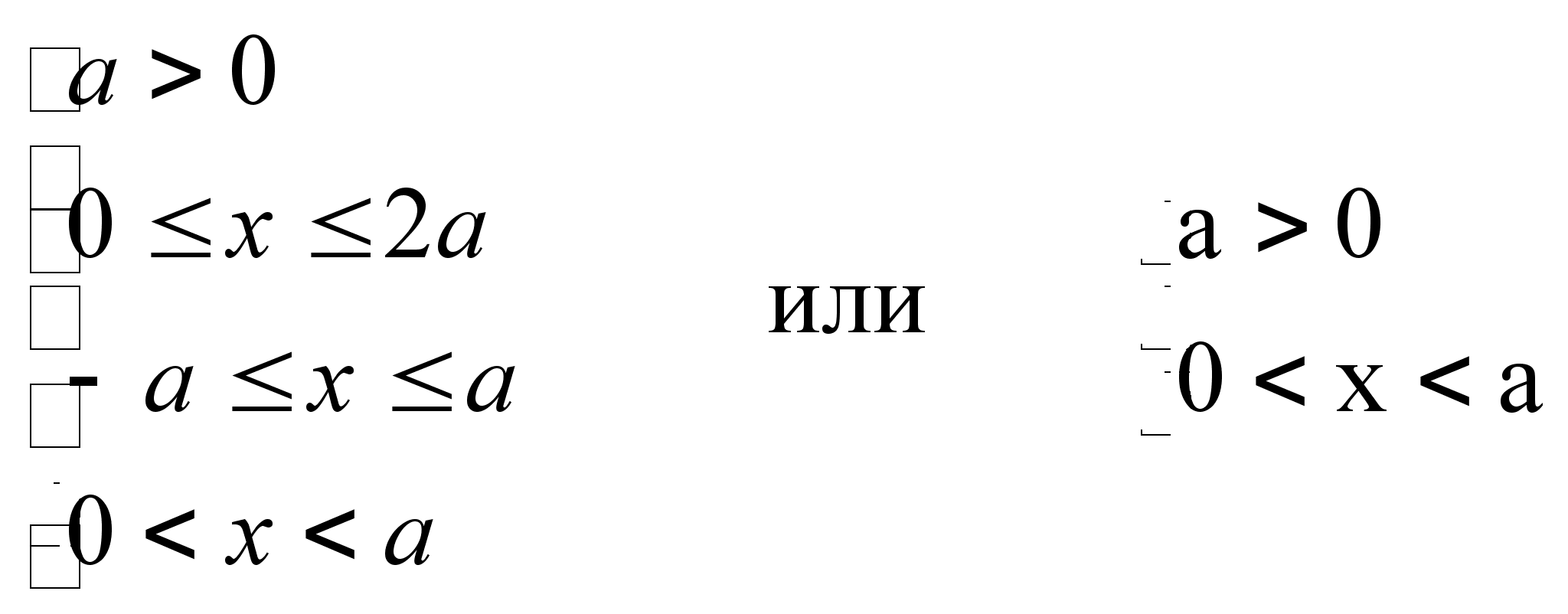
Итак, решение неравенства (1)

1) если а > 0 0 < x < a

2) если а = 0 нет решений

3) если a  x  0

Пример 4. Решить неравенство:

Решение. Возводим неравенство в квадрат. Так как левая и правая части неравенства неотрицательны, то эквивалентность не нарушается в области определения неравенства. Первый радикал имеет смысл при x  а, второй при x  b. При этих же значениях переменной имеет смысл и выражение, стоящее в правой части неравенства.

Итак,

равносильно системе

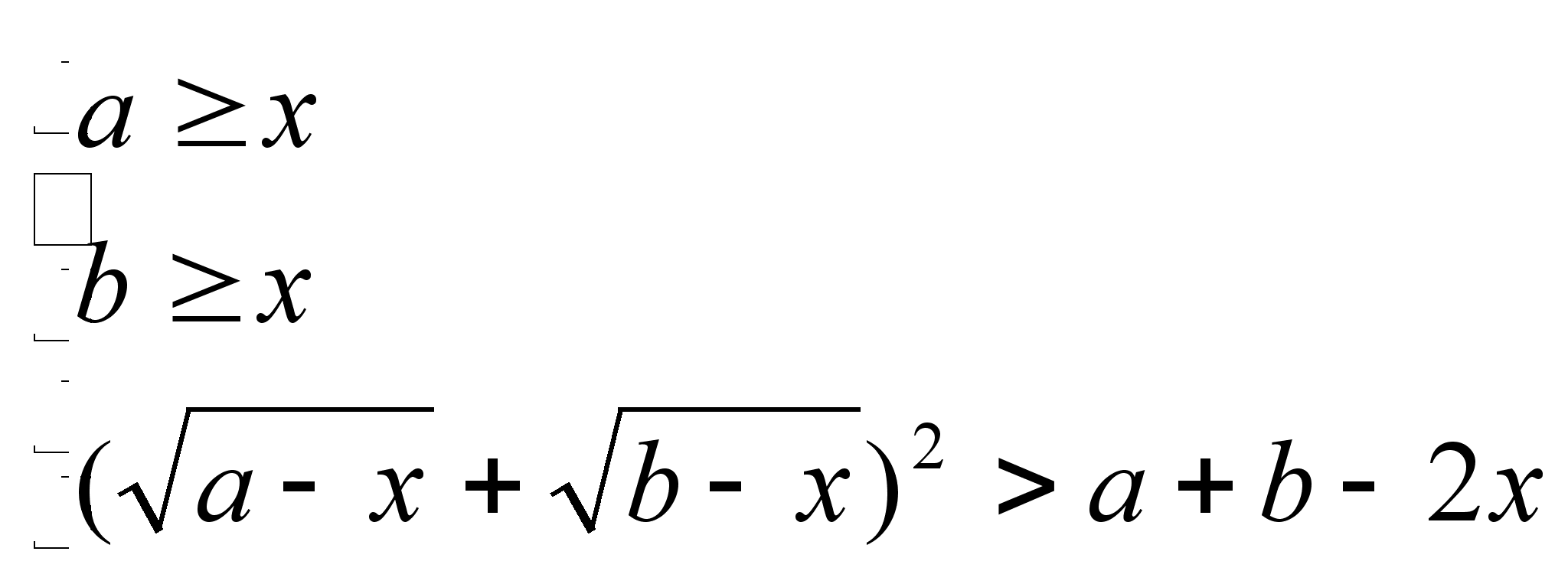
но

,

значит последнее неравенство системы равносильно неравенству:

или

А система равносильна системе

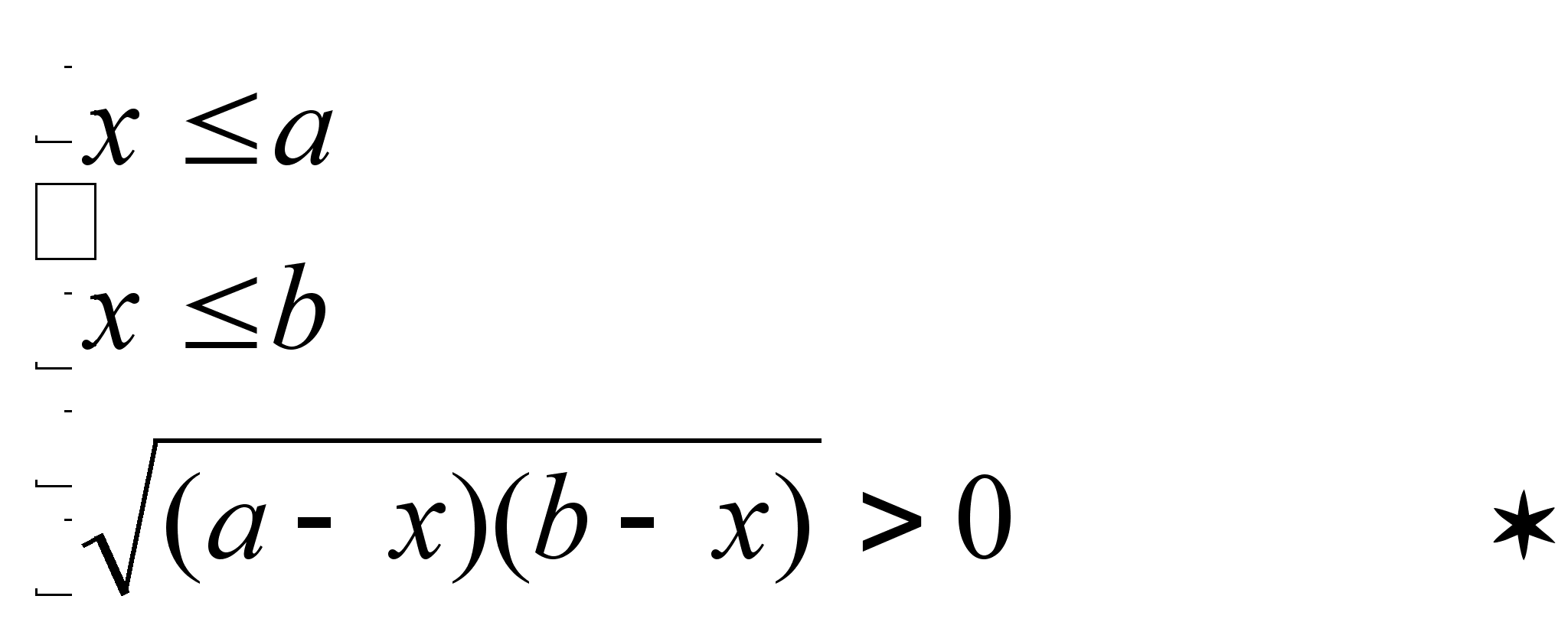
* выполняется, если оба множителя под корнем больше нуля или оба меньше нуля, значит наша система равносильна совокупности двух систем:

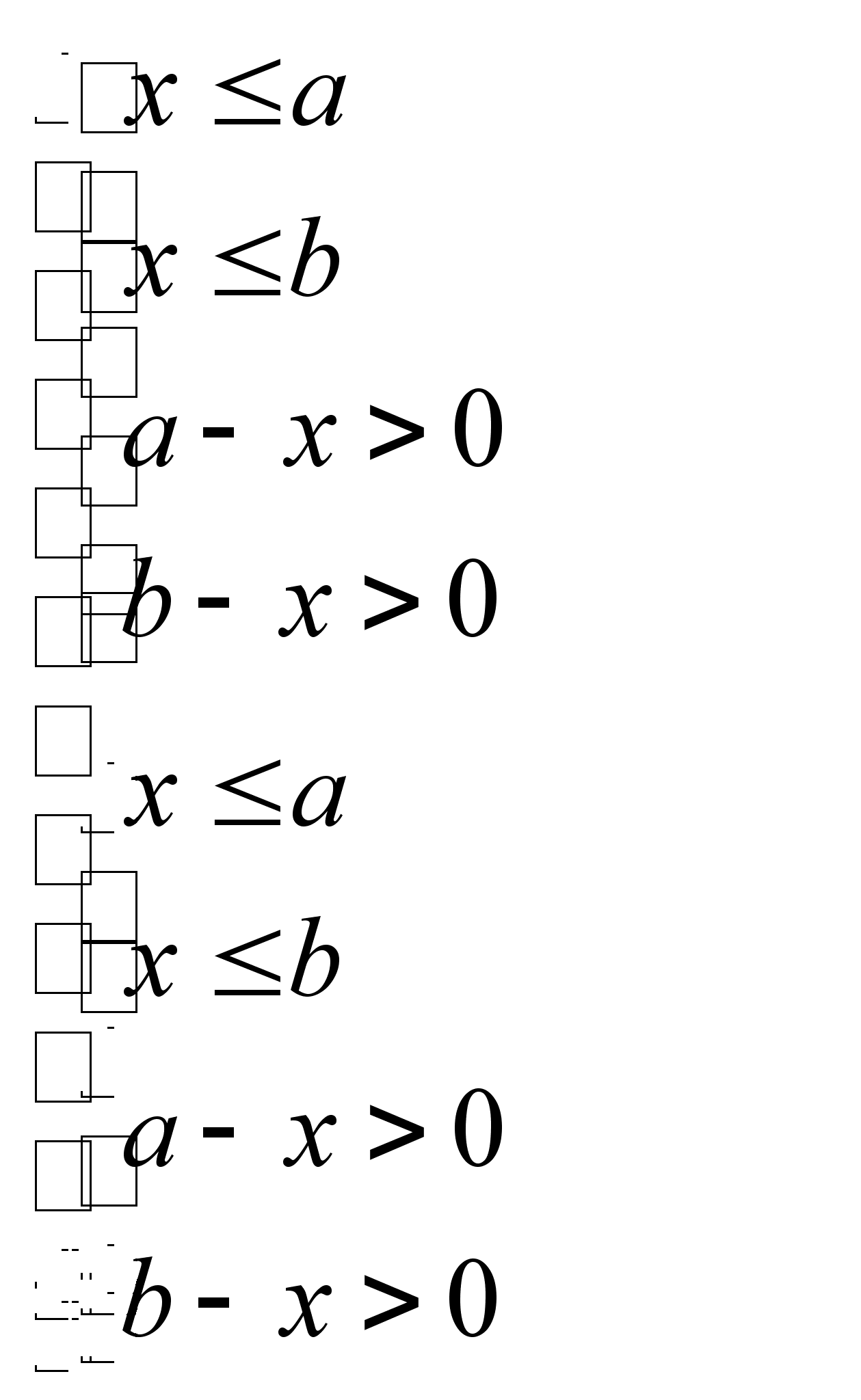
после выполнения преобразований получаем:

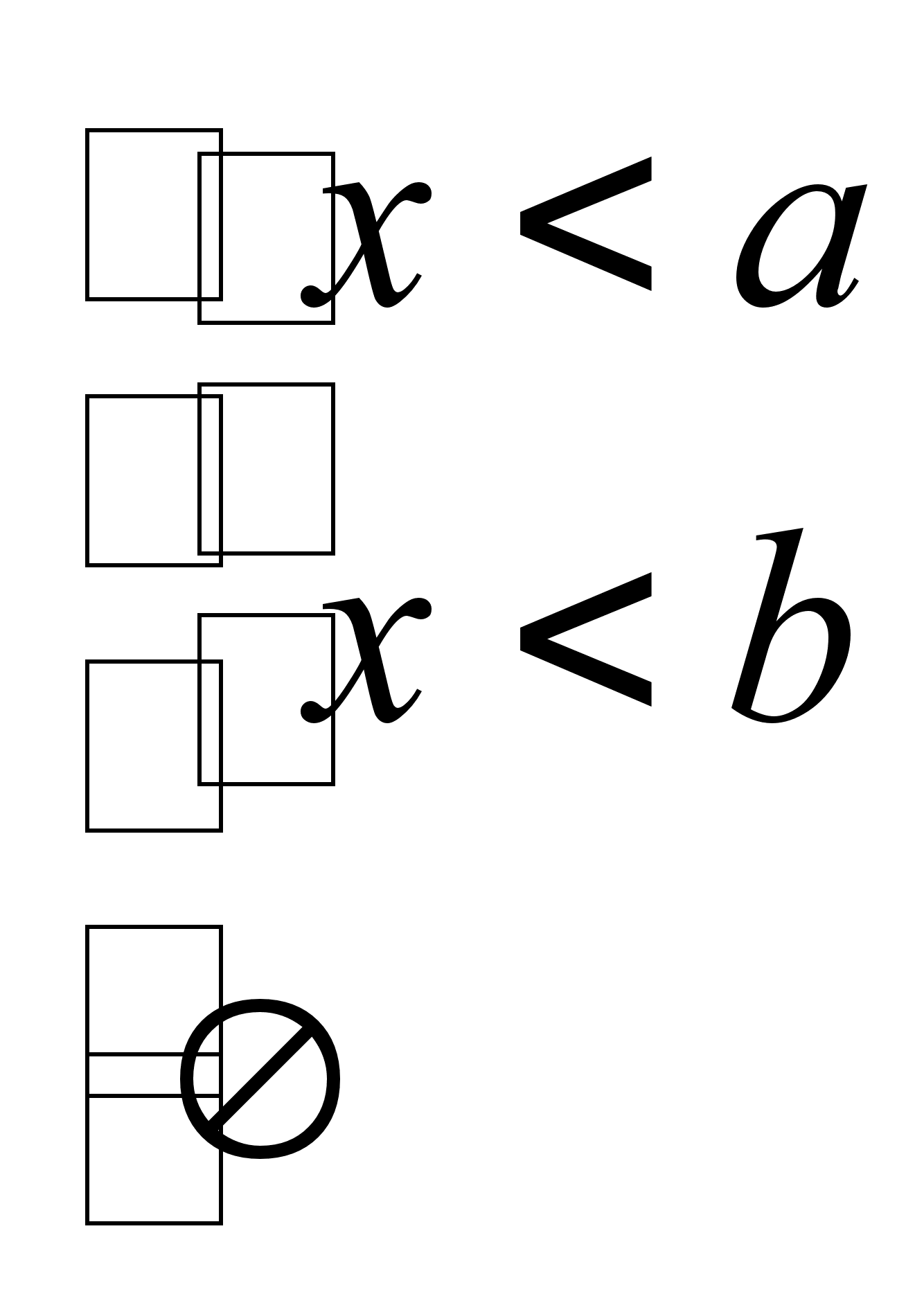
Видим, что в первой системе может быть два случая:

a  b,

b  a.

Ответ: 1) a  b x < b

2) a  b x < а

Похожие работы

Психолого-педагогическое обоснование внеклассной работы по математике

Скачать

113174

0

0

... говоря о том, что некоторые виды технических средств обладают исключительно большими возможностями наглядного показа материала обучения. Олимпиада одна из основных форм организации внеклассной работы по математике. Термин «олимпиада» проявился давно, хотелось бы вспомнить об истории отечественной математической олимпиады. Сначала о ней говорили в единственном числе, поскольку она организовывалась ...

Специальная педагогика

Скачать

899509

4

0

... и устойчивых требований, которые определяют характер и особенности организации коррекционно-образовательного процесса и управления познавательной деятельностью лиц с особыми образовательными потребностями. Специальная педагогика опирается на соответствующие обще- педагогические принципы организации образования и управления познавательной деятельностью, однако их реализация в системе специального ...

Исторические экскурсы в курсе алгебры 7 класса как средство развития познавательного интереса

Скачать

70672

3

3

... труде - все это формирует и развивает познавательный интерес и превращает его в важный стимул учебной деятельности учащихся [20,46]. Существуют различные средства развития познавательного интереса: решение занимательных, логических задач, игра, исторические экскурсы и другие. Наиболее подробно остановимся на исторических экскурсах. Знакомство с историей науки полезно для каждого человека, а для ...

Подготовка к Единому государственному экзамену по математике через элективные курсы

Скачать

45824

3

0

... учащихся к ЕГЭ, учителя математики СОШ №26 г.Якутска используют перечень вопросов содержания (кодификатор) школьного курса математики, усвоение которых проверяется при сдачи единого государственного экзамена 2007г. Элективный курс по подготовке к Единому Государственному Экзамену основан на повторении, систематизации и углублении знаний полученных ранее. Занятия проходят в форме свободного ...