Решение простейших иррациональных неравенств

4. Решение простейших иррациональных неравенств

Если иррациональное неравенство содержит один радикал, то всегда можно привести его к равносильному неравенству, в котором радикал будет находиться в одной части неравенства, а все другие члены неравенства - в другой его части, то есть неравенству вида или , где и - рациональные алгебраические выражения относительно переменной . Привидение иррационального неравенства, содержащего один радикал к виду

(1)

или

(2),

называется уединением радикала.

Разобьем простейшие неравенства на две группы:

I – неравенства, содержащие радикал четной степени, т.е. .

II - неравенства, содержащие радикал нечетной степени, т.е. .

I. Рассмотрим решение неравенств вида (1). Ясно, что всякое решение этого неравенства является в то же время решением неравенства (при этом условии имеет смысл левая часть неравенства) и решением неравенства (поскольку ). Значит, неравенство

(3)

равносильно системе неравенств:

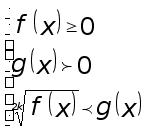
где и следствия неравенства (3). Так как в области, определяемой первыми двумя неравенствами этой системы, обе части третьего неравенства системы определены и принимают только неотрицательные значения, то их возведение в квадрат на указанном множестве есть равносильное преобразование неравенства. В результате получаем, что неравенство (3) равносильно системе неравенств:

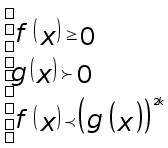
Таким образом, мы вывели теорему о решении неравенств вида (3).

Теорема 1. Неравенство вида равносильно системе неравенств:

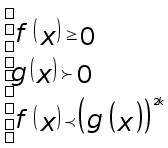
Аналогично для неравенств вида .

Теорема 2. Неравенство вида равносильно системе неравенств

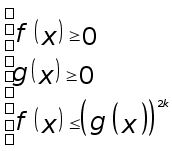
Рассмотрим теперь неравенства вида (2), т.е.

(4)

Оно равносильно системе

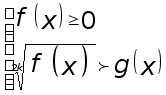(5)

Но в отличие от неравенства (3) может здесь принимать как положительные, так и отрицательные значения. Поэтому, рассмотрев систему (5) в каждом из двух случаев и , получим совокупность систем:

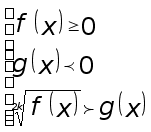
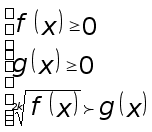
В первой их этих систем последнее неравенство можно опустить как следствие двух первых неравенств. Во второй системе обе части последнего неравенства можно возвести в квадрат (так как обе его части положительны).

Итак, неравенство (4) равносильно совокупности двух систем неравенств

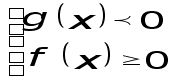
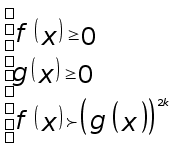
Заметим, что второе неравенство второй системы можно опустить - оно является следствием последнего неравенства системы.

Теорема 3. Неравенство вида равносильно совокупности двух систем неравенств

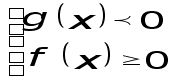
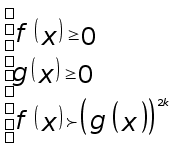
Аналогично.

Теорема 4. Неравенство вида равносильно совокупности двух систем неравенств

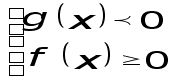
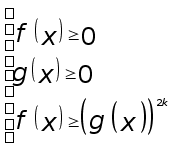
Неравенства вида , , , являются частными случаями рассмотренных выше неравенств, когда .

Пример 1. Решим неравенство

Решение. Заданное неравенство - неравенство вида (3), поэтому по теореме 1 оно равносильно системе неравенств:

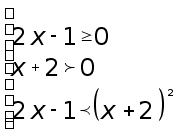
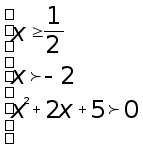
Так как квадратный трехчлен имеет отрицательный дискриминант и положительный старший коэффициент, то он положителен при всех значениях . Поэтому решения последней системы таковы: .

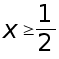Ответ: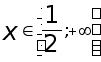

Пример 2. Решить неравенство

Решение. По теореме 3 наше неравенство эквивалентно совокупности систем неравенств

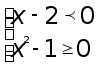
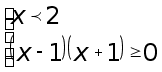
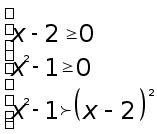
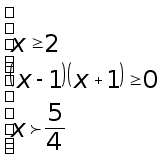
Применим метод интервалов для решения последней конструкции неравенств.

Решение первой системы:

Второй:

Получаем совокупность

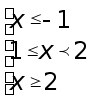
Ответ: и .

Пример 3. Решить неравенство

Решение. По теореме 1 наше неравенство эквивалентно системе

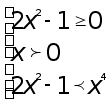
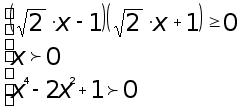
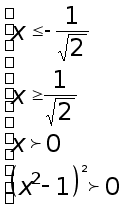
Последнее неравенство системы выполняется всегда. если и .

Итак, решением неравенства является 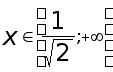исключая .

Ответ: .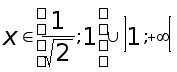

II. Рассмотрим теперь неравенства, содержащие радикал нечетной степени, т.е. . Решение также проводится также путем последовательного возведения обеих частей неравенства в соответствующую степень и преобразования его в неравенство, не содержащее радикалов. При возведении неравенства в нечетную степень эквивалентность не нарушается. Имеют место следующие эквивалентные преобразования:

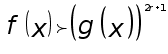
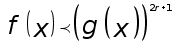
При при возведении в степень знак не изменится, т.к. 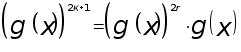, 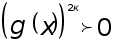. Значит 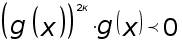при .

может быть любое, т.к. под знаком радикала нечетной степени может стоять как отрицательная, так и положительная функция.

Пример 4. Решить неравенство

Решение. Возведем в куб обе части неравенства:

или

Решим полученное неравенство методом интервалов

Ответ: .

Похожие работы

Психолого-педагогическое обоснование внеклассной работы по математике

Скачать

113174

0

0

... говоря о том, что некоторые виды технических средств обладают исключительно большими возможностями наглядного показа материала обучения. Олимпиада одна из основных форм организации внеклассной работы по математике. Термин «олимпиада» проявился давно, хотелось бы вспомнить об истории отечественной математической олимпиады. Сначала о ней говорили в единственном числе, поскольку она организовывалась ...

Специальная педагогика

Скачать

899509

4

0

... и устойчивых требований, которые определяют характер и особенности организации коррекционно-образовательного процесса и управления познавательной деятельностью лиц с особыми образовательными потребностями. Специальная педагогика опирается на соответствующие обще- педагогические принципы организации образования и управления познавательной деятельностью, однако их реализация в системе специального ...

Исторические экскурсы в курсе алгебры 7 класса как средство развития познавательного интереса

Скачать

70672

3

3

... труде - все это формирует и развивает познавательный интерес и превращает его в важный стимул учебной деятельности учащихся [20,46]. Существуют различные средства развития познавательного интереса: решение занимательных, логических задач, игра, исторические экскурсы и другие. Наиболее подробно остановимся на исторических экскурсах. Знакомство с историей науки полезно для каждого человека, а для ...

Подготовка к Единому государственному экзамену по математике через элективные курсы

Скачать

45824

3

0

... учащихся к ЕГЭ, учителя математики СОШ №26 г.Якутска используют перечень вопросов содержания (кодификатор) школьного курса математики, усвоение которых проверяется при сдачи единого государственного экзамена 2007г. Элективный курс по подготовке к Единому Государственному Экзамену основан на повторении, систематизации и углублении знаний полученных ранее. Занятия проходят в форме свободного ...