Самостоятельная
работа учащихся
- один из важнейших
способов организации
познавательной
деятельности
Фронтальная
и групповая
формы организации
познавательной
деятельности
учащихся
Изучение
учебных возможностей
учащихся. Методика
проведения
факультативных
занятий
Результаты
опытно-экспериментальной
работы
Архимед
установил
неравенства
Решение
простейших
иррациональных
неравенств
Решение
иррациональных
неравенств,
содержащих
переменную
под знаком двух
и более радикалов
четной степени
Решение
иррациональных
неравенств,
содержащих
переменную
под знаком двух
и более радикалов
нечетной степени
Решение
иррациональных
неравенств
с параметрами
Решение
иррациональных
неравенств,
способом введения
новой переменной
Способ
домножения
обеих частей
иррационального
неравенства
на некоторое
число, либо
выражение
Решение
иррациональных
неравенств
путем проб,
выводов
Классические
неравенства
Группа повторяет
пройденный
материал
Группа повторяет
изученное
Группа на примерах
рассматривает
решение иррациональных
неравенств
с параметрами
Группа подбирает
и решает неравенства
по теме «Решение
иррациональных
неравенств»
способом введения
новой переменной»
Навигация
Группа повторяет изученное
Организация познавательной деятельности учащихся на факультативных занятиях по теме Иррациональные неравенства
107387
знаков
6
таблиц
244
изображения
2 группа повторяет изученное.
Занятие №4.
Тема: Решение иррациональных неравенств, содержащих переменную под знаком двух и более радикалов четной степени.
Цель: отработка навыков решения иррациональных неравенств, содержащих переменную под знаком двух и более радикалов четной степени.
Учащиеся из 1 группы у доски рассказывают новый материал, объясняют неравенства, которые они решили дома, с помощью учителя разбираются непонятные места.
Делаем вывод: при возведении таких неравенств в четную степень эквивалентность не нарушается только тогда, когда обе части неравенства неотрицательны. Некоторые неравенства следует сначала привести к такому виду, когда ясно видно, что обе части его неотрицательны.
Решим пример (кто-то из ребят 2 группы решает у доски).
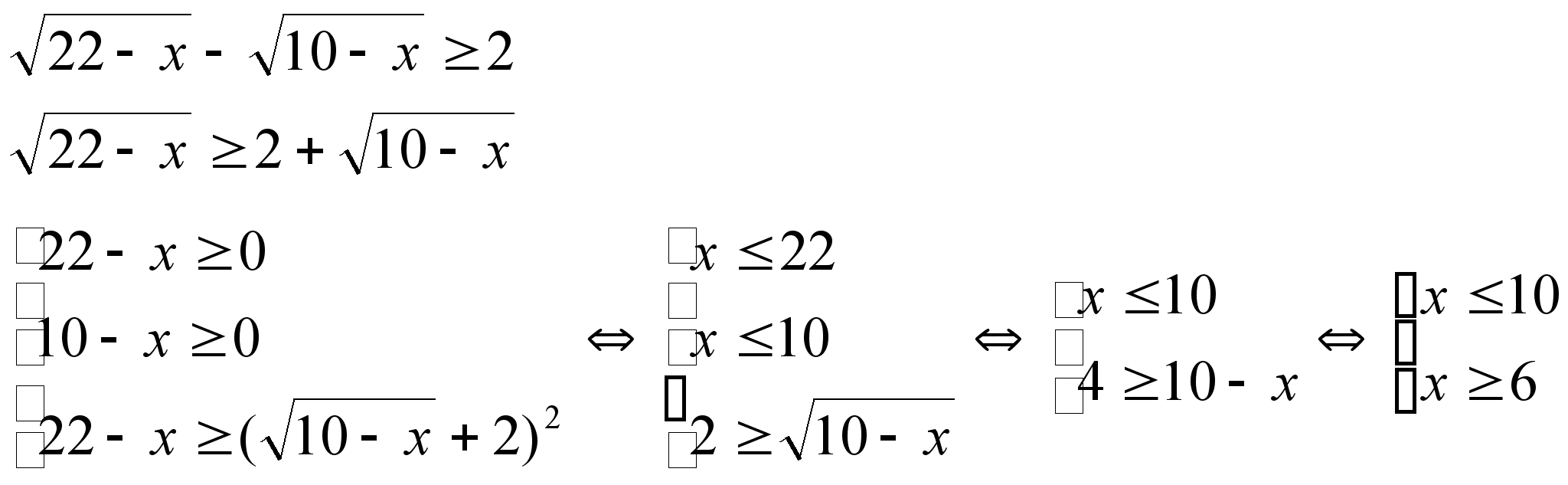
Ответ: 
Решить неравенства
1)
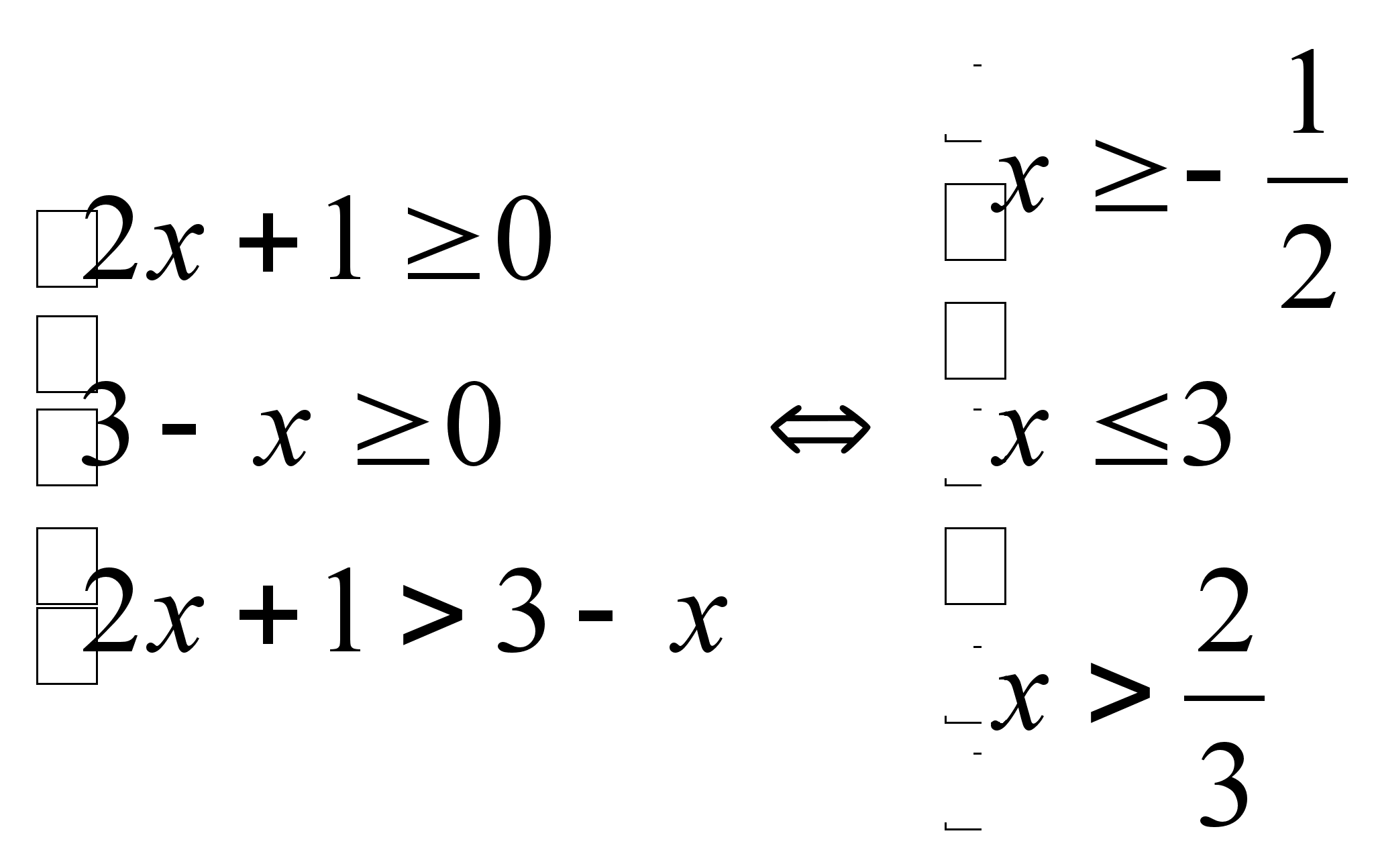
Ответ: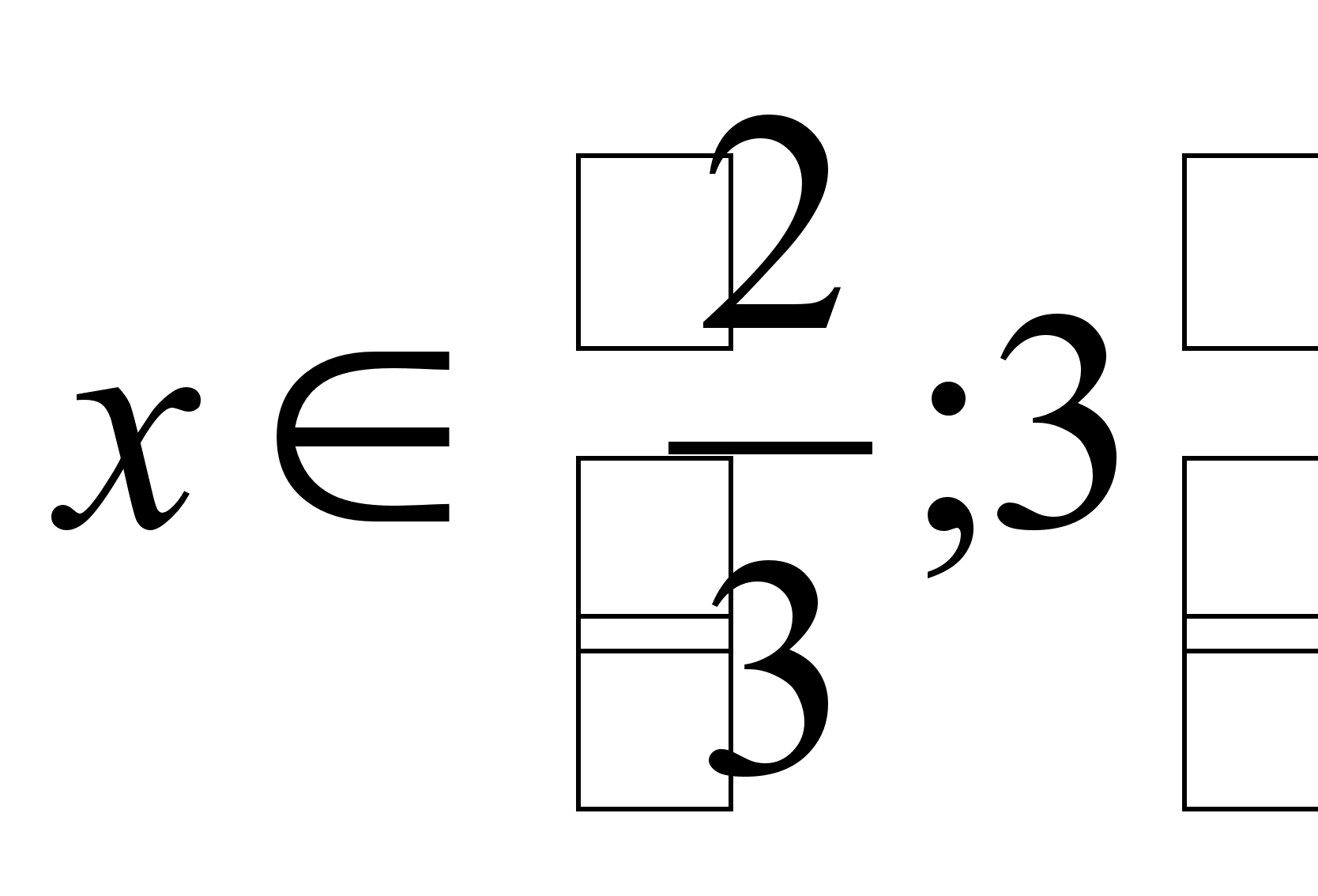 
2)
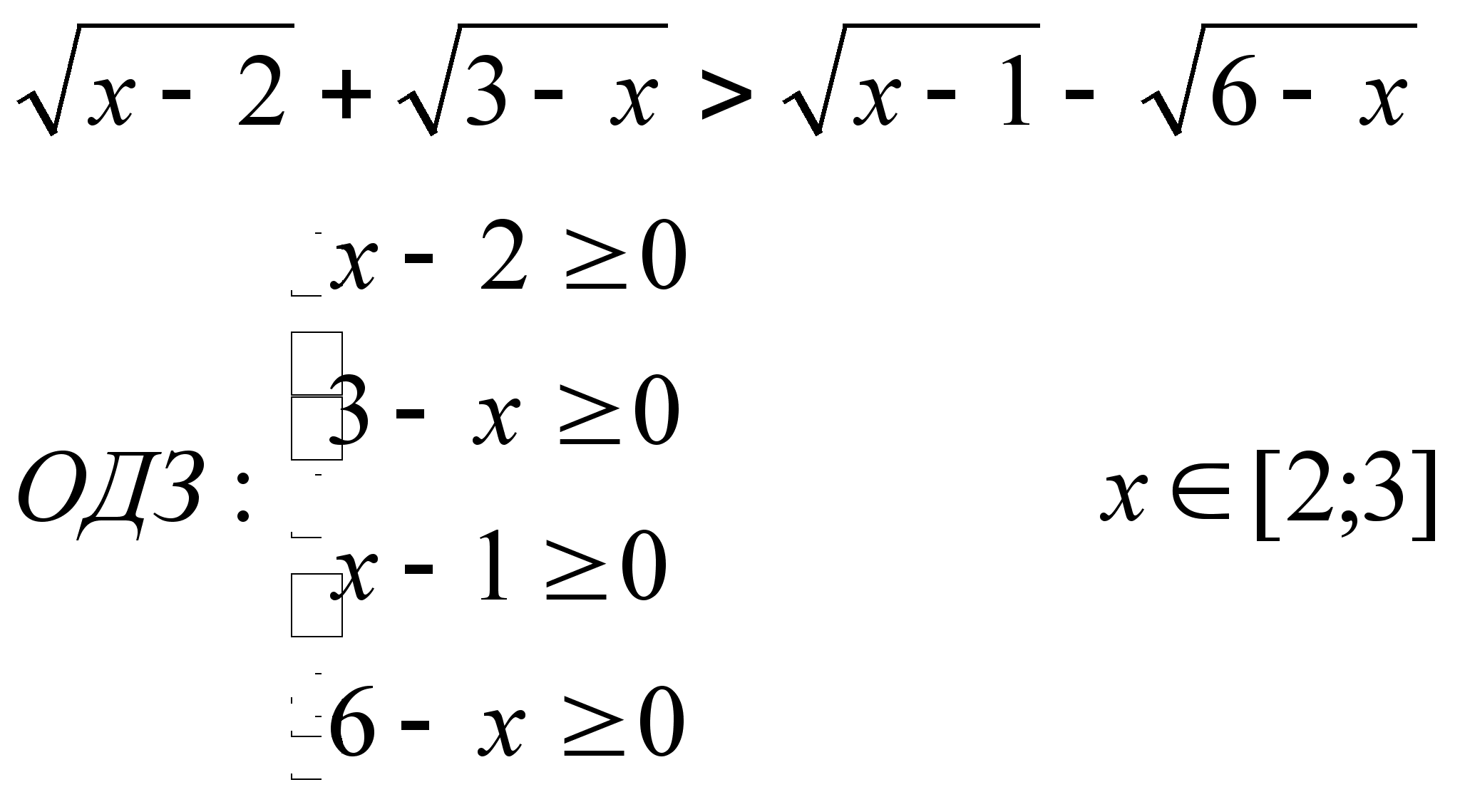
На ОДЗ 
Значит неравенство истинно.
Ответ: 
3)
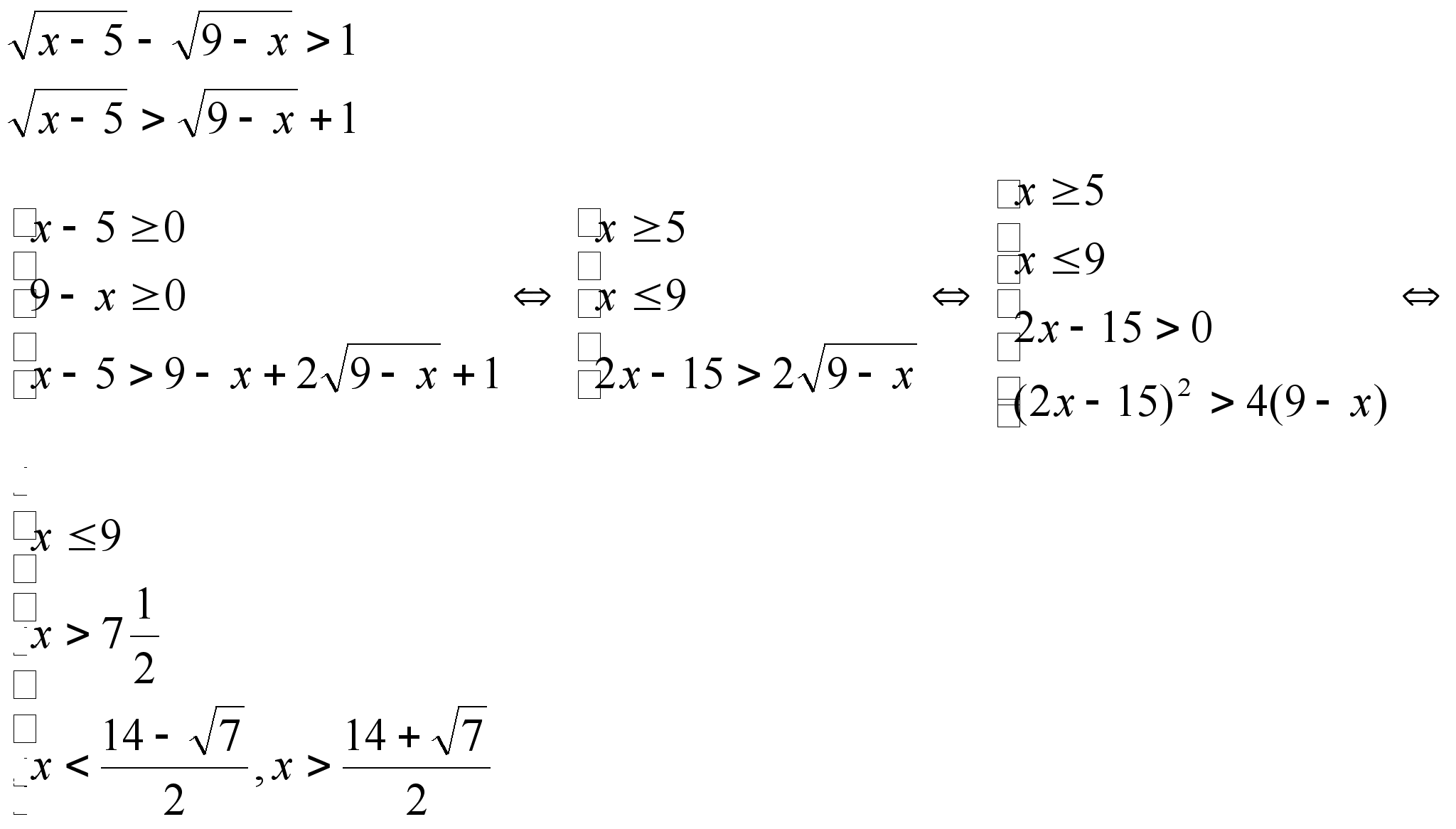Ответ:
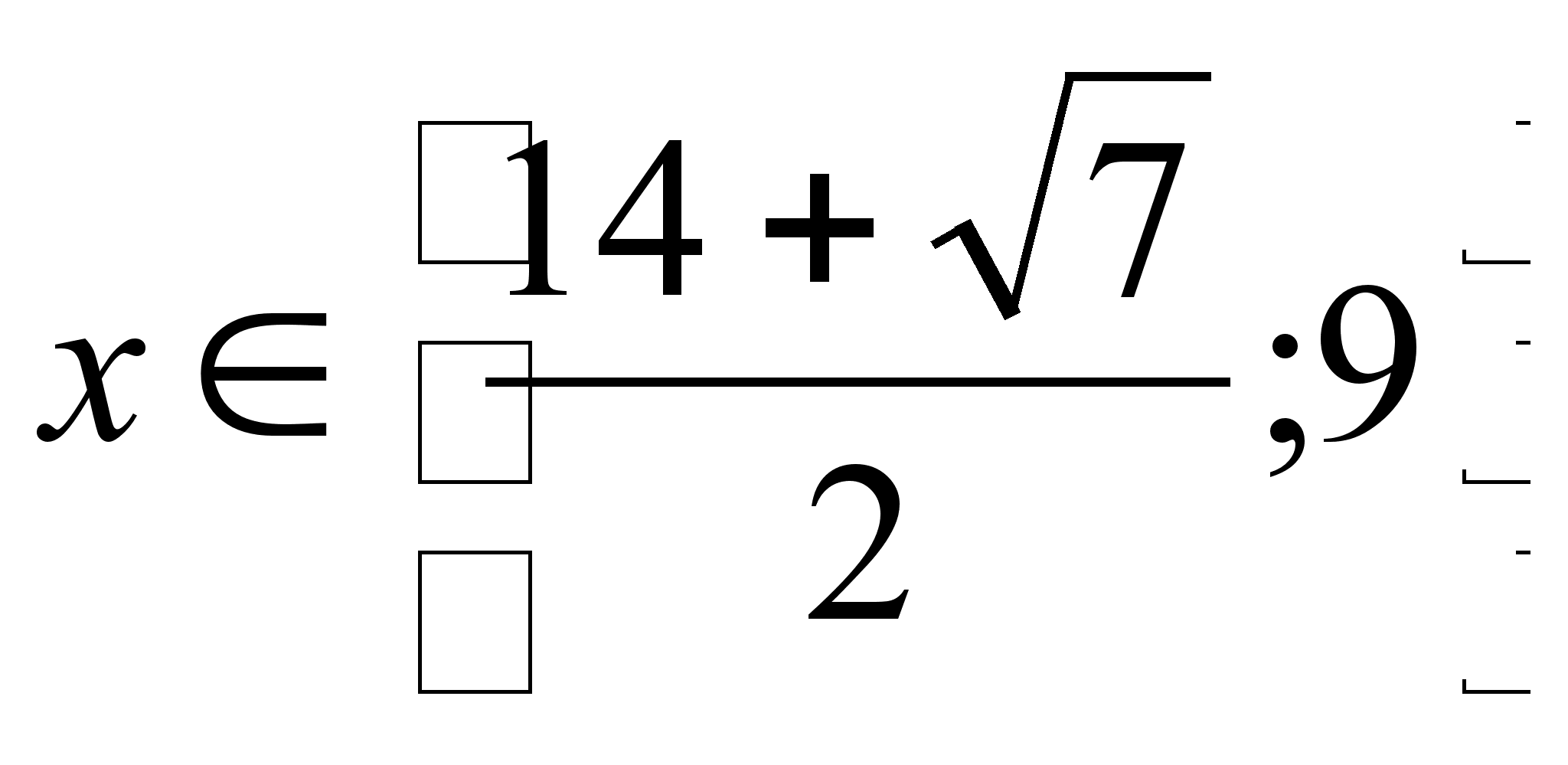
4) 
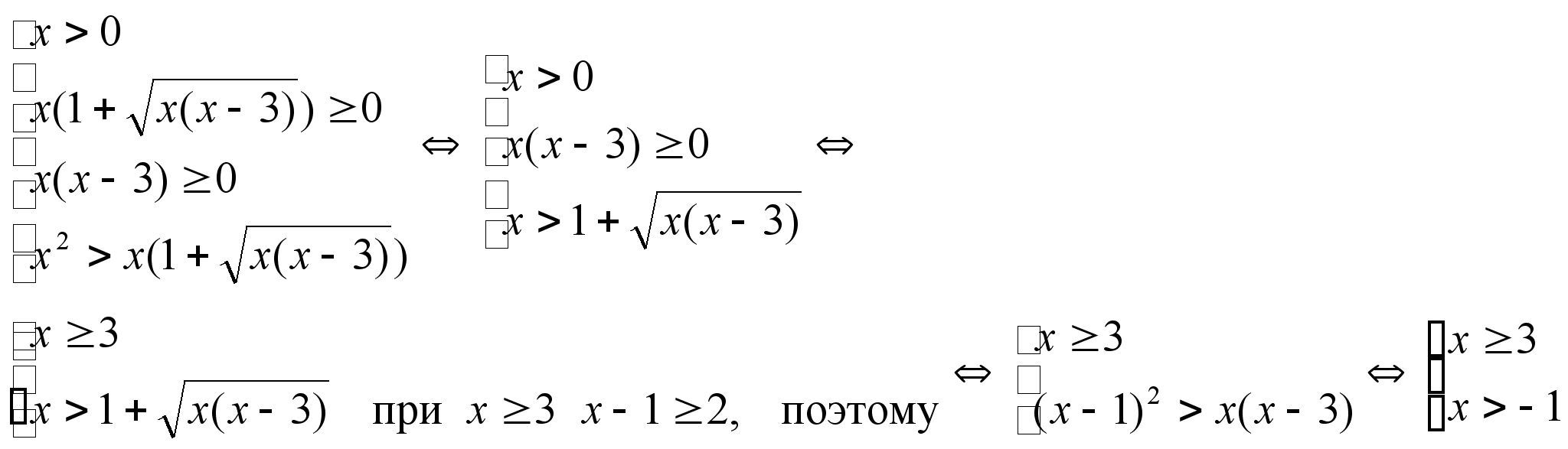
Ответ: 
5)
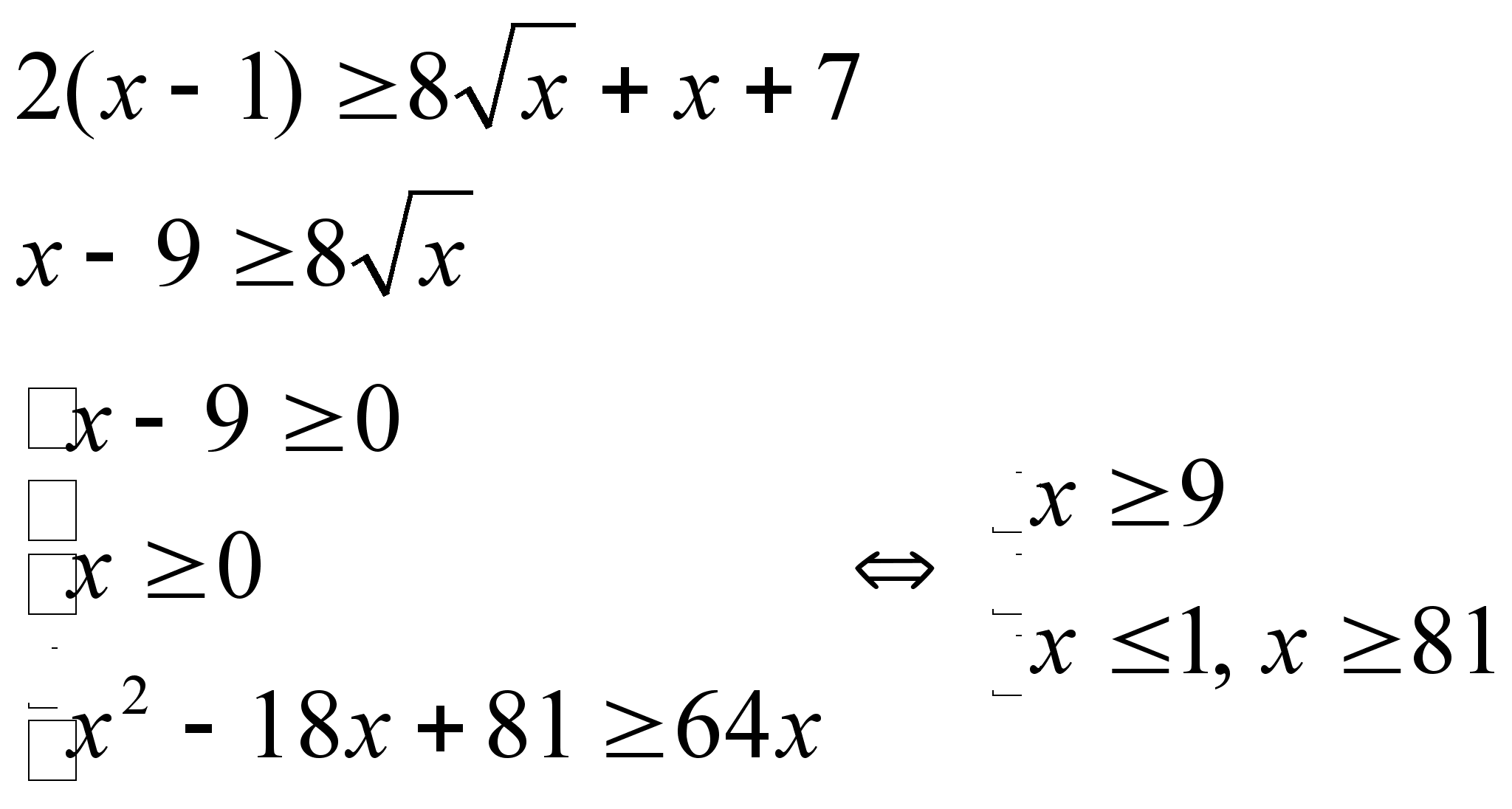
Ответ: 
6)
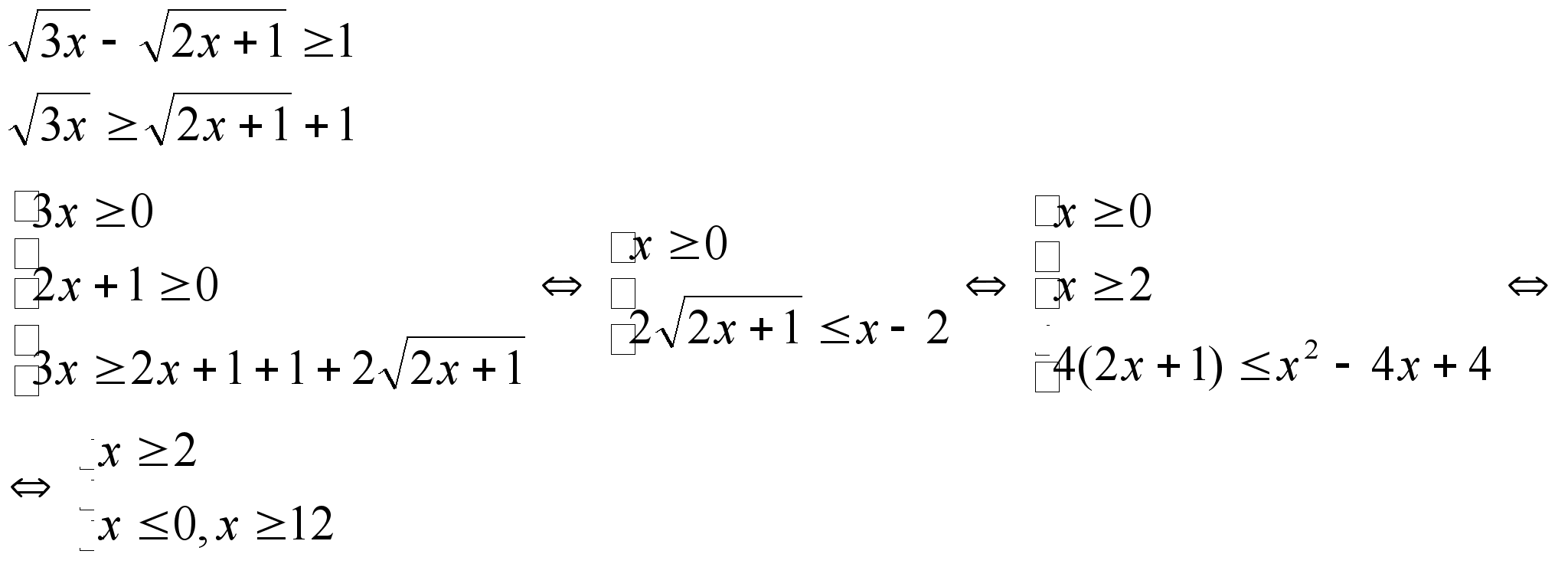
Ответ:
7) 
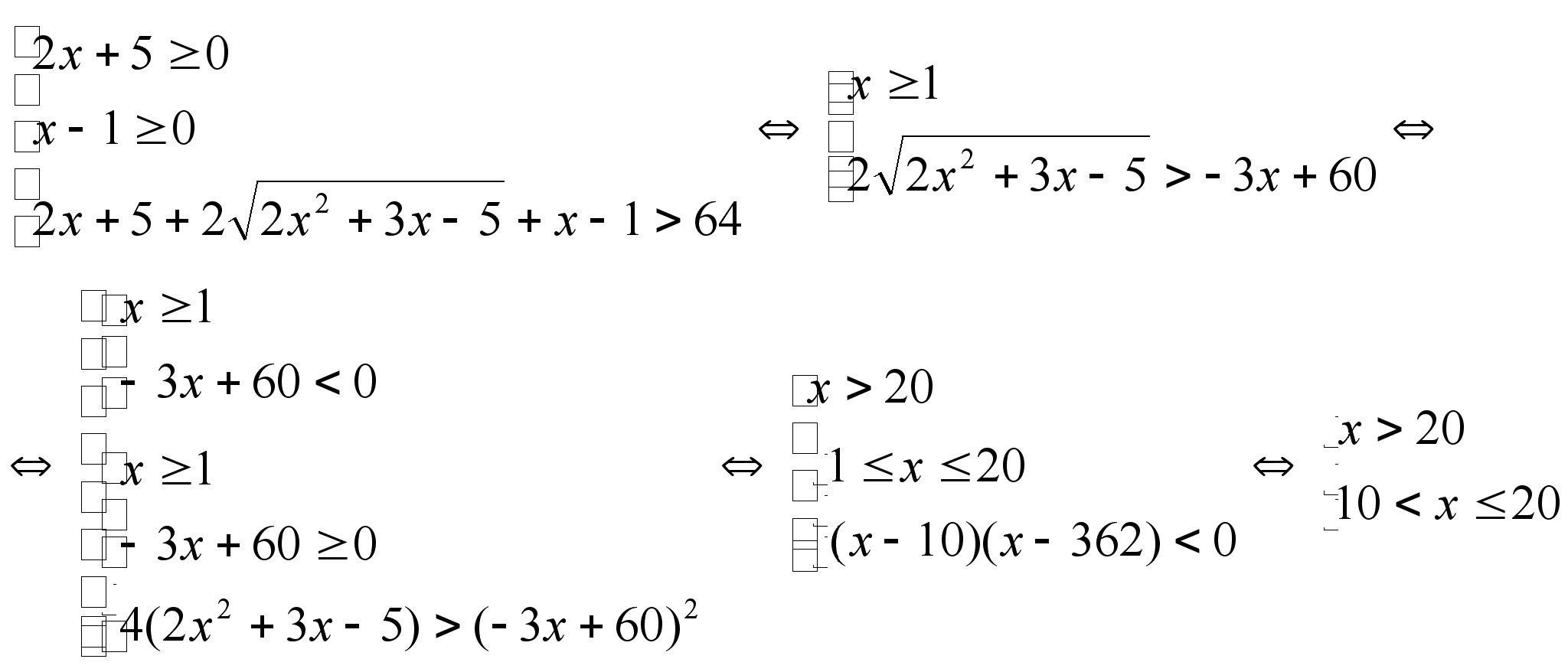
Ответ: 
IV. Д/з
1 группа пишет доклады по теме: «Решение иррациональных неравенств, содержащих переменную под знаком двух и более радикалов нечетной степени». Особое внимание обратить на решение неравенств вида:
и неравенств,
содержащих
радикалы третьей
и второй степени.
2 группа:
повторение,
решить неравенства
а)
;
б)
Занятие №5
Тема: решение иррациональных неравенств, содержащих переменную под знаком двух и более радикалов нечетной степени.
Цель: познакомить учащихся с неравенствами, содержащими переменную под знаком двух и более радикалов нечетной степени и показать способы их решения.
I. Проверка Д/з 2 группы (устно)
II. Учащиеся 1 группы читают доклады, объясняют у доски решенные неравенства. Все остальные ребята с учителем разбирают решения.
III. Решить неравенства (решения проверить друг у друга в парах).
1)
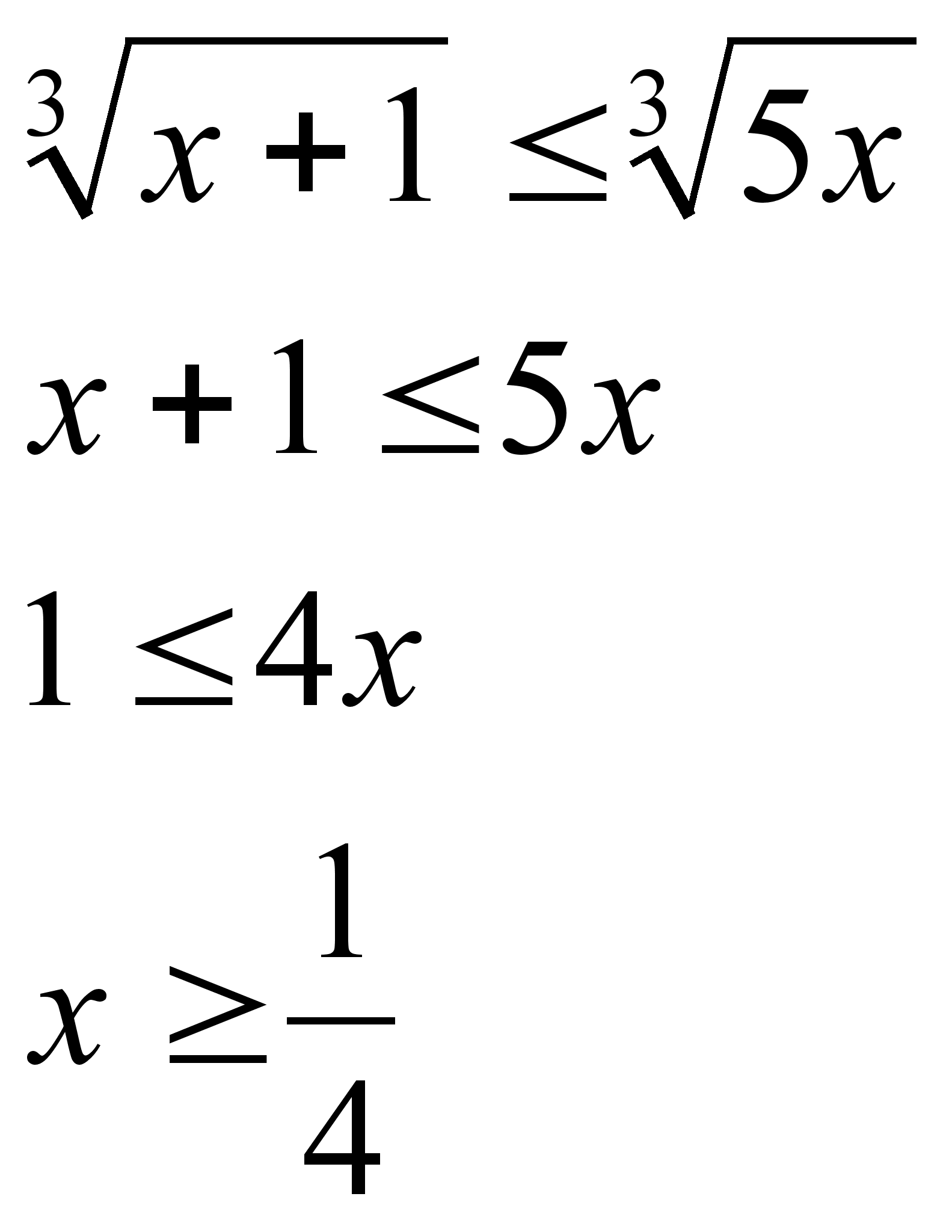
Ответ: 
2)
+ - +
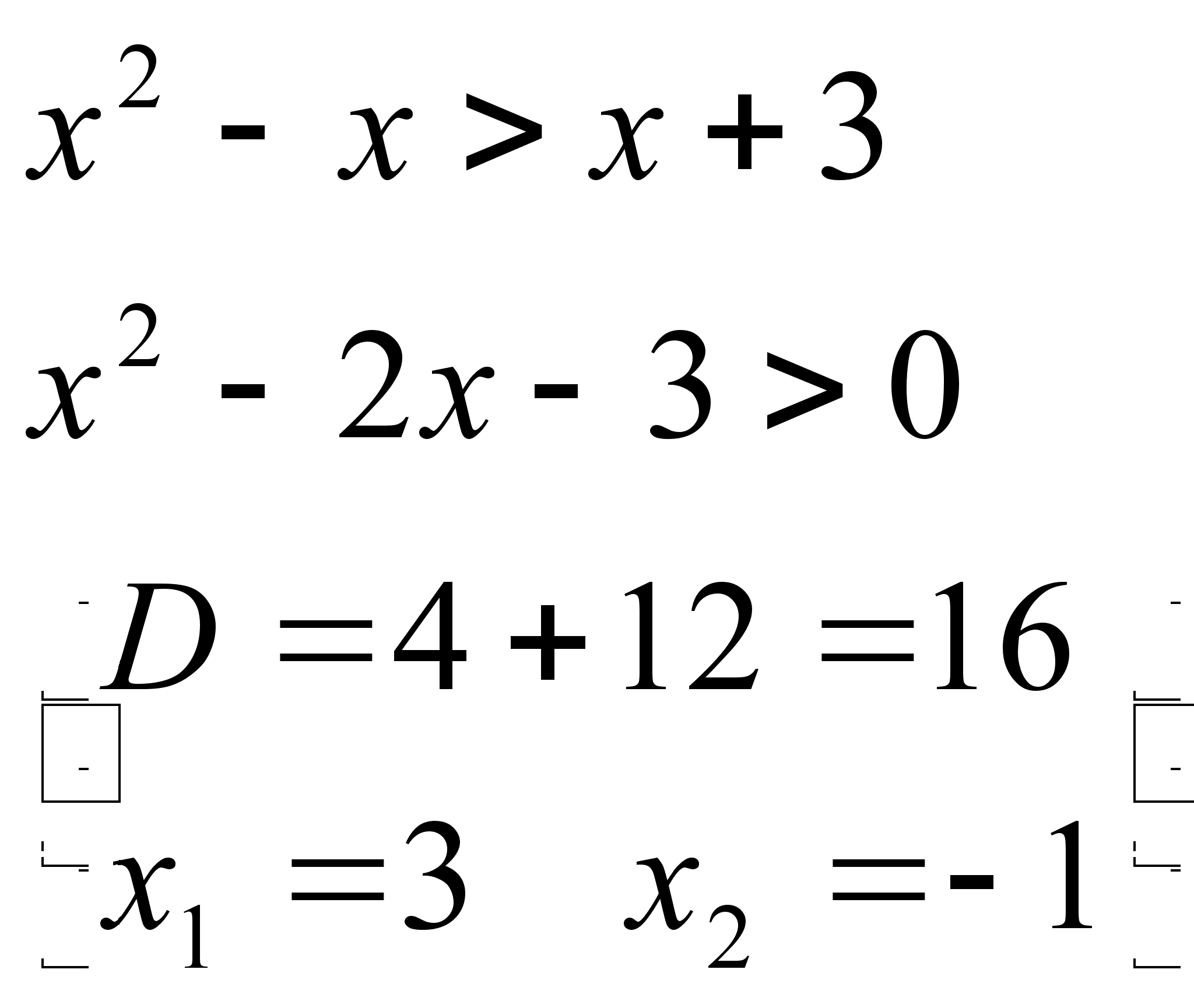
-1 3
Ответ: 
3) 
найдем решение соответствующего уравнения:
возводим в куб
делаем замену
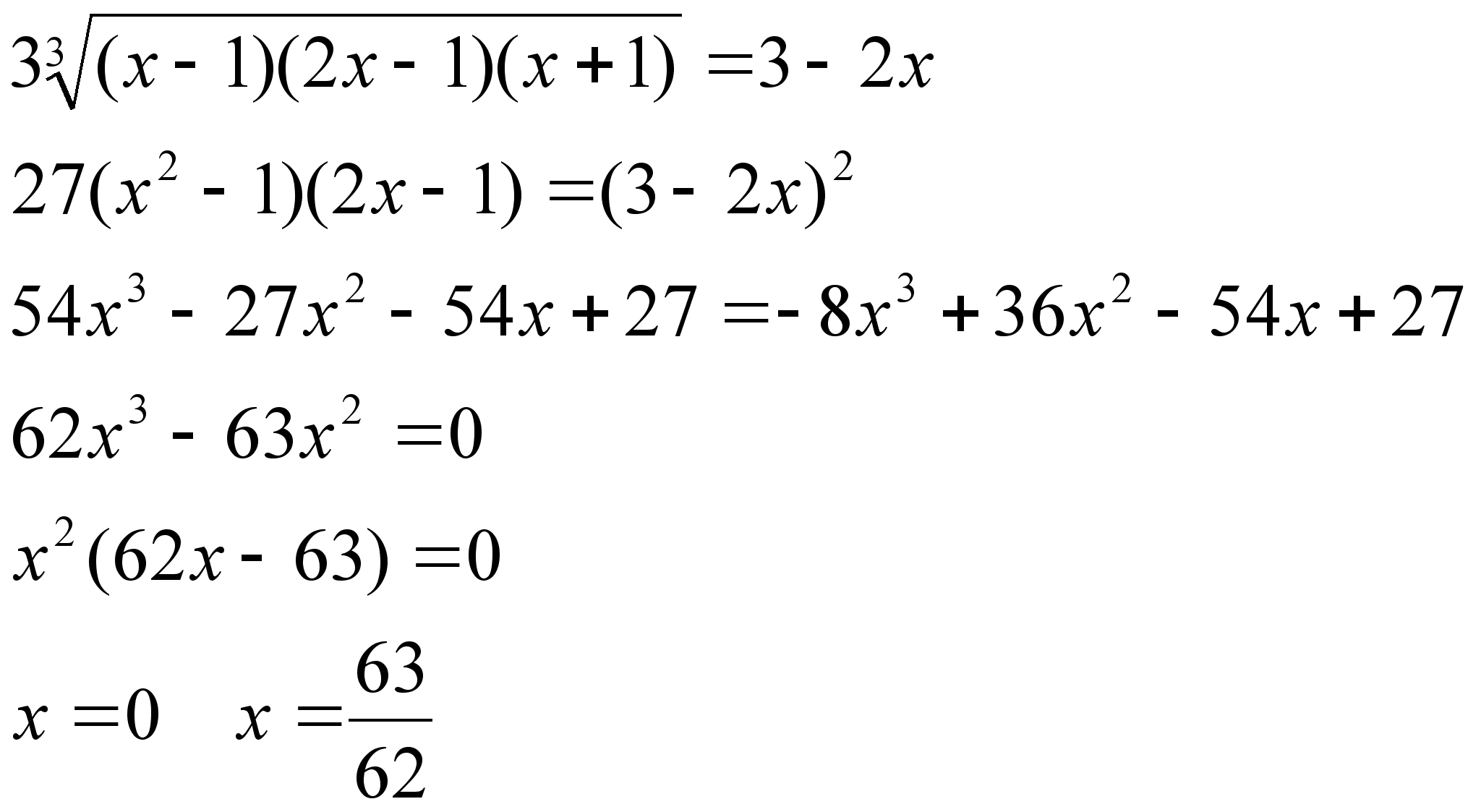
Проверка:
1. 
-2=1 – ложно, корень х = 0 – посторонний
2.
- +
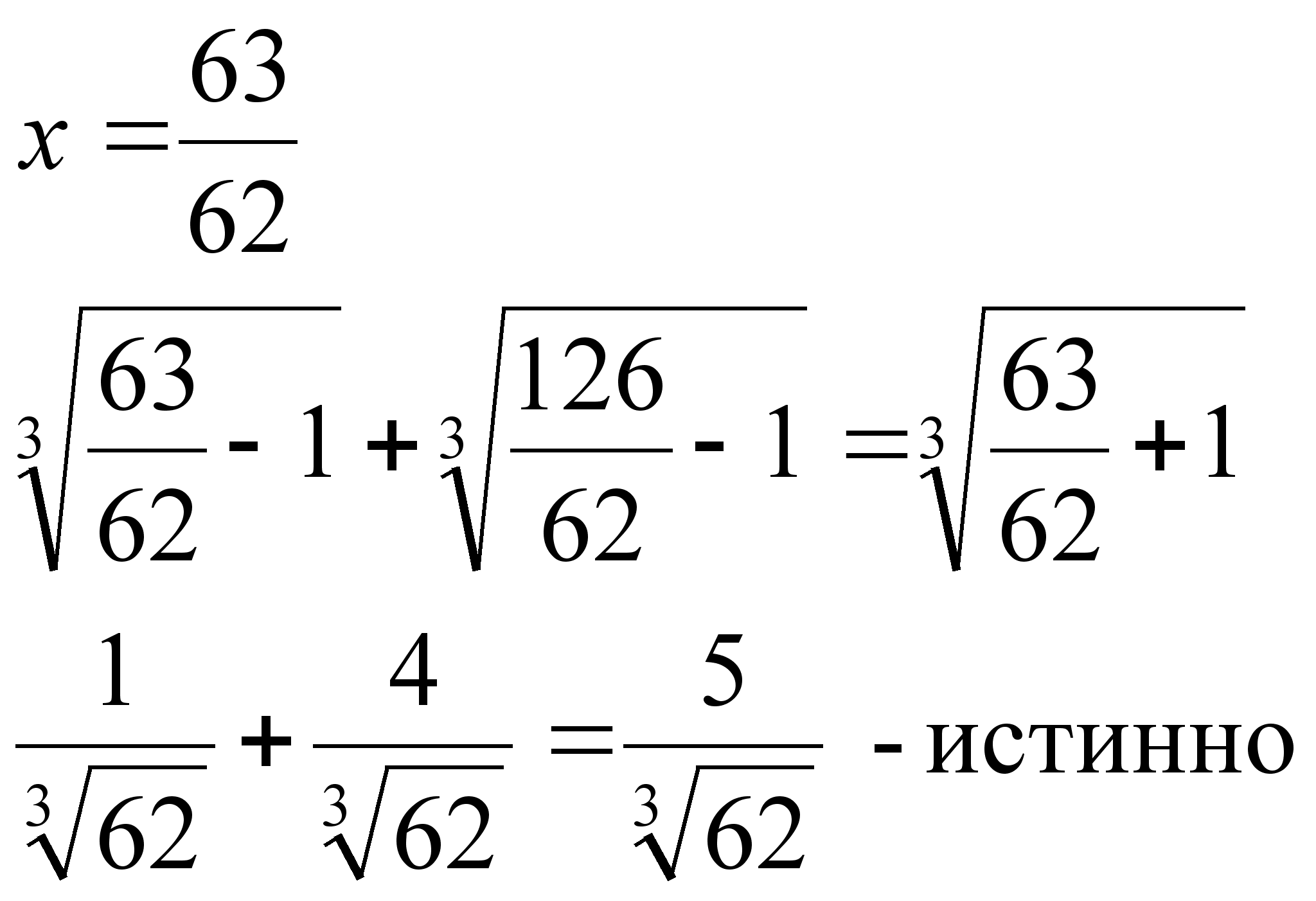
Ответ:
4)
решим соответствующее уравнение:
возводим в куб
делаем подстановку
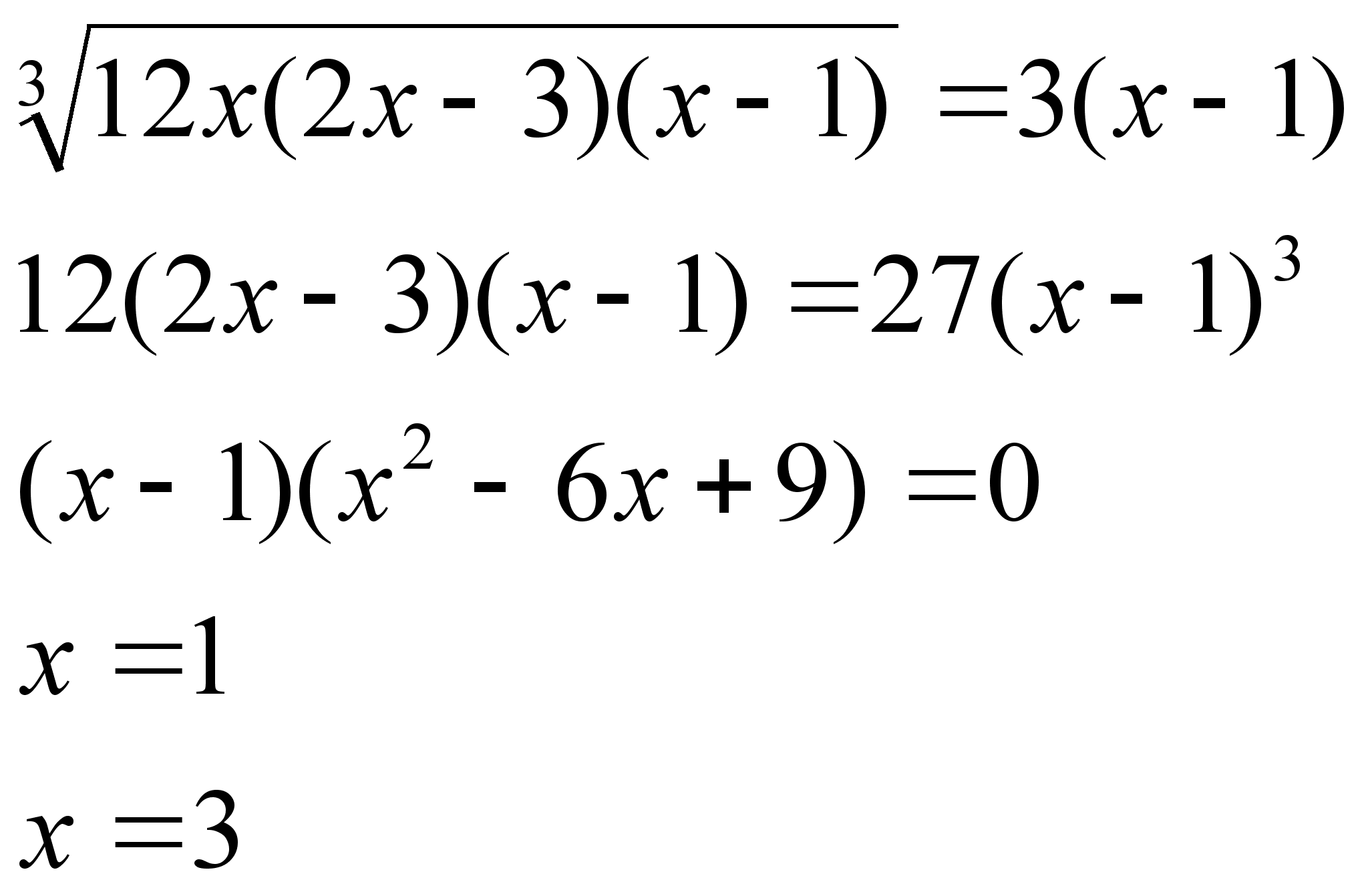
Проверка:
1. 
2.
+ - -
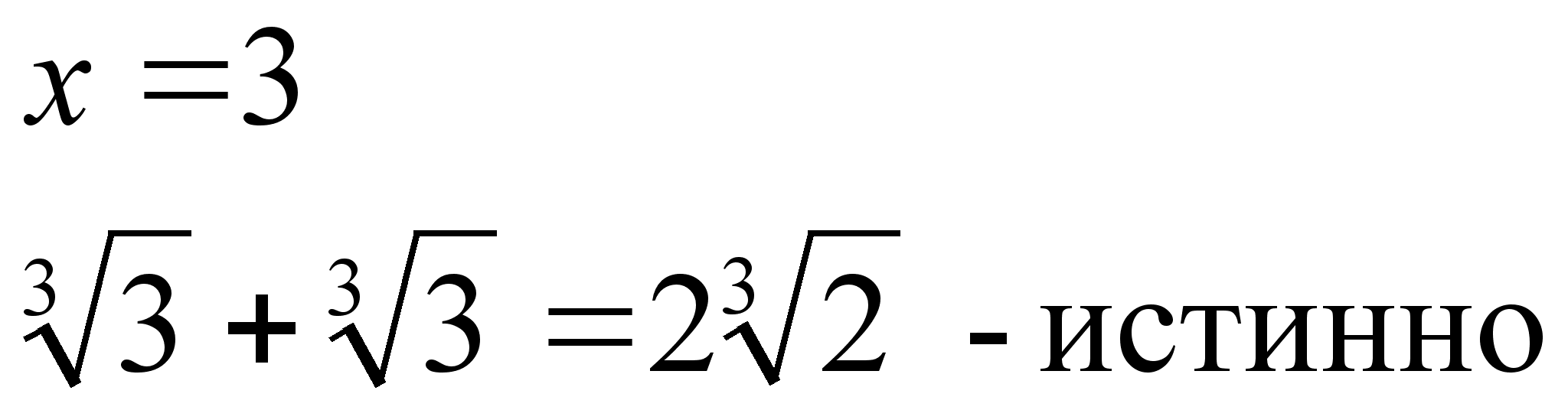
3
Ответ: 
5)
возводим в куб
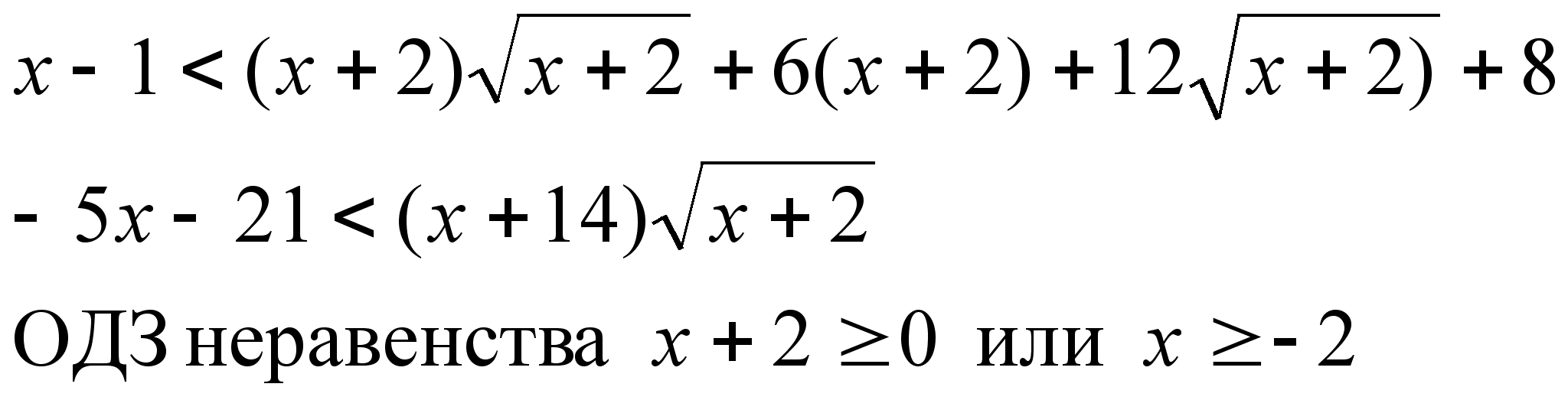
При
Значит последнее неравенство на ОДЗ всегда истинно.
Ответ:
6)
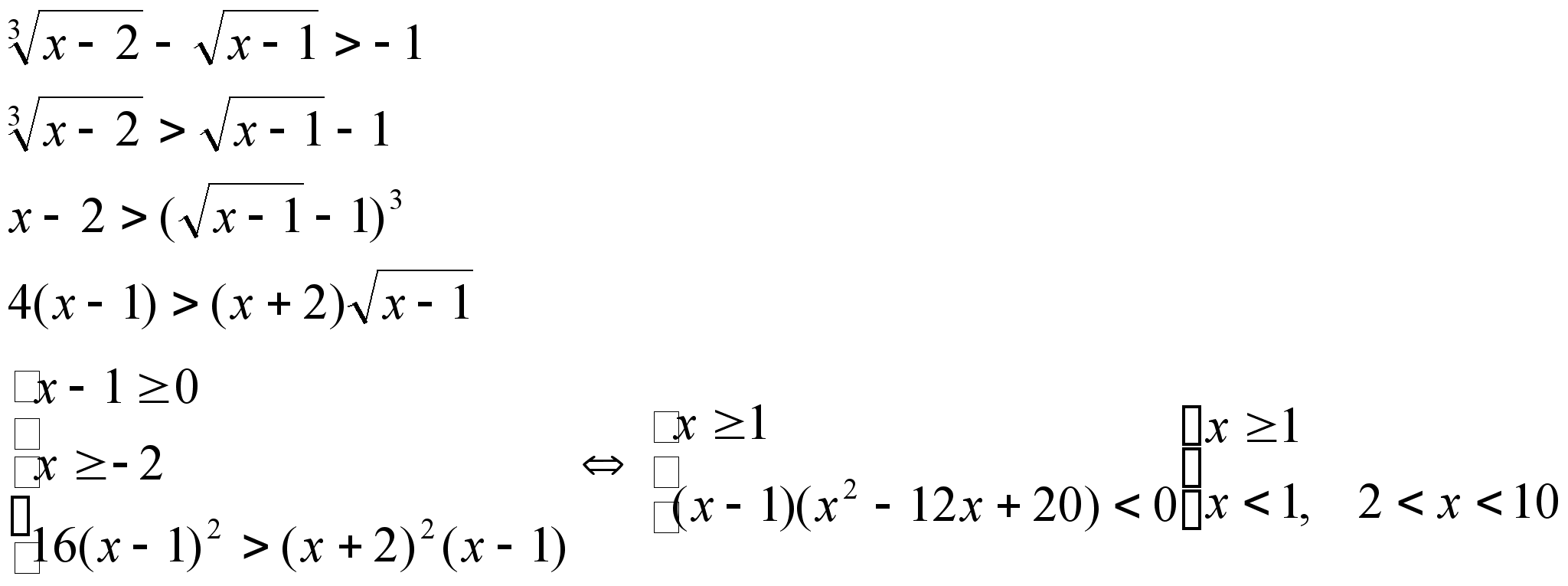
Ответ:
IV. Д/з
Похожие работы
... говоря о том, что некоторые виды технических средств обладают исключительно большими возможностями наглядного показа материала обучения. Олимпиада одна из основных форм организации внеклассной работы по математике. Термин «олимпиада» проявился давно, хотелось бы вспомнить об истории отечественной математической олимпиады. Сначала о ней говорили в единственном числе, поскольку она организовывалась ...
... и устойчивых требований, которые определяют характер и особенности организации коррекционно-образовательного процесса и управления познавательной деятельностью лиц с особыми образовательными потребностями. Специальная педагогика опирается на соответствующие обще- педагогические принципы организации образования и управления познавательной деятельностью, однако их реализация в системе специального ...
... труде - все это формирует и развивает познавательный интерес и превращает его в важный стимул учебной деятельности учащихся [20,46]. Существуют различные средства развития познавательного интереса: решение занимательных, логических задач, игра, исторические экскурсы и другие. Наиболее подробно остановимся на исторических экскурсах. Знакомство с историей науки полезно для каждого человека, а для ...
... учащихся к ЕГЭ, учителя математики СОШ №26 г.Якутска используют перечень вопросов содержания (кодификатор) школьного курса математики, усвоение которых проверяется при сдачи единого государственного экзамена 2007г. Элективный курс по подготовке к Единому Государственному Экзамену основан на повторении, систематизации и углублении знаний полученных ранее. Занятия проходят в форме свободного ...
0 комментариев