Навигация
Траектории автономных систем
1.2. Траектории автономных систем.
Будем рассматривать автономную систему в векторной форме:![]() (2)
(2)
где функция f(x) определена в ![]() .
.
Автономные системы обладают тем свойством, что если ![]() — решение уравнения (2), то
— решение уравнения (2), то ![]() ,
, ![]() , также решение уравнения (2). Отсюда в частности следует, что решение
, также решение уравнения (2). Отсюда в частности следует, что решение ![]() можно записать в виде
можно записать в виде ![]() . В геометрической интерпретации эта запись означает, что если две траектории уравнения (2) имеют общую точку, то они совпадают. При этом можно заметить, что траектория вполне определяется начальной точкой
. В геометрической интерпретации эта запись означает, что если две траектории уравнения (2) имеют общую точку, то они совпадают. При этом можно заметить, что траектория вполне определяется начальной точкой ![]() , поэтому можно везде считать
, поэтому можно везде считать ![]() .
.
Пусть ![]() — положение равновесия, т. е.
— положение равновесия, т. е. ![]() . Для того чтобы точка
. Для того чтобы точка ![]() была положением равновесия, необходимо и достаточно, чтобы
была положением равновесия, необходимо и достаточно, чтобы ![]() . Предположим теперь, что траектория решения
. Предположим теперь, что траектория решения ![]() не является положением равновесия, но имеет кратную точку, т. е. существуют
не является положением равновесия, но имеет кратную точку, т. е. существуют ![]() , такие, что
, такие, что ![]() . Так как
. Так как ![]() — не положение равновесия, то
— не положение равновесия, то ![]() . Поэтому можно считать, что
. Поэтому можно считать, что ![]() при
при ![]() . Обозначим
. Обозначим ![]() и покажем, что
и покажем, что ![]() — -периодическая функция.
— -периодическая функция.
Действительно, функция ![]() является решением уравнения (2) при
является решением уравнения (2) при ![]() , причем
, причем ![]() . В силу единственности
. В силу единственности ![]() и
и ![]() совпадают при всех
совпадают при всех ![]() . Применяя аналогичное рассуждение к решению
. Применяя аналогичное рассуждение к решению ![]() , получим, что
, получим, что ![]() определено при
определено при ![]() и функции
и функции ![]() и
и ![]() совпадают при этих t. Таким образом, можно продолжить
совпадают при этих t. Таким образом, можно продолжить ![]() на все
на все ![]() , при этом должно выполняться тождество
, при этом должно выполняться тождество
![]() ,
,
то есть ![]() — периодическая функция с наименьшим периодом.
— периодическая функция с наименьшим периодом.
Траектория такого решения является замкнутой кривой. Из приведенного вытекает следующий результат: Каждая траектория автономного уравнения (2) принадлежит одному из следующих трех типов:
положение равновесия;
замкнутая траектория, которой соответствует периодическое решение с положительным наименьшим периодом;
траектория без самопересечения, которой соответствует непериодическое решение.
1.3. Предельные множества траекторий.
Определение. Точка ![]() называется -предельной точкой траектории
называется -предельной точкой траектории ![]() ,
, ![]() , если существует последовательность
, если существует последовательность ![]() такая, что
такая, что ![]() при
при ![]() . Множество всех -предельных точек траектории называется ее -предельным множеством. Аналогично для траектории
. Множество всех -предельных точек траектории называется ее -предельным множеством. Аналогично для траектории ![]() при
при ![]() определяется понятие -предельной точки как предела
определяется понятие -предельной точки как предела ![]() , а также -предельного множества.
, а также -предельного множества.
Определение. Траектория ![]() называется положительно (отрицательно) устойчивой по Лагранжу (обозн.
называется положительно (отрицательно) устойчивой по Лагранжу (обозн. ![]() (
(![]() )), если существует компакт
)), если существует компакт ![]() такой, что
такой, что ![]() при всех
при всех ![]() (
(![]() ), при которых
), при которых ![]() определена. Иными словами, если траектория всегда остается в некоторой ограниченной области фазового пространства.
определена. Иными словами, если траектория всегда остается в некоторой ограниченной области фазового пространства.
Можно показать, что предельное множество устойчивой по Лагранжу траектории не пусто, компактно и связно.
Траектория ![]() называется устойчивой по Пуассону, если каждая ее точка является -предельной и -предельной, т. е.
называется устойчивой по Пуассону, если каждая ее точка является -предельной и -предельной, т. е. ![]() . Примером устойчивой по Пуассону траектории является состояние равновесия. Если же рассматривается траектория, отличная от неподвижной точки, то устойчивой по Пуассону она будет в том случае, если обладает свойством возвращаться в сколь угодно малую окрестность каждой своей точки бесконечное число раз. Поэтому устойчивыми по Пуассону будут циклы и квазипериодические траектории (суперпозиция двух периодических колебаний с несоизмеримыми частотами), а также более сложные траектории, возникающие в хаотических системах.
. Примером устойчивой по Пуассону траектории является состояние равновесия. Если же рассматривается траектория, отличная от неподвижной точки, то устойчивой по Пуассону она будет в том случае, если обладает свойством возвращаться в сколь угодно малую окрестность каждой своей точки бесконечное число раз. Поэтому устойчивыми по Пуассону будут циклы и квазипериодические траектории (суперпозиция двух периодических колебаний с несоизмеримыми частотами), а также более сложные траектории, возникающие в хаотических системах.
Рассмотрим (без доказательств) некоторые свойства предельных множеств в случае n = 2.
Похожие работы
... пакетах. Заключение Результатом выполнения курсового проекта является готовый программный продукт, позволяющий решать задачу Коши для системы дифференциальных уравнений при помощи неявной схемы Адамса 3-го порядка, демонстрирующий возможности численного решения поставленной задачи с заданной степенью точности. Готовый программный продукт может найти широкое применение при решении многих ...
... в векторно-матричной форме записи имеет следующий вид: . В таблице приведены результаты вычисления переходных процессов для векторно-матричного неоднородного дифференциального уравнения по формуле аналитического решения и трем рекуррентным выражениям, использующим различные квадратурные формулы интегрирования. Для заполнения таблицы с шагом 0.1 по третьей рекуррентной формуле второе ...
... при финансовой поддержке государственной научно-технической программы «Физика квантовых и волновых процессов» (проект 1.61) и физического учебно-научного центра «Фундаментальная оптика и спектроскопия». 1. Асимптотическое поведение решений дифференциальных уравнений с малым параметром Многие колебательные системы описываются дифференциальными уравнениями с малым параметром при производных: ...
... была построена теория вложения функциональных пространств, которые в настоящее время носят название пространств Соболева. А.Н. Тихоновым была построена теория некорректных задач. Выдающийся вклад в современную теорию дифференциальных уравнений внесли российские математики Н.Н. Боголюбов, А.Н. Колмогоров, И.Г. Петровский, Л.С. Понтрягин, С.Л. Соболев, А.Н. Тихонов и другие. Влияние на развитие ...
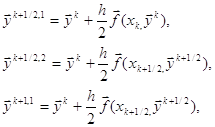
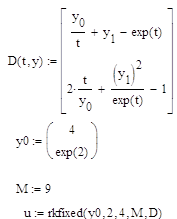
0 комментариев