Линейные однородные системы с периодическими коэффициентами

1.5. Линейные однородные системы с периодическими коэффициентами.

В данном пункте излагается так называемая теория Флоке.

Будем рассматривать систему вида (4)

где , а матричная функция P(t) удовлетворяет условию P(t + ) = P(t), >0 при всех . Такие матричные функции будем называть периодическими с периодом  или -периодическими.

Теорема Флоке. Фундаментальная матрица системы (4) имеет вид

где G — -периодическая матрица, R — постоянная матрица.

Матрица В, определяемая равенством , называется матрицей монодромии. Для нее справедливо . Она определяется с помощью фундаментальной матрицы неоднозначно, но можно показать, что все матрицы монодромии подобны. Часто матрицей монодромии называют ту, которая порождается нормированной при  фундаментальной матрицей , то есть .

Собственные числа  матрицы монодромии называются мультипликаторами уравнения (4), а собственные числа  матрицы R — характеристическими показателями. Из определения R имеем , при этом простым мультипликаторам соответствуют простые характеристические показатели, а кратным — характеристические показатели с элементарными делителями той же кратности.

Характеристические показатели определены с точностью до . Из  и формулы Лиувилля следует, что .

Название мультипликатор объясняется следующей теоремой:

Теорема. Число  является мультипликатором уравнения (4) тогда и только тогда, когда существует ненулевое решение  этого уравнения такое, что при всех t .

Следствие 1. Линейная периодическая система (4) имеет нетривиальное решение периода  тогда и только тогда, когда по меньшей мере один из ее мультипликаторов равен единице.

Следствие 2. Мультипликатору  соответствует так называемое антипериодическое решение  периода , т. е. . Отсюда имеем:

Таким образом,  есть периодическое решение с периодом . Аналогично, если  (p и q — целые, ), то периодическая система имеет периодическое решение с периодом .

Пусть , где  — матрица из теоремы Флоке,  — ее жорданова форма. По теореме Флоке , или , (5)

где  — фундаментальная матрица,  — -периодическая матрица. В структуре фундаментальной матрицы линейной системы с периодическими коэффициентами характеристические показатели играют ту же роль, что и собственные числа матрицы коэффициентов в структуре фундаментальной матрицы линейной системы с постоянными коэффициентами.

Пример. Рассмотрим дифференциальное уравнение второго порядка

, (6)

где  — -периодическая вещественная скалярная функция. Мультипликаторами уравнения (6) будем называть мультипликаторы соответствующей линейной системы, т. е. системы

с матрицей . Так как , то . Мультипликаторы являются собственными числами матрицы

,

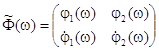где  — решение уравнения (6), удовлетворяющее начальным условиям  , а  — решение уравнения (6), удовлетворяющее начальным условиям  . Пусть  — характеристическое уравнение для определения мультипликаторов. Так как , то оно принимает вид , где .

Похожие работы

Решение систем дифференциальных уравнений при помощи неявной схемы Адамса 3-го порядка

Скачать

39446

2

12

... пакетах.   Заключение   Результатом выполнения курсового проекта является готовый программный продукт, позволяющий решать задачу Коши для системы дифференциальных уравнений при помощи неявной схемы Адамса 3-го порядка, демонстрирующий возможности численного решения поставленной задачи с заданной степенью точности. Готовый программный продукт может найти широкое применение при решении многих ...

Решение систем дифференциальных уравнений

Скачать

10895

2

6

... в векторно-матричной форме записи имеет следующий вид: . В таблице приведены результаты вычисления переходных процессов для векторно-матричного неоднородного дифференциального уравнения по формуле аналитического решения и трем рекуррентным выражениям, использующим различные квадратурные формулы интегрирования. Для заполнения таблицы с шагом 0.1 по третьей рекуррентной формуле второе ...

Асимптотика решений дифференциальных уравнений

Скачать

31319

15

25

... при финансовой поддержке государственной научно-технической программы «Физика квантовых и волновых процессов» (проект 1.61) и физического учебно-научного центра «Фундаментальная оптика и спектроскопия». 1. Асимптотическое поведение решений дифференциальных уравнений с малым параметром Многие колебательные системы описываются дифференциальными уравнениями с малым параметром при производных: ...

Роль теории дифференциальных уравнений в современной математике и ее приложениях

Скачать

32343

0

0

... была построена теория вложения функциональных пространств, которые в настоящее время носят название пространств Соболева. А.Н. Тихоновым была построена теория некорректных задач. Выдающийся вклад в современную теорию дифференциальных уравнений внесли российские математики Н.Н. Боголюбов, А.Н. Колмогоров, И.Г. Петровский, Л.С. Понтрягин, С.Л. Соболев, А.Н. Тихонов и другие. Влияние на развитие ...