Навигация
Устойчивость по первому приближению
2.6. Устойчивость по первому приближению.
Вернемся к рассмотрению уравнения (1), где ![]() . После замены
. После замены ![]() получим уравнение (2), которое, используя разложение в ряд Тейлора, запишем в виде
получим уравнение (2), которое, используя разложение в ряд Тейлора, запишем в виде
![]() , (8)
, (8)
где ![]() при
при ![]() . (9)
. (9)
Теорема 5. Пусть ![]() — постоянная матрица, предельный переход в (9) выполняется равномерно по
— постоянная матрица, предельный переход в (9) выполняется равномерно по ![]() и вещественные части собственных чисел матрицы
и вещественные части собственных чисел матрицы ![]() отрицательны. Тогда решение
отрицательны. Тогда решение ![]() уравнения (8) асимптотически устойчиво.
уравнения (8) асимптотически устойчиво.
Теорема 6. Пусть ![]() — постоянная матрица, предельный переход в (9) выполняется равномерно по
— постоянная матрица, предельный переход в (9) выполняется равномерно по ![]() . Для устойчивости по Ляпунову нулевого решения уравнения (8) необходимо, чтобы вещественные части собственных чисел матрицы
. Для устойчивости по Ляпунову нулевого решения уравнения (8) необходимо, чтобы вещественные части собственных чисел матрицы ![]() были неположительны.
были неположительны.
Рассмотрим теперь автономное уравнение (1): ![]() , (10)
, (10)
где функция ![]() непрерывно дифференцируема при
непрерывно дифференцируема при ![]() , причем
, причем ![]() . Тогда
. Тогда ![]() является положением равновесия уравнения (10). После замены
является положением равновесия уравнения (10). После замены ![]() уравнение (10) принимает вид
уравнение (10) принимает вид ![]() , где
, где ![]() , функция
, функция ![]() непрерывно дифференцируема при
непрерывно дифференцируема при ![]() и
и
![]() при
при ![]() . (11)
. (11)
Из (11) и теорем 5 и 6 вытекает следующее утверждение.
Теорема 7. Если все собственные числа матрицы ![]() имеют отрицательные вещественные части, то положение равновесия
имеют отрицательные вещественные части, то положение равновесия ![]() асимптотически устойчиво; если же хоть одно из собственных чисел имеет положительную вещественную часть, то оно неустойчиво.
асимптотически устойчиво; если же хоть одно из собственных чисел имеет положительную вещественную часть, то оно неустойчиво.
Пример. Рассмотрим систему двух уравнений ![]() Координаты положений равновесия определяются из уравнений
Координаты положений равновесия определяются из уравнений ![]() . Положения равновесия:
. Положения равновесия:
![]()
Соответствующие матрицы ![]() имеют вид
имеют вид
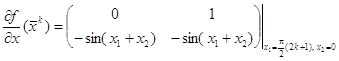 , или
, или ![]() .
.
Собственные числа определяются уравнением ![]() . При k четном
. При k четном ![]() , при k нечетном
, при k нечетном ![]() . По теореме 7 при k четном решения
. По теореме 7 при k четном решения ![]() асимптотически устойчивы, а при k нечетном неустойчивы.
асимптотически устойчивы, а при k нечетном неустойчивы.
Предположим теперь, что правая часть уравнения (1) и решение ![]() периодичны по t с одним и тем же периодом . Тогда в уравнении (8)
периодичны по t с одним и тем же периодом . Тогда в уравнении (8) ![]() ,
, ![]() . Далее, так как
. Далее, так как ![]() равномерно непрерывна на компакте
равномерно непрерывна на компакте ![]() , то в силу периодичности
, то в силу периодичности ![]()
![]() выполняется равномерно по
выполняется равномерно по ![]() . Поскольку
. Поскольку ![]() — периодическая матрица, то существует замена переменных
— периодическая матрица, то существует замена переменных ![]() , (12)
, (12)
где ![]() — периодическая с периодом функция класса
— периодическая с периодом функция класса ![]() , причем
, причем ![]() , переводящая уравнение
, переводящая уравнение ![]() в
в ![]() с постоянной матрицей коэффициентов
с постоянной матрицей коэффициентов ![]() , определяемой теоремой Флоке. Следовательно, замена (12) переводит (8) в уравнение
, определяемой теоремой Флоке. Следовательно, замена (12) переводит (8) в уравнение
![]() , (13)
, (13)
причем функция ![]() определена и непрерывна в области вида
определена и непрерывна в области вида ![]() . Условие (9) также выполняется. Действительно,
. Условие (9) также выполняется. Действительно, 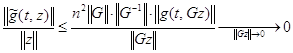 в силу (9), ограниченности
в силу (9), ограниченности ![]() и
и ![]() и поскольку
и поскольку ![]() эквивалентно
эквивалентно ![]() . При этом, как отмечалось, имеет место равномерность по t.
. При этом, как отмечалось, имеет место равномерность по t.
Согласно лемме из п. 2.1. вопрос об устойчивости тривиального решения уравнения (8) эквивалентен вопросу об устойчивости тривиального решения уравнения (13). Так как ![]() , где
, где ![]() — собственные числа матрицы
— собственные числа матрицы ![]() , а
, а ![]() — мультипликаторы линейного уравнения
— мультипликаторы линейного уравнения ![]() , называемые также мультипликаторами периодического решения
, называемые также мультипликаторами периодического решения ![]() , то из теорем 5 и 6 вытекает следующая теорема:
, то из теорем 5 и 6 вытекает следующая теорема:
Теорема 8. Если модули всех мультипликаторов периодического решения периодического уравнения (1) меньше единицы, то это решение асимптотически устойчиво. Если же модуль хоть одного из мультипликаторов больше единицы, то оно неустойчиво.
Рассмотрим смешанный случай, когда исследуется устойчивость -периодического решения ![]() автономного уравнения (10). Дифференцируя тождество
автономного уравнения (10). Дифференцируя тождество ![]() , получаем
, получаем ![]() . Следовательно, функция
. Следовательно, функция ![]() является -периодическим решением уравнения в вариациях
является -периодическим решением уравнения в вариациях ![]() . По следствию 1 п. 1.5. один из мультипликаторов равен единице. Если среди остальных мультипликаторов имеются такие, модули которых больше единицы, то решение
. По следствию 1 п. 1.5. один из мультипликаторов равен единице. Если среди остальных мультипликаторов имеются такие, модули которых больше единицы, то решение ![]() неустойчиво по теореме 8. В противном случае теорема 8 неприменима.
неустойчиво по теореме 8. В противном случае теорема 8 неприменима.
Теорема 9. (Андронова-Витта) Если ![]() мультипликаторов периодического решения уравнения (10) имеют модули, меньшие единицы, то это решение устойчиво по Ляпунову.
мультипликаторов периодического решения уравнения (10) имеют модули, меньшие единицы, то это решение устойчиво по Ляпунову.
Замечание. Уравнение (10) автономно, поэтому наряду с решением ![]() имеются и решения
имеются и решения ![]() ,
, ![]() , следовательно, решение
, следовательно, решение ![]() не может быть асимптотически устойчивым.
не может быть асимптотически устойчивым.
Похожие работы
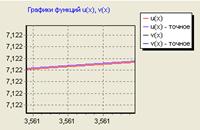
... пакетах. Заключение Результатом выполнения курсового проекта является готовый программный продукт, позволяющий решать задачу Коши для системы дифференциальных уравнений при помощи неявной схемы Адамса 3-го порядка, демонстрирующий возможности численного решения поставленной задачи с заданной степенью точности. Готовый программный продукт может найти широкое применение при решении многих ...
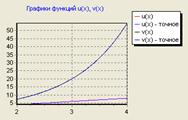
... в векторно-матричной форме записи имеет следующий вид: . В таблице приведены результаты вычисления переходных процессов для векторно-матричного неоднородного дифференциального уравнения по формуле аналитического решения и трем рекуррентным выражениям, использующим различные квадратурные формулы интегрирования. Для заполнения таблицы с шагом 0.1 по третьей рекуррентной формуле второе ...
... при финансовой поддержке государственной научно-технической программы «Физика квантовых и волновых процессов» (проект 1.61) и физического учебно-научного центра «Фундаментальная оптика и спектроскопия». 1. Асимптотическое поведение решений дифференциальных уравнений с малым параметром Многие колебательные системы описываются дифференциальными уравнениями с малым параметром при производных: ...
... была построена теория вложения функциональных пространств, которые в настоящее время носят название пространств Соболева. А.Н. Тихоновым была построена теория некорректных задач. Выдающийся вклад в современную теорию дифференциальных уравнений внесли российские математики Н.Н. Боголюбов, А.Н. Колмогоров, И.Г. Петровский, Л.С. Понтрягин, С.Л. Соболев, А.Н. Тихонов и другие. Влияние на развитие ...
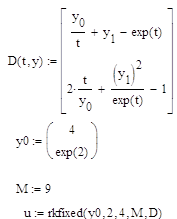
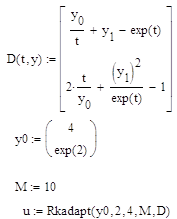
0 комментариев