Навигация
Устойчивость периодических решений
2.3. Устойчивость периодических решений.
Рассмотрим уравнение (3) с периодическими коэффициентами, т. е. ![]() , (4)
, (4)
где ![]() . По формуле (5) предыдущей главы уравнение (4) имеет в рассматриваемом случае фундаментальную матрицу
. По формуле (5) предыдущей главы уравнение (4) имеет в рассматриваемом случае фундаментальную матрицу ![]() , где
, где ![]() — неособая -периодическая непрерывная матрица, тем самым ограниченная вместе с обратной,
— неособая -периодическая непрерывная матрица, тем самым ограниченная вместе с обратной, ![]() — жорданова матрица, собственные числа
— жорданова матрица, собственные числа ![]() которой — характеристические показатели уравнения (4). Из леммы 1 следует, что характеристические показатели играют при оценке фундаментальной матрицы ту же роль, что собственные числа
которой — характеристические показатели уравнения (4). Из леммы 1 следует, что характеристические показатели играют при оценке фундаментальной матрицы ту же роль, что собственные числа ![]() , когда
, когда ![]() постоянна. Учитывая, что
постоянна. Учитывая, что ![]() , где
, где ![]() — мультипликаторы уравнения, получаем следующий результат:
— мультипликаторы уравнения, получаем следующий результат:
Теорема 3. Линейная однородная система с периодическими коэффициентами: 1) устойчива по Ляпунову тогда и только тогда, когда все ее мультипликаторы не превышают по модулю единицы, а равные единице по модулю либо простые, либо им соответствуют простые элементарные делители матрицы монодромии; 2) асимптотически устойчива тогда и только тогда, когда модули всех мультипликаторов меньше единицы.
Пример. Рассмотрим уравнение из примера п. 1.5:
![]()
Уравнение будем называть устойчивым по Ляпунову, асимптотически устойчивым или неустойчивым, если таковой является соответствующая ему линейная система. Мультипликаторы находятся из уравнения ![]() :
: ![]() , где
, где ![]() . Поэтому можно сделать вывод, что при
. Поэтому можно сделать вывод, что при ![]() оба мультипликатора вещественны и один из них по абсолютной величине больше единицы, а при
оба мультипликатора вещественны и один из них по абсолютной величине больше единицы, а при ![]() мультипликаторы являются комплексно-сопряженными с модулями, равными единице. По теореме 3 при
мультипликаторы являются комплексно-сопряженными с модулями, равными единице. По теореме 3 при ![]() уравнение
уравнение ![]() неустойчиво, а при
неустойчиво, а при ![]() оно устойчиво по Ляпунову, но не асимптотически.
оно устойчиво по Ляпунову, но не асимптотически.
2.4. Классификация положений равновесия системы второго порядка.
Исследуем на устойчивость положения равновесия линейной однородной системы двух уравнений с постоянными коэффициентами. Пусть ![]() , где
, где ![]() . Как было показано в пункте 1.4, тип особой точки такой системы определяется корнями характеристического уравнения
. Как было показано в пункте 1.4, тип особой точки такой системы определяется корнями характеристического уравнения ![]() или
или ![]() . Его корни можно найти по формуле
. Его корни можно найти по формуле
![]() .
.
Рассмотрим следующие случаи согласно пункту 1.4.
1) ![]() вещественны, различны и
вещественны, различны и ![]() (
(![]() ). Параметрические уравнения траекторий:
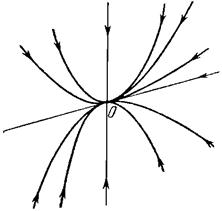
). Параметрические уравнения траекторий: ![]() . Положение равновесия называется узел. Если корни
. Положение равновесия называется узел. Если корни ![]() положительны (
положительны (![]() ), то решения будут неограниченно возрастать, и особая точка — неустойчивый узел.
), то решения будут неограниченно возрастать, и особая точка — неустойчивый узел.
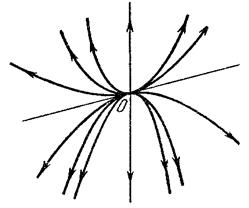
Если ![]() отрицательны (
отрицательны (![]() ), то решения с ростом времени будут неограниченно уменьшаться, то есть положение равновесия будет асимптотически устойчивым. Особая точка — устойчивый узел.
), то решения с ростом времени будут неограниченно уменьшаться, то есть положение равновесия будет асимптотически устойчивым. Особая точка — устойчивый узел.
2) ![]() вещественны и
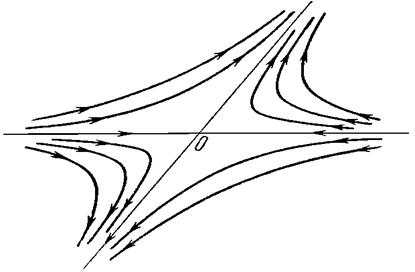
вещественны и ![]() (
(![]() ). В этом случае одна из траекторий всегда будет неограниченно возрастать, а другая неограниченно уменьшаться. Таким образом, седло всегда неустойчиво.
). В этом случае одна из траекторий всегда будет неограниченно возрастать, а другая неограниченно уменьшаться. Таким образом, седло всегда неустойчиво.
3) ![]() комплексно-сопряженные, но не чисто мнимые (
комплексно-сопряженные, но не чисто мнимые (![]() ). Решение в полярных координатах запишется в виде
). Решение в полярных координатах запишется в виде ![]() , где
, где ![]() . Если
. Если ![]() (
(![]() ), то спирали будут раскручиваться от особой точки, и фокус будет неустойчивым.
), то спирали будут раскручиваться от особой точки, и фокус будет неустойчивым.
Если ![]() (
(![]() ), то особая точка — устойчивый фокус, причем устойчивость асимптотическая.
), то особая точка — устойчивый фокус, причем устойчивость асимптотическая.


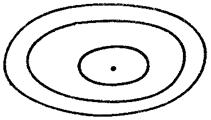
4) ![]() (
(![]() ). Особая точка — центр, траектории — окружности, то есть положение равновесия является устойчивым, но не асимптотически.
). Особая точка — центр, траектории — окружности, то есть положение равновесия является устойчивым, но не асимптотически.
5) ![]() . Если
. Если ![]() , то получаем неустойчивый узел, либо вырожденный, либо дикритический. Если
, то получаем неустойчивый узел, либо вырожденный, либо дикритический. Если ![]() , положение равновесия будет асимптотически устойчивым.
, положение равновесия будет асимптотически устойчивым.

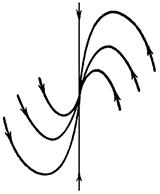
6) Один из корней равен нулю (например ![]() ). Траекториями являются прямые, параллельные друг другу. Если
). Траекториями являются прямые, параллельные друг другу. Если ![]() , то получаем прямую неустойчивых особых точек. Если
, то получаем прямую неустойчивых особых точек. Если ![]() , то прямая будет содержать устойчивые особые точки.
, то прямая будет содержать устойчивые особые точки.
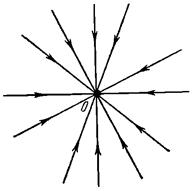
7) Оба корня равны нулю. Тогда ![]() . Особая точка неустойчива.
. Особая точка неустойчива.
Пример. Рассмотрим систему ![]() . Положение равновесия находится из уравнения
. Положение равновесия находится из уравнения ![]() , или
, или ![]() , откуда
, откуда ![]() . Следовательно, положение равновесия — неустойчивый узел. Жорданова форма матрицы А имеет вид:
. Следовательно, положение равновесия — неустойчивый узел. Жорданова форма матрицы А имеет вид:
![]() .
.
Найдем координаты преобразования ![]() , приводящего матрицу А к жордановой форме, то есть переводящего систему к виду
, приводящего матрицу А к жордановой форме, то есть переводящего систему к виду ![]() . Дифференцируя эти уравнения и подставляя в исходную систему, получаем:
. Дифференцируя эти уравнения и подставляя в исходную систему, получаем:
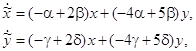
откуда с учетом ![]()
![]() , — произвольное,
, — произвольное, ![]() , — произвольное. Получаем преобразование
, — произвольное. Получаем преобразование ![]() . Определим новое положение осей:
. Определим новое положение осей:
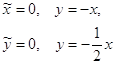
Решение системы ![]() запишется в виде
запишется в виде ![]() , а исходной системы отсюда
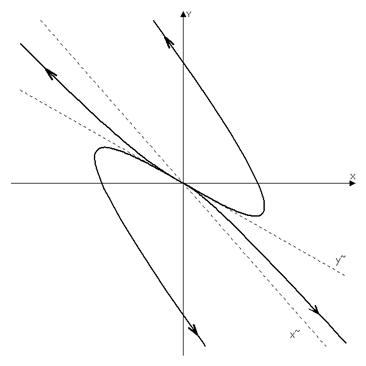
, а исходной системы отсюда 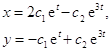 . Схематическое изображение траекторий:
. Схематическое изображение траекторий:
Рассмотрим теперь некоторые положения равновесия в трехмерном пространстве. Характеристическое уравнение — кубическое с вещественными коэффициентами, оно может иметь три вещественных или один вещественный и два комплексно-сопряженных корня. В зависимости от расположения этих корней ![]() на плоскости
на плоскости ![]() возможно 10 "грубых" случаев (рис. 3, 1)-5) и 1')-5')) и ряд "вырожденных" (рис. 3, 6)-9)), когда вещественная часть одного из корней равна нулю или вещественной части не сопряженного с ним корня. Случаи кратных корней здесь не рассматриваются.
возможно 10 "грубых" случаев (рис. 3, 1)-5) и 1')-5')) и ряд "вырожденных" (рис. 3, 6)-9)), когда вещественная часть одного из корней равна нулю или вещественной части не сопряженного с ним корня. Случаи кратных корней здесь не рассматриваются.
Поведение фазовых траекторий в приведенных случаях показано на рис. 4. Случаи 1')-5') получаются из случаев 1)-5) изменением направления оси t, так что на рис. 4 надо лишь заменить все стрелки на противоположные.
Устойчивость по Ляпунову в рассмотренных случаях следующая. Все случаи 1')-5'), а также 2), 5), 8) и 9) неустойчивы. Случаи 1), 3) и 4) устойчивы асимптотически. Случай 6) устойчив.
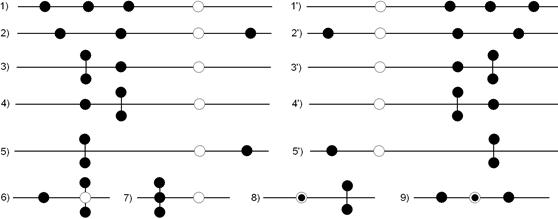
Рис. 3. Собственные числа матрицы А. Закрашенным кружком отмечены ![]() ,
,
светлым — начало координат.
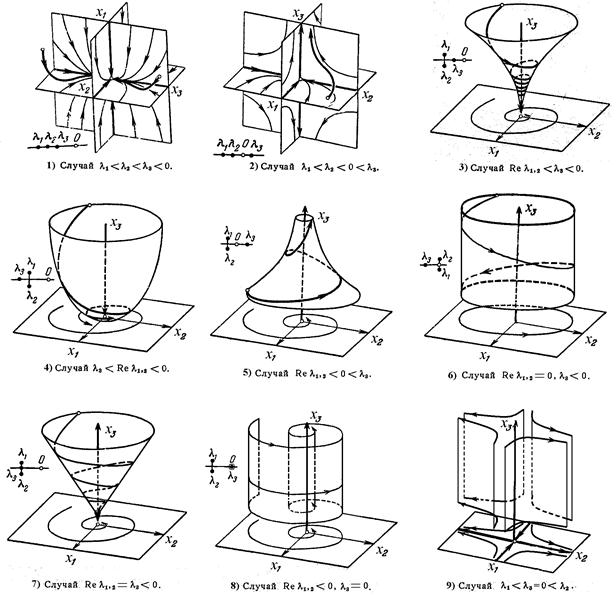
Рис. 4. Фазовые кривые в трехмерном пространстве.
Похожие работы
... пакетах. Заключение Результатом выполнения курсового проекта является готовый программный продукт, позволяющий решать задачу Коши для системы дифференциальных уравнений при помощи неявной схемы Адамса 3-го порядка, демонстрирующий возможности численного решения поставленной задачи с заданной степенью точности. Готовый программный продукт может найти широкое применение при решении многих ...
... в векторно-матричной форме записи имеет следующий вид: . В таблице приведены результаты вычисления переходных процессов для векторно-матричного неоднородного дифференциального уравнения по формуле аналитического решения и трем рекуррентным выражениям, использующим различные квадратурные формулы интегрирования. Для заполнения таблицы с шагом 0.1 по третьей рекуррентной формуле второе ...
... при финансовой поддержке государственной научно-технической программы «Физика квантовых и волновых процессов» (проект 1.61) и физического учебно-научного центра «Фундаментальная оптика и спектроскопия». 1. Асимптотическое поведение решений дифференциальных уравнений с малым параметром Многие колебательные системы описываются дифференциальными уравнениями с малым параметром при производных: ...
... была построена теория вложения функциональных пространств, которые в настоящее время носят название пространств Соболева. А.Н. Тихоновым была построена теория некорректных задач. Выдающийся вклад в современную теорию дифференциальных уравнений внесли российские математики Н.Н. Боголюбов, А.Н. Колмогоров, И.Г. Петровский, Л.С. Понтрягин, С.Л. Соболев, А.Н. Тихонов и другие. Влияние на развитие ...
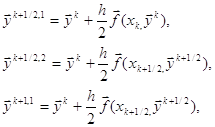
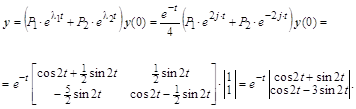
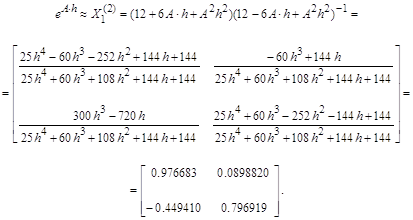
0 комментариев