Навигация
Автономные системы на плоскости. Предельные циклы
2.5. Автономные системы на плоскости. Предельные циклы.
Рассмотрим автономную двумерную систему
![]() , (5)
, (5)
где ![]() — область.
— область.
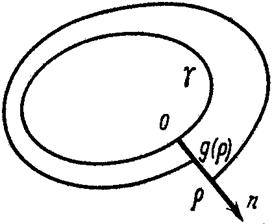
Предположим, что система (5) имеет замкнутую траекторию ![]() с наименьшим периодом
с наименьшим периодом ![]() . Возьмем произвольную точку
. Возьмем произвольную точку ![]() и проведем через нее нормаль
и проведем через нее нормаль ![]() к
к ![]() единичной длины. Для определенности считаем, что
единичной длины. Для определенности считаем, что ![]() направлен во внешнюю область. Не нарушая общности, считаем также, что
направлен во внешнюю область. Не нарушая общности, считаем также, что ![]() — начало координат (этого можно добиться заменой
— начало координат (этого можно добиться заменой ![]() ). Точки на нормали
). Точки на нормали ![]() определяются единственной координатой
определяются единственной координатой ![]() . В качестве
. В качестве ![]() берем расстояние от точки нормали до начала координат, если точка лежит снаружи
берем расстояние от точки нормали до начала координат, если точка лежит снаружи ![]() , и это расстояние, взятое с обратным знаком, если она лежит внутри
, и это расстояние, взятое с обратным знаком, если она лежит внутри ![]() .
.
Рассмотрим траектории ![]() , проходящие через точки нормали. Запишем уравнение
, проходящие через точки нормали. Запишем уравнение
![]() (6)
(6)
с неизвестными t, s ( — параметр).
Лемма 3. Существует ![]() такое, что в области
такое, что в области ![]() уравнение (6) имеет единственное решение
уравнение (6) имеет единственное решение ![]() , удовлетворяющее условиям
, удовлетворяющее условиям ![]() , причем функции
, причем функции ![]() непрерывно дифференцируемы при
непрерывно дифференцируемы при ![]() .
.
Доказательство. Так как ![]() — решение с периодом , то по теореме о дифференцируемости решения функция
— решение с периодом , то по теореме о дифференцируемости решения функция ![]() определена и непрерывно дифференцируема по t и в некоторой окрестности точки
определена и непрерывно дифференцируема по t и в некоторой окрестности точки ![]() . Тогда функция
. Тогда функция ![]() определена и непрерывно дифференцируема в некоторой окрестности точки
определена и непрерывно дифференцируема в некоторой окрестности точки ![]() . Так как
. Так как ![]() ‑периодична, то
‑периодична, то ![]() . Рассмотрим якобиан
. Рассмотрим якобиан ![]() в точке
в точке ![]() . Имеем
. Имеем ![]() . Следовательно, в точке
. Следовательно, в точке ![]()
![]() , поскольку
, поскольку ![]() и
и ![]() — ортогональные векторы. Тогда утверждение леммы вытекает из теоремы о неявной функции.
— ортогональные векторы. Тогда утверждение леммы вытекает из теоремы о неявной функции.
Следствие. Справедлива формула
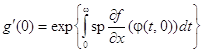 .
.
Выясним геометрический смысл функций ![]() . Лемма 3 утверждает, что каждая траектория, пересекающая нормаль
. Лемма 3 утверждает, что каждая траектория, пересекающая нормаль ![]() в точке
в точке ![]() из -окрестности начала координат, вновь пересечет ее через промежуток времени
из -окрестности начала координат, вновь пересечет ее через промежуток времени ![]() в точке
в точке ![]() . При этом так как функция
. При этом так как функция ![]() также делает полный оборот вдоль
также делает полный оборот вдоль ![]() при
при ![]() , то траектория
, то траектория ![]() также делает полный оборот при
также делает полный оборот при ![]() , оставаясь в малой окрестности
, оставаясь в малой окрестности ![]() , если достаточно мало.
, если достаточно мало.
Функция ![]() называется функцией последования.
называется функцией последования.
Определение. Замкнутая траектория ![]() автономного уравнения (5) называется устойчивым предельным циклом, если существует такое
автономного уравнения (5) называется устойчивым предельным циклом, если существует такое ![]() , что
, что ![]() является -предельным множеством для любой траектории, проходящей через точку из -окрестности кривой
является -предельным множеством для любой траектории, проходящей через точку из -окрестности кривой ![]() .
.
Определение. Замкнутая траектория ![]() автономного уравнения (5) называется неустойчивым предельным циклом, если существует такое
автономного уравнения (5) называется неустойчивым предельным циклом, если существует такое ![]() , что
, что ![]() является -предельным множеством для любой траектории, проходящей через точку из -окрестности кривой
является -предельным множеством для любой траектории, проходящей через точку из -окрестности кривой ![]() .
.
Так как в реальной действительности время течет в положительном направлении, то на практике реализуются те периодические движения, которым соответствуют устойчивые предельные циклы. Такие движения называются автоколебаниями.
Теорема 4. Пусть 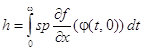 . (7)
. (7)
Если ![]() , то
, то ![]() является устойчивым предельным циклом; если
является устойчивым предельным циклом; если ![]() , то
, то ![]() — неустойчивый предельный цикл.
— неустойчивый предельный цикл.
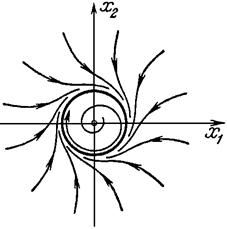
Характер приближения соседних траекторий к ![]() при
при ![]() следующий: они приближаются к
следующий: они приближаются к ![]() , образуя бесконечное число витков спирали, как изнутри, так и снаружи.
, образуя бесконечное число витков спирали, как изнутри, так и снаружи.
Похожие работы
... пакетах. Заключение Результатом выполнения курсового проекта является готовый программный продукт, позволяющий решать задачу Коши для системы дифференциальных уравнений при помощи неявной схемы Адамса 3-го порядка, демонстрирующий возможности численного решения поставленной задачи с заданной степенью точности. Готовый программный продукт может найти широкое применение при решении многих ...
... в векторно-матричной форме записи имеет следующий вид: . В таблице приведены результаты вычисления переходных процессов для векторно-матричного неоднородного дифференциального уравнения по формуле аналитического решения и трем рекуррентным выражениям, использующим различные квадратурные формулы интегрирования. Для заполнения таблицы с шагом 0.1 по третьей рекуррентной формуле второе ...
... при финансовой поддержке государственной научно-технической программы «Физика квантовых и волновых процессов» (проект 1.61) и физического учебно-научного центра «Фундаментальная оптика и спектроскопия». 1. Асимптотическое поведение решений дифференциальных уравнений с малым параметром Многие колебательные системы описываются дифференциальными уравнениями с малым параметром при производных: ...
... была построена теория вложения функциональных пространств, которые в настоящее время носят название пространств Соболева. А.Н. Тихоновым была построена теория некорректных задач. Выдающийся вклад в современную теорию дифференциальных уравнений внесли российские математики Н.Н. Боголюбов, А.Н. Колмогоров, И.Г. Петровский, Л.С. Понтрягин, С.Л. Соболев, А.Н. Тихонов и другие. Влияние на развитие ...
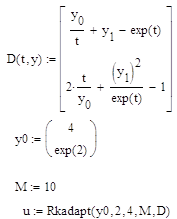
0 комментариев