Навигация
Теоремы второго метода Ляпунова
3.2. Теоремы второго метода Ляпунова.
Теорема 1. Пусть существует определенно-положительная функция Ляпунова ![]() , такая, что DV есть отрицательная функция. Тогда решение
, такая, что DV есть отрицательная функция. Тогда решение ![]() уравнения (1) устойчиво по Ляпунову.
уравнения (1) устойчиво по Ляпунову.
Доказательство. Пусть — произвольная положительная постоянная, ![]() . Положим
. Положим ![]() при
при ![]() . Так как V определенно-положительная, то
. Так как V определенно-положительная, то ![]() . По l найдем
. По l найдем ![]() такое, чтобы
такое, чтобы ![]() . Рассмотрим решение
. Рассмотрим решение ![]() при
при ![]() . Покажем, что
. Покажем, что
![]() . (5)
. (5)
Пусть (5) не имеет места. Тогда существует ![]() такое, что
такое, что ![]() , а при
, а при ![]() . В силу (3) и условия теоремы функция
. В силу (3) и условия теоремы функция ![]() является при
является при ![]() невозрастающей функцией t. Так как
невозрастающей функцией t. Так как ![]() , то
, то ![]() , тогда тем более
, тогда тем более ![]() , что противоречит определению T и тому, что
, что противоречит определению T и тому, что ![]() . Таким образом, импликация (5) имеет место, а это и означает по определению устойчивость решения
. Таким образом, импликация (5) имеет место, а это и означает по определению устойчивость решения ![]() по Ляпунову. Теорема доказана.
по Ляпунову. Теорема доказана.
Следствие. Если уравнение (1) имеет в области G определенно-положительный интеграл, не зависящий от t и уничтожающийся в начале координат, то решение ![]() устойчиво по Ляпунову.
устойчиво по Ляпунову.
Теорема 2. Пусть существует определенно-положительная функция Ляпунова ![]() , такая, что DV определенно-отрицательная при
, такая, что DV определенно-отрицательная при ![]() . Тогда решение
. Тогда решение ![]() уравнения (1) асимптотически устойчиво.
уравнения (1) асимптотически устойчиво.
Доказательство. Условия теоремы 1 выполнены, и решение ![]() устойчиво по Ляпунову. Следовательно, существует
устойчиво по Ляпунову. Следовательно, существует ![]() такое, что
такое, что
![]() при
при ![]() . (6)
. (6)
Из определения асимптотической устойчивости в силу (4) заключаем, что достаточно доказать импликацию ![]() при
при ![]() . В силу (3) и условия теоремы
. В силу (3) и условия теоремы ![]() — строго убывающая функция t.
— строго убывающая функция t.
Предположим, что теорема неверна. Тогда
![]() . (7)
. (7)
Отсюда, из (6) и (4) следует, что при ![]()
![]() . По условию теоремы
. По условию теоремы ![]() , где
, где ![]() — определенно-положительная функция. Пусть
— определенно-положительная функция. Пусть ![]() . Из (3) следует, что при всех
. Из (3) следует, что при всех ![]()
![]() , что противоречит определенной положительности
, что противоречит определенной положительности ![]() . Полученное противоречие доказывает теорему.
. Полученное противоречие доказывает теорему.
В случае когда уравнение автономно, условия теоремы (2) можно ослабить.
Теорема 3. Пусть уравнение (1) автономно, выполнены условия теоремы 1 и множество ![]() не содержит целиком полных траекторий уравнения (1), за исключением положения равновесия
не содержит целиком полных траекторий уравнения (1), за исключением положения равновесия ![]() . Тогда решение
. Тогда решение ![]() асимптотически устойчиво.
асимптотически устойчиво.
Доказательство. Используем доказательство теоремы 2 до формулы (7) включительно. Далее, пусть ![]() — -предельная точка траектории
— -предельная точка траектории ![]() . Из определения -предельной точки и (7) следует, что
. Из определения -предельной точки и (7) следует, что ![]() . По первому свойству предельных множеств (п. 1.3.) все точки траектории
. По первому свойству предельных множеств (п. 1.3.) все точки траектории ![]() являются -предельными для траектории
являются -предельными для траектории ![]() . Следовательно, для всех t, при которых определено решение
. Следовательно, для всех t, при которых определено решение ![]() ,
, ![]() . Отсюда и из (3) следует, что при указанных t
. Отсюда и из (3) следует, что при указанных t ![]() , что противоречит условию теоремы, так как
, что противоречит условию теоремы, так как ![]() не совпадает с началом координат. Теорема доказана.
не совпадает с началом координат. Теорема доказана.
Пример. Рассмотрим уравнение движения диссипативной системы с одной степенью свободы ![]() , где
, где ![]() удовлетворяют условию Липшица при
удовлетворяют условию Липшица при ![]() ,
, ![]() удовлетворяет условию
удовлетворяет условию ![]() при
при ![]() и
и ![]() при
при ![]() . Докажем, что положение равновесия
. Докажем, что положение равновесия ![]() асимптотически устойчиво.
асимптотически устойчиво.
Соответствующая система двух уравнений имеет вид
![]() .
.
В качестве функции Ляпунова возьмем полную энергию системы  .
.
В силу условия ![]() V —определенно-положительная функция, при этом
V —определенно-положительная функция, при этом
![]() .
.
Следовательно, DV —отрицательная функция и множество M — интервал оси абсцисс при ![]() . Так как при
. Так как при ![]() при
при ![]() , то множество M не содержит целых траекторий, отличных от положения равновесия
, то множество M не содержит целых траекторий, отличных от положения равновесия ![]() .
.
По теореме 3 решение ![]() системы асимптотически устойчиво, что и требовалось доказать.
системы асимптотически устойчиво, что и требовалось доказать.
Перейдем к рассмотрению неустойчивости. Пусть ![]() — функция Ляпунова. Обозначим через
— функция Ляпунова. Обозначим через ![]() любую связную компоненту открытого множества
любую связную компоненту открытого множества ![]() с началом координат на ее границе.
с началом координат на ее границе.
Теорема 4. Пусть существует функция Ляпунова ![]() такая, что
такая, что ![]() не пусто и при
не пусто и при ![]() . Тогда решение
. Тогда решение ![]() уравнения (1) неустойчиво.
уравнения (1) неустойчиво.
Доказательство. Пусть ![]() . Будем рассматривать решения
. Будем рассматривать решения ![]() с начальной точкой
с начальной точкой ![]() . Достаточно показать, что для каждого из этих решений можно указать момент T (для каждого решения свой) такой, что
. Достаточно показать, что для каждого из этих решений можно указать момент T (для каждого решения свой) такой, что ![]() .
.
Пусть это неверно, т. е. существует решение ![]() , удовлетворяющее при всех
, удовлетворяющее при всех ![]() неравенству
неравенству ![]() . Покажем, что траектория решения
. Покажем, что траектория решения ![]() принадлежит
принадлежит ![]() при
при ![]() . Действительно, по определению
. Действительно, по определению ![]() она может покинуть область
она может покинуть область ![]() только через ту часть ее границы, где
только через ту часть ее границы, где ![]() . Но это невозможно, так как
. Но это невозможно, так как ![]() и при возрастании
и при возрастании ![]() функция
функция ![]() строго возрастает, пока
строго возрастает, пока ![]() , в силу (3).
, в силу (3).
Итак, доказано, что при ![]()
![]() и
и ![]() . Следовательно, по условию теоремы
. Следовательно, по условию теоремы ![]() при
при ![]() . Интегрируя (3) от
. Интегрируя (3) от ![]() до
до ![]() , получаем
, получаем
![]() ,
,
что противоречит ограниченности ![]() при
при ![]() . Противоречие доказывает теорему.
. Противоречие доказывает теорему.
Пример. Рассмотрим уравнение ![]() , где
, где ![]() — удовлетворяющая условию Липшица при
— удовлетворяющая условию Липшица при ![]() функция такая, что
функция такая, что ![]() при
при ![]() . Докажем неустойчивость решения
. Докажем неустойчивость решения ![]() .
.
Рассмотрим систему ![]() , соответствующую уравнению примера. В качестве функции Ляпунова возьмем
, соответствующую уравнению примера. В качестве функции Ляпунова возьмем ![]() . Имеем:
. Имеем:
![]() .
.
По теореме 4 решение ![]() системы неустойчиво, что и требовалось доказать.
системы неустойчиво, что и требовалось доказать.
Похожие работы
... пакетах. Заключение Результатом выполнения курсового проекта является готовый программный продукт, позволяющий решать задачу Коши для системы дифференциальных уравнений при помощи неявной схемы Адамса 3-го порядка, демонстрирующий возможности численного решения поставленной задачи с заданной степенью точности. Готовый программный продукт может найти широкое применение при решении многих ...
... в векторно-матричной форме записи имеет следующий вид: . В таблице приведены результаты вычисления переходных процессов для векторно-матричного неоднородного дифференциального уравнения по формуле аналитического решения и трем рекуррентным выражениям, использующим различные квадратурные формулы интегрирования. Для заполнения таблицы с шагом 0.1 по третьей рекуррентной формуле второе ...
... при финансовой поддержке государственной научно-технической программы «Физика квантовых и волновых процессов» (проект 1.61) и физического учебно-научного центра «Фундаментальная оптика и спектроскопия». 1. Асимптотическое поведение решений дифференциальных уравнений с малым параметром Многие колебательные системы описываются дифференциальными уравнениями с малым параметром при производных: ...
... была построена теория вложения функциональных пространств, которые в настоящее время носят название пространств Соболева. А.Н. Тихоновым была построена теория некорректных задач. Выдающийся вклад в современную теорию дифференциальных уравнений внесли российские математики Н.Н. Боголюбов, А.Н. Колмогоров, И.Г. Петровский, Л.С. Понтрягин, С.Л. Соболев, А.Н. Тихонов и другие. Влияние на развитие ...
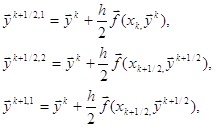
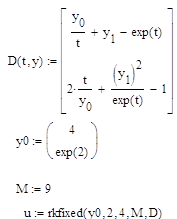
0 комментариев