Маршруты на БАС

3.1.3. Маршруты на БАС

Применение блочно-альтернативных сетей  для решения различного рода задач (анализ, синтез, классификация и т.д.) основано на использовании их свойства порождать множество альтернативных маршрутов М_N. При описании допустимых множеств маршрутов М_N на сетях , целесообразно исходить из блочной структуры альтернативной сети.

В БАС используется вершинный тип маршрутов. С точки зрения сети маршруты подразделяются на внутриблоковые и сетевые. Послед­ние, в свою очередь, формируются из внутриблоковых и межблоковых.

Внутриблоковый – это такой маршрут Мⁱ_N М_N (i = 1, …, n), который тем или иным образом связывает две соседние вершины () первого ранга, принадлежащие i-му блоку. Другими словами, внутриблоковый маршрут формируется как последовательность вершин, связанных определенным отношением.

Межблоковые – маршруты М^il_N , которые связывают некоторые пары вершин первого ранга {(), i = 1, …, n; k = 1, 2, …, n;  }. Межблоковые маршруты используются при формировании циклов, и, следовательно, связываемые вершины () для таких маршрутов отождествляются.

При использовании БАС для решения конкретных задач могут возникать ситуации, когда тот или иной внутриблоковый маршрут Мⁱ_N формируется неоднозначным образом. При этом возможны три случая:

1) внутриблоковый маршрут Мⁱ_N проходится один раз слева направо;

2) внутриблоковый маршрут Мⁱ_N для маршрута М_N  является запрещенным;

3) внутриблоковый маршрут Мⁱ_N должен быть пройден неоднократно.

В соответствии с названными случаями, определим три типа маршрутов: ациклические AMⁱ_N, транзитные ТMⁱ_N и циклические СMⁱ_N.

Ациклические маршруты

Наиболее простыми маршрутами М_N    являются ациклические (или незамкнутые) AMⁱ_N.

Ациклический маршрут (АМⁱ) формируется как последовательность

вершин совместно с отношением между вершинами:

AMⁱ : (Aⁱ, r_ij , a_ij),

где Аⁱ - атрибут;

r_ij - определяет отношение между атрибутом и вершиной-значе­нием a_ij;

a_ij - значение атрибута Аⁱ.

Полное представление внутриблокового маршрута по схеме ис­ток-сток будет представлять собой объединение:

AMⁱ : (Аⁱ , r_ij ,a_ij) U (a_ij ,r_ji ,A*_i),

или в общем виде для вершин-альтернатив получим вершинный ацикли­ческий маршрут:

AMⁱ: (Аⁱ, a_ij, A*_i).

Аналогично для маршрута, проходящего через транзитивную верши­ну:

АMⁱ_T: (Aⁱ, r_T, A*_i),

что эквивалентно записи

AMⁱ_T: (Aⁱ, T, A*_i).

Ациклические маршруты имеют место в тех случаях, когда осуществляется однократное прохождение слева направо через блок , между блоками (,) или по сети  в целом.

Внутриблоковые ациклические маршруты всегда проходят через вершины (j = 1,2, … , m; i = 1,2, … , n) второго ранга. В общем случае маршрут AMⁱ_N может быть задан последовательностью:

AMⁱ_N= {(); (j = 1,2, … , m; I = 1, 2, …, n)}

В этой последовательности и обозначают дуги между соответствующими парами вершин внутри i-го блока. Кратко это выражение можно записать так:

AMⁱ_N=  (3.1)

Отметим, что на сети любой внутриблоковый маршрут AMⁱ_Nвсегда начинается с входной вершины .

Транзитные маршруты

Достаточно часто при использовании сети  могут возникать случаи, когда прохождение через блок  (i = 1, 2, …, n) или совокупность блоков  запрещено. Иными словами, запрещены в рассмотренном выше смысле ациклические маршруты AMⁱ_Nили AM^i,l_N, при этом полные маршруты AM_N  имеют место.

Для описания подобного рода случаев введено понятие транзитного маршрута ТМ_N (для сети в целом понятие транзитного маршрута не имеет смысла.) Прежде чем дать определение транзитного внутриблокового маршрута ТMⁱ_N, введем и определим понятие транзитной вершины . Транзитными являются такие вершины (i = 1, 2, …, n) второго ранга, которые не несут семантической нагрузки в соответствии с признаком , а определяют лишь маршрут следования внутри блока  . Таким образом, внутриблоковым транзитным маршрутом является ТMⁱ_Nтакой маршрут, который проходит через транзитную вершину. В общем случае внутриблоковый транзитный маршрут ТMⁱ_Nопределяется последовательностью:

ТMⁱ_N=

или в сокращенной форме: ТMⁱ_N=.

Циклические маршруты

 В тех случаях, когда осуществляется неоднократное прохождение через блок  (i = 1, 2, …, n) или {(,), l = i+k, k 1} или через сеть в целом, то имеют место циклические маршруты.

Основой циклических маршрутов СMⁱ_Nявляются ациклические АMⁱ_N.Замыкание внутриблокового маршрута АMⁱ_N осуществляется через вершины (), которые соответственно определяют конец и начало. В общем случае для любого блока  циклические маршруты СMⁱ_N можно представить виде суммы соответствующих ациклических маршрутов АMⁱ_N, каждый из которых повторен  раз. Используя выражение (3.1), можно записать:

СMⁱ_N,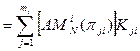

где К_ji0 – количество j-х циклов в i-ом блоке.

Внутриблоковые циклические маршруты СMⁱ_Nиспользуются в тех случаях, когда при формировании маршрута M_N  возникает необходимость неоднократного прохождения через какой-либо блок  с целью включения в такой маршрут любого количества любых вершин

 (j = 1,2, … , m; i = 1,2, … , n).

Межблоковые и сетевые маршруты формируются на основе склеива­ния внутриблоковых. Для этих целей используются специальные алго­ритмы, которые осуществляют как формирование самого маршрута, так и склеивание внутриблоковых в единый сетевой:

M_Na, = U (MБi),

где MN_a - сетевой маршрут;

MБi - внутриблоковый маршрут.

При таком алгоритме навигации путем склеивания будет получен маршрут MN_a  со своим набором решений:

R = (R_1,, …, R_i, …, R_N)

Для каждого блока альтернатив определяется свой алгоритм вы­бора альтернативы. Алгоритм параллельной навигации, в свою оче­редь, реализует функции координации, которые взаимодействуют с каждым блоковым алгоритмом. Работа осуществляется параллельно. Алгоритм координации передает исходные данные в локальные алгоритмы и запускает их в работу. Каждый из локальных алгоритмов формирует внутриблоковый маршрут и получает соответствующий результат (R). Далее формируется последовательность (R¹₁, ..., Rⁱ₁, ..., R^N₁) = R_l несвязанных между собой решений. После этого решается задача склеивания частных решений в общее. Данная процедура может проте­кать по двум направлениям:

1) формирование общего решения на уровне координирующего ал­горитма; анализ, оценка, принятие решения для дальнейших дейс­твий;

2) координирующий алгоритм решает задачу общего решения, од­новременно выдав задание блоковым алгоритмам на формирование частных решений. При получении общих решений возможна параллель­ная стратегия для многоальтернативных решений.

Получив парадигму общих решений, в соответствии с определен­ными критериями выбирается наилучшее из них.