Навигация
Серийный отбор
2.2. Серийный отбор
Задача 1. В одном из цехов предприятия в десяти бригадах работает 100 рабочих. В целях изучения квалификации рабочих была проведена 20%-я серийная бесповторная выборка, в которую вошли 2 бригады. Получено следующее распределение обследованных рабочих по разрядам:
Таблица 2.5
| Номер | Разряды рабочих | |
| рабочего | в бригаде 1 | в бригаде 2 |
| 1 2 3 4 5 6 7 8 9 10 | 2 4 5 2 5 6 5 8 4 5 | 3 6 1 5 3 4 2 1 3 2 |
Определить с вероятностью 0,997 предел, в котором находится средний разряд рабочих цеха.
Решение.
Средняя ошибка выборочной средней (см.табл.1.2) определяется по следующей формуле:
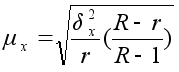 ,
,
где
![]() – межсерийная
дисперсия
выборочных
средних;
– межсерийная
дисперсия
выборочных
средних;
R – число серий в генеральной совокупности;
r – число отобранных серий.
Для определения межсерийной (межгрупповой) дисперсии выборочных средних необходимо рассчитать групповые и общую среднюю величину.
Средний разряд:
в первой бригаде
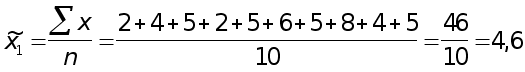 разр.
разр.
во второй бригаде
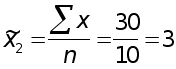 разр.
разр.
Средний разряд рабочего в двух бригадах (общая средняя)
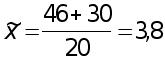 разр.
разр.
Межсерийная (межгрупповая) дисперсия
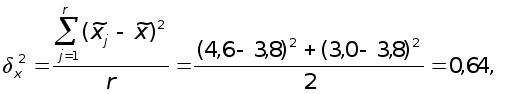
где
![]() – среднее значение
показателя в j
– й серии (группе);
– среднее значение
показателя в j
– й серии (группе);
![]() – среднее
значение показателя
во всех сериях
(общая средняя).
– среднее
значение показателя
во всех сериях
(общая средняя).
Средняя ошибка среднего разряда рабочего в двух бригадах (выборочной средней)
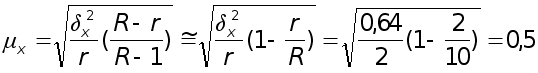 разр.
разр.
Значению
вероятности
0,997 соответствует
значение гарантийного
коэффициента
![]() Тогда предельная
ошибка выборочной
средней
Тогда предельная
ошибка выборочной
средней
![]() разр.
разр.
С вероятностью
0,997 можно утверждать,
что средний
разряд рабочих
цеха находится
в пределах
![]()
Задача 2. Детали упакованы в 200 ящиков по 40 деталей в каждый. Для проверки качества деталей был проведен сплошной контроль деталей в 20 ящиках (10%-й серийный бесповторный отбор). В результате контроля установлено, что доля бракованных деталей составляет 15%. Межсерийная дисперсия равна 0,002.
С вероятностью 0,954 определить пределы, в которых находится доля бракованной продукции во всей партии ящиков.
Решение.
Средняя ошибка выборочной доли (см.табл.1.2)
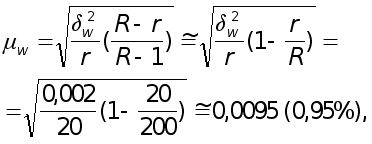
где
![]() – межсерийная
дисперсия
выборочной
доли.
– межсерийная
дисперсия
выборочной
доли.
Предельная
ошибка выборочной
доли (доли
бракованных
деталей в выборке)
с вероятностью
0,954 (гарантийный
коэффициент![]() )
составит
)
составит
![]()
С вероятностью 0,954 можно утверждать, что доля дефектной продукции в партии (в 200 ящиках) находится в пределах
![]()
Задача 3. В механическом цехе предприятия имеется 10 бригад по 20 рабочих в каждой бригаде. Для установления квалификации (среднего разряда) рабочих цеха используется метод серийного бесповторного отбора.
Определить необходимое количество бригад, чтобы с вероятностью 0,997 ошибка выборки (средний разряд рабочего в цехе) не превышала одного разряда. На основе предыдущих исследований известно, что межсерийная дисперсия равна 0,9.
Решение.
С вероятностью
0,997 (гарантийный
коэффициент
![]() )
численность
выборочной
совокупности
(число отобранных
бригад) определяется
следующим
образом (см.табл1.3):
)
численность
выборочной
совокупности
(число отобранных
бригад) определяется
следующим
образом (см.табл1.3):
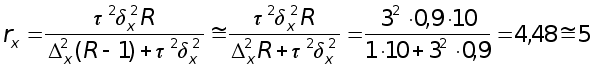 бр.
бр.
Задача 4. На предприятии работает 200 бригад с одинаковой численностью рабочих. Для изучения доли рабочих, выполняющих норму выработки, используется метод серийного бесповторного отбора.
Определить необходимую численность выборки, чтобы с вероятностью 0,954 предельная ошибка выборки (предельная ошибка доли рабочих, выполняющих норму выработки) не превышала 5%, если межсерийная дисперсия выборочной доли равна 2,25.
Решение.
Необходимая
численность
выборки
для изучения
выборочной
доли (см.табл.1.3)
с вероятностью
0,954 (гарантийный
коэффициент![]() )
равна
)
равна
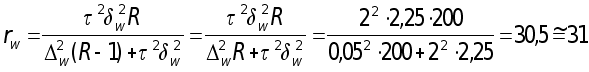 бр.
бр.
Задача 5. Для определения средней наработки до отказа 1000 приборов, распределенных на партии (серии) по 10 шт., проводится серийная 4%-я бесповторная выборка. Результаты испытаний отобранных приборов характеризуются следующими данными:
Таблица 2.6
| Показатели | Номер партии приборов | |||
| 1 | 2 | 3 | 4 | |
| Средняя наработка до отказа, тыс.ч Доля приборов с наработкой до отказа не менее 12 тыс.ч | 10 0,80 | 12 0,85 | 15 0,90 | 18 0,95 |
Определить:
1) средние ошибки репрезентативности:
- наработки приборов до отказа;
- удельного веса приборов с наработкой до отказа не менее 12 тыс.ч;
2) с вероятностью 0,954 пределы, в которых будет находиться:
- средняя наработка до отказа всех приборов;
- доля приборов в генеральной совокупности, наработка до отказа которых не менее 12 тыс.ч;
3) вероятность того, что
- предельная ошибка выборки при установлении средней наработки до отказа не превысит 1,0 тыс.ч;
- доля приборов с наработкой до отказа не менее 12 тыс.ч будет находиться в пределах от 83% до 92%.
Решение.
Похожие работы
... будут находиться характеристики генеральной совокупности. 9. Формулы для расчета необходимого объема выборки. 10. Сущность теорем П.Л. Чебышева и А.М. Ляпунова. 11. Распространение результатов выборочного наблюдения на генеральную совокупность. 2.5. Тесты 1. Совокупность, из которой производится отбор единиц для выборочного наблюдения называется: а) выборочной; б) генеральной; ...
... 1. Сущность и виды обобщающих статистических показателей. 2. Абсолютные статистические показатели, их значение в статистике и единицы измерения. 3. Виды относительных величин, техника их расчета и формы выражения. 4. Зависимость между относительными величинами динамики и планового задания. 5. Что выражают относительные величины структуры и координации. 6. Для характеристики каких ...
... Таблица 1 Среднее значение интервала, тыс. грн Фактическое количество предприятий 16 9 20 45 24 16 28 24 32 18 36 12 40 6 Всего 100 Тесты для закрепления материала Тест 1 В статистике критерий Стьюдента обозначается: а) критерий; б) ; в) критерий. Тест 2 Мощность критерия – это: а) вероятность отклонения испытуемой нулевой гипотезы, когда правильною является ...
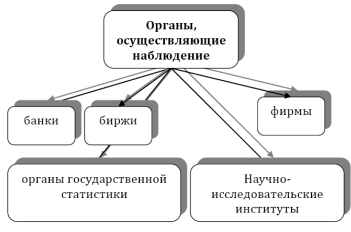
... учитывается по месту жительства, а не по месту работы [4, 6]. Наблюдение может проводиться собственными силами или организациями, специализирующимися на проведении наблюдений. Проводят наблюдение как органы государственной, так и ведомственной статистики. Рис.2. Органы, которые могут проводить наблюдение [1] В зависимости от особенностей объекта при организации статистического наблюдения ...
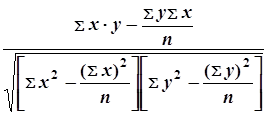

0 комментариев