Навигация
Ошибка выборочной доли
4.3.2. Ошибка выборочной доли
Выборочная доля представляет собой отношение числа единиц, обладающих данным признаком или данным его значением ( m ) к общему числу единиц выборочной совокупности ( n )
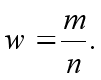
(Эту статистическую характеристику не следует путать с долей выборки, являющейся отношением числа единиц выборочной совокупности к числу единиц генеральной совокупности).
Ошибка выборочной доли представляет собой расхождение (разность) между долей в выборочной совокупности ( w ) и долей в генеральной совокупности ( p ), возникающее вследствие несплошного характера наблюдения. Величина ошибки выборочной доли определяется как предел отклонения w от p , гарантируемый с заданной вероятностью:
![]()
где
![]() – гарантийный
коэффициент,
зависящий от
вероятности
– гарантийный
коэффициент,
зависящий от
вероятности ![]() , с которой
гарантируется
невыход разности w –p за пределы
, с которой
гарантируется
невыход разности w –p за пределы
![]() ;
;
![]() – средняя ошибка
выборочной
доли.
– средняя ошибка
выборочной
доли.
Средняя ошибка выборочной доли определяется по формуле
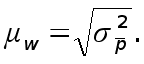
Или, как было доказано выше,
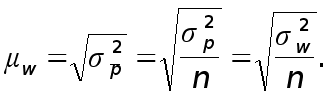
где ![]() – дисперсия
доли в генеральной
совокупности
(дисперсия
генеральной
доли);
– дисперсия
доли в генеральной
совокупности
(дисперсия
генеральной
доли);
![]() – дисперсия
доли в выборке
(дисперсия
выборочной
доли).
– дисперсия
доли в выборке
(дисперсия
выборочной
доли).
Приведенная формула средней ошибки выборочной доли применяется при повторном отборе.
Для определения дисперсии альтернативного признака допустим, что общее число единиц совокупности равно n . Число единиц, обладающих данным признаком - f , тогда число единиц, не обладающих данным признаком, равно n-f . Ряд распределения качественного (альтернативного) признака
| Значение переменной | Частота повторений |
| 1 0 | f n-f |
| Итого | n |
Средняя арифметическая такого ряда равна:
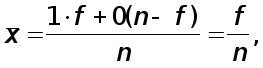
то
есть равна
относительной
частолте (частости)
появления
данного признака,
которую можно
обозначить
через p , тогда ![]()
Таким образом, доля единиц, обладающих данным признаком равна p ; соответственно доля единиц, не обладающих данным признаком, равна q ; p+q =1. Тогда дисперсия альтернативного признака определяется по формуле
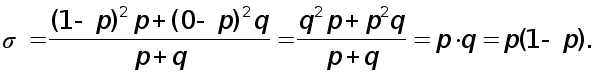
Для показателя доли альтернативного признака в выборке (выборочной доли) дисперсия определяется по формуле
![]()
При
бесповторном
отборе численность
генеральной
совокупности
сокращается,
поэтому дисперсия
умножается
на коэффициент
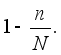 Формулы расчета
средних ошибок
выборочной
доли для различных
способов отбора
единиц из генеральной
совокупности
приведены в
табл. 4.2; 3 и 4.
Формулы расчета
средних ошибок
выборочной
доли для различных
способов отбора
единиц из генеральной
совокупности
приведены в
табл. 4.2; 3 и 4.
Дисперсии в формулах расчета средних ошибок выборочной доли в табл.4.2. рассчитываются следующим образом:
– межсерийная дисперсия выборочной доли
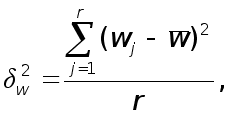
где wj – выборочная доля в j –й серии;
![]() – средняя
величина доли
во всех сериях;
– средняя
величина доли
во всех сериях;
– средняя из групповых дисперсий
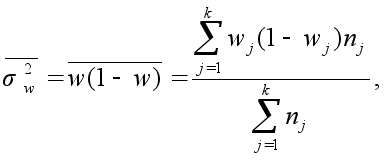
где wj – выборочная доля в j –й типической группе;
nj – число единиц в j –й типической группе;
k – число типических групп.
Для случая, когда доля (частость) даже приблизительно неизвестна, можно произвести "грубый" расчет средней ошибки выборки для доли, используя в расчете максимальную величину дисперсии доли, равную 0,25. Тогда для
повторного отбора
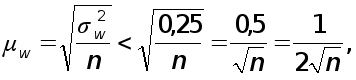
бесповторного отбора
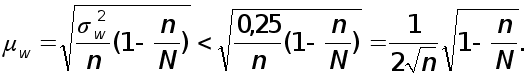
Предельное значение ошибки выборочной доли определяется по следующей формуле:
![]()
Величина
средней ошибки
выборочной
доли
![]() зависит
от доли изучаемого
признака в
генеральной
совокупности,
числа наблюдений
и способа отбора
единиц из генеральной
совокупности
для наблюдения,
а величина
предельной
ошибки
зависит
от доли изучаемого
признака в
генеральной
совокупности,
числа наблюдений
и способа отбора
единиц из генеральной
совокупности
для наблюдения,
а величина
предельной
ошибки
![]() зависит еще
и от величины
вероятности
зависит еще
и от величины
вероятности
![]() ,
с которой
гарантируются
результаты
выборочного
наблюдения.
,
с которой
гарантируются
результаты
выборочного
наблюдения.
Распространение
выборочных
данных на генеральную
совокупность
производится
с учетом доверительных
интервалов.
Доля альтернативного
признака в
генеральной
совокупности
равна![]()
Пример
Сущность процесса случайного отбора и основные свойства простой повторной выборки можно показать на условном примере.
Генеральная совокупность состоит из трех единиц ( N = 3 ), например
| Порядковый номер рабочего | 1 | 2 | 3 | 4 |
| Тарифный разряд, xi | 3 | 4 | 4 | 5 |
Генеральная средняя
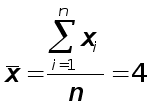 разряд;
разряд;
генеральная дисперсия
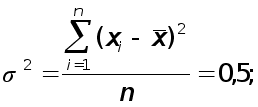
доля рабочих в генеральной совокупности, имеющих 4 тарифный разряд
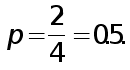
Задача. Определить параметры генеральной совокупности ( средний разряд, дисперсию и долю рабочих с тарифным разрядом, равным 4) по результатам проведения простой случайной повторной выборки объемом 2 единицы ( n = 2 ).
В данном примере с одинаковой степенью вероятности могла бы появиться любая из 16 возможных комбинаций единиц, то есть любая из 16 возможных выборок. Результаты 16 выборок приведены в табл. 1
Таблица 1
| Номер выборки | Номера единиц, входящих в выборку | Значения признака по данным выборки | Выборочная средняя
| Отклонение выборочной средней от генеральной средней | Выбо- рочная доля
|
| 1 | 1; 1 | 3; 3 | 3,0 | -1,0 | 0,0 |
| 2 | 1; 2 | 3; 4 | 3,5 | -0,5 | 0,5 |
| 3 | 1; 3 | 3; 4 | 3,5 | -0,5 | 0,5 |
| 4 | 1; 4 | 3; 5 | 4,0 | 0,0 | 0,0 |
| 5 | 2; 1 | 4; 3 | 3,5 | -0,5 | 0,5 |
| 6 | 2; 2 | 4; 4 | 4,0 | 0,0 | 1,0 |
| 7 | 2; 3 | 4; 4 | 4,0 | 0,0 | 1,0 |
| 8 | 2; 4 | 4; 5 | 4,5 | +0,5 | 0,5 |
| 9 | 3; 1 | 4; 3 | 3,5 | -0,5 | 0,5 |
| 10 | 3; 2 | 4; 4 | 4,0 | 0,0 | 1,0 |
| 11 | 3; 3 | 4; 4 | 4,0 | 0,0 | 1,0 |
| 12 | 3; 4 | 4; 5 | 4,5 | +0,5 | 0,5 |
| 13 | 4; 1 | 5; 3 | 4,0 | 0,0 | 0,0 |
| 14 | 4; 2 | 5; 4 | 4,5 | +0,5 | 0,5 |
| 15 | 4; 3 | 5; 4 | 4,5 | +0,5 | 0,5 |
| 16 | 4; 4 | 5; 5 | 5,0 | +1,0 | 0,0 |
Возможные варианты значений выборочных средних и отклонения их от генеральной средней представлены в виде ряда распределения (табл.2)
Таблица 2
| Выборочные средние разряды рабочих
| Число выборок с данной выборочной средней fj | Отклонение выборочной средней от генеральной средней
| Вероятность появления данного значения выборочной средней (или величины отклонения выборочной средней от генеральной) |
| 3,0 | 1 | -1,0 | 0,0625 |
| 3,5 | 4 | -0,5 | 0,2500 |
| 4,0 | 6 | 0,0 | 0,3750 |
| 4,5 | 4 | +0,5 | 0,2500 |
| 5,0 | 1 | +1,0 | 0,0625 |
| Итого | 16 | 1,0000 |
В распределении величин выборочных средних и их отклонений наблюдаются определенные закономерности.
1. Из возможных результатов случайной повторной выборки наиболее вероятны такие, при которых величина выборочной средней будет близка к величине генеральной средней. Таким образом, чем больше величина случайной ошибки выборки, тем менее вероятно появление такой ошибки.
2. В примере не встречаются ошибки больше единицы по абсолютной величине, т.е. всегда существует предел расхождений между выборочной и генеральной средней.
По данным табл.2, где представлены все возможные варианты выборочных средних и их отклонения от генеральной средней, определяется величина стандартной ошибки выборки
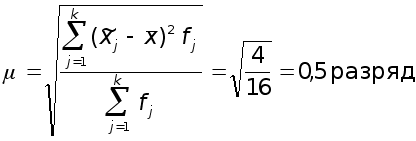
Однако на практике исследователь оперирует данными какой-то одной конкретной выборки, а поэтому указанным способом определить стандартную ошибку средней невозможно.
Среднюю ошибку можно определить по формуле, используя величину дисперсии в генеральной совокупности (в данном примере генеральная дисперсия признака равна 0,5)
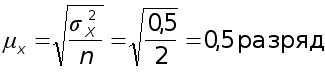
Распределение выборочной доли представлено в табл.3
Таблица 3
| Выборочная доля
| Число выборок с данной выборочной долей fj | Отклонение выборочной доли от генеральной
|
|
|
| 0,0 | 4 | -0,5 | 0,0 | 1,0 |
| 0,5 | 8 | 0,0 | 4,0 | 0,0 |
| 1,0 | 4 | +0,5 | 4,0 | 1,0 |
| Итого | 16 | 8,0 | 2,0 |
В среднем для всех возможных вариантов выборок величина выборочной доли совпадает с долей признака в генеральной совокупности
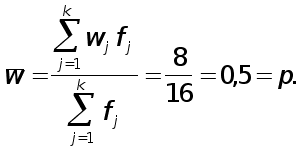
Средняя квадратическая ошибка доли в генеральной совокупности
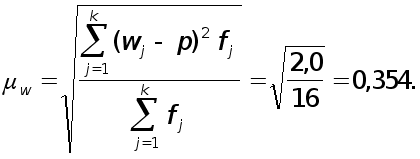
Среднюю квадратическую ошибку доли в генеральной совокупности можно определить, используя долю признака в генерального совокупности ( p = 0,5),
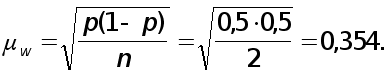
В формулы средних ошибок выборки
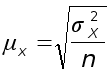 ;
; 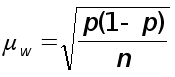
входят дисперсии признака и доли в генеральной совокупности, величины которых, как правило, при проведении выборочного наблюдения неизвестны. Поэтому для расчета средних ошибок выборки приходится использовать выборочные дисперсии в качестве оценки генеральной совокупности.
Похожие работы
... будут находиться характеристики генеральной совокупности. 9. Формулы для расчета необходимого объема выборки. 10. Сущность теорем П.Л. Чебышева и А.М. Ляпунова. 11. Распространение результатов выборочного наблюдения на генеральную совокупность. 2.5. Тесты 1. Совокупность, из которой производится отбор единиц для выборочного наблюдения называется: а) выборочной; б) генеральной; ...
... 1. Сущность и виды обобщающих статистических показателей. 2. Абсолютные статистические показатели, их значение в статистике и единицы измерения. 3. Виды относительных величин, техника их расчета и формы выражения. 4. Зависимость между относительными величинами динамики и планового задания. 5. Что выражают относительные величины структуры и координации. 6. Для характеристики каких ...
... Таблица 1 Среднее значение интервала, тыс. грн Фактическое количество предприятий 16 9 20 45 24 16 28 24 32 18 36 12 40 6 Всего 100 Тесты для закрепления материала Тест 1 В статистике критерий Стьюдента обозначается: а) критерий; б) ; в) критерий. Тест 2 Мощность критерия – это: а) вероятность отклонения испытуемой нулевой гипотезы, когда правильною является ...
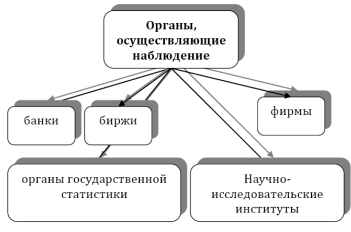
... учитывается по месту жительства, а не по месту работы [4, 6]. Наблюдение может проводиться собственными силами или организациями, специализирующимися на проведении наблюдений. Проводят наблюдение как органы государственной, так и ведомственной статистики. Рис.2. Органы, которые могут проводить наблюдение [1] В зависимости от особенностей объекта при организации статистического наблюдения ...
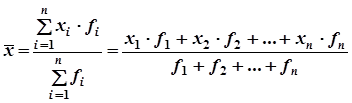

0 комментариев