Навигация
Малая выборка
4.5. Малая выборка
Под малой выборкой понимается такое выборочное наблюдение, численность единиц которого не превышает 20–30 и может составлять 5–6. С увеличением численности выборочной совокупности повышается точность выборочных данных, однако приходится иногда ограничиваться малым числом наблюдений. Эта необходимость возникает, например, при проверке качества продукции, связанной с уничтожением проверяемой единицы продукции. В математической статистике доказывается, что при малых выборках характеристики выборочной совокупности можно распространять на генеральную, но расчет средней и предельной ошибок выборки имеет особенности.
Ранее указывалось,
что при большом
объеме выборочной
совокупности (n
> 100) коэффициент
![]() ,
на который
необходимо
умножить выборочную
дисперсию,
чтобы получить
генеральную,
не играет большой
роли. Но когда
выборочная
совокупность
небольшая, этот
коэффициент
необходимо
принимать во
внимание. Средняя
ошибка малой
выборки (
,
на который
необходимо
умножить выборочную
дисперсию,
чтобы получить
генеральную,
не играет большой
роли. Но когда
выборочная
совокупность
небольшая, этот
коэффициент
необходимо
принимать во
внимание. Средняя
ошибка малой
выборки ( ![]() )
вычисляется
по формуле
)
вычисляется
по формуле
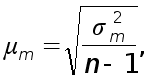
где
![]() – дисперсия
в малой выборке,
которая определяется
следующим
образом:
– дисперсия
в малой выборке,
которая определяется
следующим
образом:
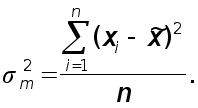
Предельная ошибка имеет вид
![]()
Значение
коэффициента
доверия ![]() зависит не
только от заданной
доверительной
вероятности,
но и от численности
единиц выборки n . Английский
ученый Стьюдент
доказал, что
в случаях малой
выборки действует
особый закон
распределения
вероятности.
В табл.4.4 приводятся
значения,
характеризующие
вероятность
(
зависит не
только от заданной
доверительной
вероятности,
но и от численности
единиц выборки n . Английский
ученый Стьюдент
доказал, что
в случаях малой
выборки действует
особый закон
распределения
вероятности.
В табл.4.4 приводятся
значения,
характеризующие
вероятность
(![]() )
того, что предельная
ошибка малой
выборки не
превысит
)
того, что предельная
ошибка малой
выборки не
превысит ![]() –кратную
среднюю ошибку:
–кратную
среднюю ошибку:
![]()
Таблица 4.4
Распределение
вероятности
![]() в малых выборках
в зависимости
в малых выборках
в зависимости
от значения
коэффициента
![]() и численности
выборки
и численности
выборки
|
| n | ||||||
| 5 | 7 | 10 | 12 | 16 | 18 | 20 | |
1,0 1,5 2,0 2,5 3,0 | 0,626 0,792 0,884 0,933 0,960 | 0,644 0,816 0,908 0,953 0,976 | 0,657 0,832 0,923 0,966 0,985 | 0,662 0,838 0,930 0,970 0,988 | 0,666 0,846 0,936 0,975 0,991 | 0,668 0,848 0,938 0,977 0,992 | 0,670 0,850 0,940 0,978 0,993 |
Статистическая проверка гипотез
Ефимова М.Р., Петрова Е.В., Румянцев В.Н. Общая теория статистики:
Учебник. М.: ИНФРА-М, 1998. - 416 с. (стр.182-203)
1. Выбор критической области. Критерии согласия.
2. Проверка гипотезы о принадлежности "выделяющихся" наблюдений исследуемой генеральной совокупности.
3. Проверка гипотезы о величине средней арифметической и доли.
4. Проверка гипотезы о расхождении двух выборочных дисперсий (дисперсионный анализ).
ЛИТЕРАТУРА
1. Богородская Н.А. Статистика. Методы анализа статистической
информации: Текст лекций. СПб.: СПГААП. - 1997. - 80 с.
2. Ефимова М.Р., Петрова Е.В., Румянцев В.Н. Общая теория статистики:
Учебник. М.: ИНФРА-М, 1998. - 416 с.
3. Статистика: Курс лекций /Харченко Л.П., Долженкова В.Г., Ионин В.Г. и
др.; Под ред. В.Г.Ионина. - Новосибирск: Изд-во НГАЭиУ, 1996. - 310 с.
4. Общая теория статистики: Статистическая методология в изучении
коммерческой деятельности. Учебник /А.И.Харламов, О.Э.Башина,
В.Т.Бабурин и др.; Под ред.А.А.Спирина, О.Э.Башиной. М.: Финансы
статистика, 1994. - 296 с.
5. Гусаров В.М. Теория статистики. - М.: Аудит, 1998. - 247 с.
6. Елисеева И.И., М.М.Юзбашев. Общая теория статистики. - М.: Финансы и
статистика, 1998. - 367 с.
7. Теория статистики. Учебник/Под ред.Р.А.Шмойловой. - М.: Финансы и
статистика, 1998. - 576 с.
8. Ряузов Н.Н. Общая теория статистики: Учебник для студентов экономич.
спец. вузов. -4-е изд., перераб. и дополн. М.: Финансы и статистика, 1984.
- 343 с.
9. Общая теория статистики / Под ред.Гольберга А.М., Козлова В.С. - М.:
Финансы и статистика, 1986. - 367 с.
10. Общая теория статистики / Под ред.Боярского А.Я., Громыко Г.Л.. М.:
Изд-во МГУ, 1985. - 326 с.
11. Практикум по теории статистики: Учебное пособие./ Под ред.
Р.А.Шмойловой. - М.: Финансы и статистика, 1998. 416 с.
12. Сборник задач по общей теории статистики: Учебное пособие для
студентов вузов, обучающихся по специальности “Статистика” /
Овсиенко В.Е., Голованова Н.В., Королев Ю.Г. и др., -2-е изд., перераб. и
дополн. М.: Финансы и статистика, 1986. - 191 с.
13. Практикум по общей теории статистики /Под ред. Ряузова Н.Н. - 2-е изд.,
перераб.и дополн. М.: Финансы и статистика, 1981. - 278 с.
14. Вайнберг Дж., Шумекер Дж. Статистика. М.: Статистика, 1979. 389 с.
15. Венецкий И.Г., Венецкая В.И. Основные математико–статистические понятия и формулы в экономическом анализе. М.: Статистика, 1974. 278 с.
16. Кейн Э. Экономическая статистика и эконометрия. М.: Статистика, 1977. 229 с.
Приложение
Таблица случайных чисел
| 5489 | 5583 | 3156 | 0835 | 1988 | 3912 | 0938 | 7460 | 0869 | 4420 |
| 3522 | 0935 | 7877 | 5665 | 7020 | 9555 | 7375 | 7124 | 7878 | 5544 |
| 7555 | 7579 | 2550 | 2487 | 9477 | 0864 | 2349 | 1012 | 8250 | 2633 |
| 5759 | 3554 | 5080 | 9074 | 7001 | 6249 | 3224 | 6368 | 9102 | 2672 |
| 6303 | 6895 | 3371 | 3196 | 7231 | 2918 | 7380 | 0438 | 7547 | 2644 |
| 7351 | 5634 | 5323 | 2623 | 7803 | 8374 | 2191 | 0464 | 0696 | 9529 |
| 7068 | 7803 | 8832 | 5119 | 6350 | 0120 | 5026 | 3684 | 5657 | 0304 |
| 3613 | 1428 | 1796 | 8447 | 0503 | 5654 | 3254 | 7336 | 9536 | 19441 |
| 5143 | 4534 | 2105 | 0368 | 7890 | 2473 | 4240 | 8652 | 9435 | . 1422 |
| 9815 | 5144 | 7649 | 8638 | 6137 | 8070 | 5345 | 4865 | 2456 | 5708 |
| 5780 | 1277 | 6816 | 1013 | 2867 | 9938 | 3930 | 3203 | 5696 | 1769 |
| 1187" | 0951 | 5991 | 5245 | 5700 | 5564 | 7352 | 0891 | 6249 | 6568; |
| 4184 | 2179 | 4554 | 9083 | 2254 | 2435 | 2965 | 5154 | 1209 | 7069 |
| 2916 | 2972 | 9885 | 0275 | 0144 | 8034 | 8122 | 3213 | 7666 | 0230 |
| 5524 | 1341 | 9860 | 6565 | 6981 | 9842 | 0171 | 2284 | 2707 | 3008 |
| 0146 | 5291 | 2354 | 5694 | 0377 | 5336 | 6460 | 9585 | 3415 | 2358 |
| 4920 | 2826 | 5238 | 5402 | 7937 | 1993 | 4332 | 2327 | 6875 | 5230 |
| 7978 | 1947 | , 6380 | 3425 | 7267 | 7285 | 1130 | 7722 | 0164 | 8573 |
| 7453 | 0653 | 3645 | 7497 | 5969 | 8682 | 4191 | 2976 | 0361 | 9334 |
| 1473 | 6938 | 4899 | 5348 | 1641 | 3652 | 0852 | 5296 | 4538 | 4456 |
| 8162 | 8797 | 8000 | 4707 | 1880 | 9660 | 8446 | 1883 | 9768 | 0881 |
| 5645 | 4219 | 0807 | 3301 | 4279 | 4168 | 4305 | 9937 | 3120 | 5547 |
| 2042 | 1192 | 1175 | 8851 | 6432 | 4635 | 5757 | 6656 | 1660 | 5389 |
| 5470 | 7702 | 6958 | 9080 | 5925 | 8519 | 0127 | 9233 | 2452 | 7341 |
| 4045 | 1730 | 6005 | 1704 | 0345 | 3275 | 4738 | 4862 | 2556 | 8333 |
| 5880 | 1257 | 6163 | 4439 | 7276 | 6353 | 6912 | 0731 | 9033 | 5294 |
| 9083 | 4260 | 5277 | 4998 | 4298 | 5204 | 3965, | 4028 | 8936 | 5148 |
| 1762 | 8713 | 1189 | 1090 | 8989 | 7273 | 3213 | 1935 | 9321 | 4820 |
| 2023 | 2589 | 1740 | 0424 | 8924 | 0005 | 1969 | 1636 | 7237 | 1227 |
| 7965 | 3855 | 4765 | 0703 | 1678 | 0841 | 7543 | 0308 | 9732 | 1289 |
| 7690 | 0480 | 8098 | 9629 | 4819 | 7219 | 7241 | 5128 | 3853 | 1921 |
| 9292 | 0426 | 9573 | 4903 | 5916 | 6576 | 8368 | 3270 | 6641 | 0033 |
| 0867 | 1656 | 7016 | 4220 | 2533 | 6345 | 8227 | 1904 | 5138 | 2537 |
| 0505 | 2127 | 8255 | 5276 | 2233 | 3956 | 4118 | 8199 | 6380 | 6340 |
| 6295 | 9795 | 1112 | 5761 | 2575 | 6837 | 3336 | 9322 | 7403 | 8345 |
| 6323 | 2615 | 3410 | 3365' | 1117 | 2417 | 3176 | 2434 | 5240 | 5455 |
| 8672 | 8536 | 2966 | 5773 | 5412 | 8114 | 0930 | 4697 | 6919 | 4569 |
| 1422 | 5507 | 7596 | 0670 | 3013 | 1351 | 3886 | 3268 | 9469 | 2584 |
| 2653 | 1472 | 5113 | 5735 | 1469 | 9545 | 9331 | 5303 | 9914 | 6394 |
| 0438 | 4376 | 3328 | 8649 | 8327 | 0110 | 4549 | 7955 | 5275 | 2890 |
| 2851 | 2157 | 0047 | 7085 | 1129 | 0460 | 6821 | 8323 | 2572 | 8962 |
| 7962 | 2753 | 3077 | 8718 | 7418 | 8004 | 1425 | 3706 | 8822 | 1494 |
| 3837 | 4098 | 0220 | 1217 | 4732 | 0150 | 1637 | 1097 | 1040 | 7372 |
| 8542 | 4126 | 9274 | 2251 | 0607 | 4301 | 8730 | 7690 | 6235 | 3477 |
| 0139 | 0765 | 8039 | 9484 | 2577 | 7859 | 1976 | 0623 | 1418 | 6685 |
| 6687 | 1943 | 4307 | 0579 | 8171 | 8224 | 8641 | 7034 | 3595 | 3875 |
| 6242 | 5582 | 5872 | 3197 | 4919 | 2792 | 5991 | 4058 | 9769 | 1918 |
| 6859 | 9606 | 0522 | 4993 | 0345 | 8958 | 1289 | 8825 | 6941 | 7685 |
| 6590 | 1932 | 6043 | 3623 | 1973 | 4112 | 1795 | 8465 | 2110 | 8045 |
| 3482 | 0478 | 0221 | 6738 | 7323 | 5643 | 4767 | 0106 | 2272 | 9862 |
МИНИСТЕРСТВО ОБЩЕГО И ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
РОССИЙСКОЙ ФЕДЕРАЦИИ
Санкт-Петербургский государственный университет
аэрокосмического приборостроения
СТАТИСТИКА
Выборочные наблюдения
Методические указания к практическим занятиям
Санкт-Петербург
1999
Составитель Н.А. Богородская
Рецензент кандидат экономических наук доцент Л.Г.Фетисова
Методические указания к практическим занятиям предназначены для студентов, изучающих дисциплину "Статистика", обучающихся по направлению и специальности 521500 и 061100 "Менеджмент" и по экономическим специальностям и направлениям 071900, 060400, 060500, 522300 всех форм обучения.
В работе приведены методические указания к решению задач по теме "Выборочные наблюдения" и рассмотрены примеры решения задач для различных видов отбора: механического, собственно-случайного, серийного и типического при повторной и бесповторной выборке единиц из статистической совокупности.
![]()
С Санкт-Петербургский
государственный университет
аэрокосмического
приборостроения, 1999
![]()
Лицензия ЛР №020341 от 07.05.97
Подписано к печати Формат 60ґ84 1/16 Бумага тип. № 3.
Печать офсетная. Усл.печ.л. 1,86 Уч.-изд.л. 2,0 Тираж 100 экз. Заказ №
![]()
Редакционно-издательский отдел
Отдел оперативной полиграфии
СПбГУАП
190000, Санкт-Петербург, ул. Б. Морская, 67
Похожие работы
... будут находиться характеристики генеральной совокупности. 9. Формулы для расчета необходимого объема выборки. 10. Сущность теорем П.Л. Чебышева и А.М. Ляпунова. 11. Распространение результатов выборочного наблюдения на генеральную совокупность. 2.5. Тесты 1. Совокупность, из которой производится отбор единиц для выборочного наблюдения называется: а) выборочной; б) генеральной; ...
... 1. Сущность и виды обобщающих статистических показателей. 2. Абсолютные статистические показатели, их значение в статистике и единицы измерения. 3. Виды относительных величин, техника их расчета и формы выражения. 4. Зависимость между относительными величинами динамики и планового задания. 5. Что выражают относительные величины структуры и координации. 6. Для характеристики каких ...
... Таблица 1 Среднее значение интервала, тыс. грн Фактическое количество предприятий 16 9 20 45 24 16 28 24 32 18 36 12 40 6 Всего 100 Тесты для закрепления материала Тест 1 В статистике критерий Стьюдента обозначается: а) критерий; б) ; в) критерий. Тест 2 Мощность критерия – это: а) вероятность отклонения испытуемой нулевой гипотезы, когда правильною является ...
... учитывается по месту жительства, а не по месту работы [4, 6]. Наблюдение может проводиться собственными силами или организациями, специализирующимися на проведении наблюдений. Проводят наблюдение как органы государственной, так и ведомственной статистики. Рис.2. Органы, которые могут проводить наблюдение [1] В зависимости от особенностей объекта при организации статистического наблюдения ...
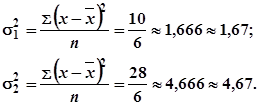

0 комментариев