Навигация
Типический отбор
2.3. Типический отбор
Задача 1. В трех районах 30 тыс. семей. В первом районе - 15 тыс.; во втором - 12 тыс. и в третьем - 3 тыс. семей. Для определения числа детей в семье была проведена 10%-я типическая выборка с отбором единиц пропорционально численности единиц типических групп. Внутри групп применялся метод случайного бесповторного отбора. Результаты выборочного обследования семей в трех районах представлены в табл.2.8
Таблица 2.8
| Номер района | Число семей в районе | Среднее число детей в семье | Среднее квадратическое отклонение |
| 1 2 3 | 15000 12000 3000 | 1,3 1,8 0,8 | 1,2 2,5 0,5 |
С вероятностью 0,997 определить предел, в котором находится среднее число детей в семье в трех районах.
Решение.
Средняя ошибка выборочной средней при типическом бесповторном отборе (см.табл.1.2) определяется следующим образом:
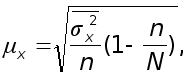
где
![]() – средняя из
групповых
дисперсий
выборочной
средней;
– средняя из
групповых
дисперсий
выборочной
средней;
n – численность выборочной совокупности по всем типическим группам (районам);
N – численность генеральной совокупности (число семей во всех
районах).
Объем выборки в каждой типической группе (районе) nj
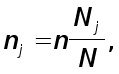
где Nj - число семей в j - м районе;
Число семей, выбранных для обследования в каждом районе при условии, что численность выборочной совокупности n по трем районам равна 3000 семей
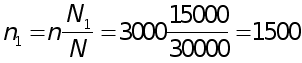 семей;
семей;
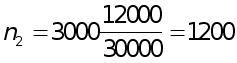 семей;
семей;
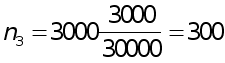 семей.
семей.
Среднее число детей в семье по трем районам в выборочной совокупности (выборочная средняя) с учетом численности отобранных групп
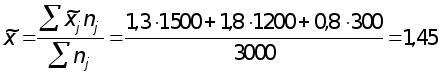 чел.
чел.
Средняя из групповых дисперсий (внутригрупповая дисперсия)
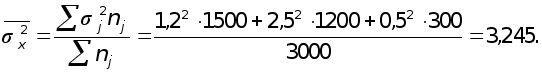
Средняя ошибка выборочной средней при типической выборке (средняя ошибка среднего числа детей в семье)
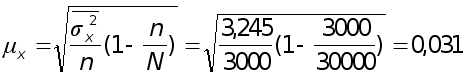 чел.
чел.
Предельная
ошибка средней
с вероятностью
0,997 (гарантийный
коэффициент![]() )
составит
)
составит
![]() чел.
чел.
С вероятностью
0,997 можно утверждать,
что в трех районах
среднее число
детей в семье
находится в
пределах ![]()
Задача 2. Для выявления причин простоев была проведена фотография рабочего дня 10% рабочих четырех различных цехов. Отбор рабочих внутри цехов производился методом случайного бесповторного отбора. В результате анализа выборочных данных была выявлена доля простоев из-за несвоевременного поступления комплектующих изделий (табл.2.9)
Таблица 2.9
| Номер цеха | Число рабочих в выборке, чел. | Удельный вес простоев из-за несвоевременного поступления комплектующих изделий, % |
| 1 2 3 4 | 20 36 14 30 | 5 10 15 2 |
| Итого | 100 | - |
С вероятностью 0,954 определить пределы, в которых находится доля простоев на предприятии из-за несвоевременного поступления комплектующих изделий.
Решение.
Средняя ошибка выборочной доли при типическом бесповторном отборе (см.табл.1.2) определяется следующим образом:
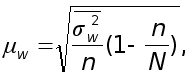
где ![]() – средняя из
групповых
дисперсий
выборочной
доли.
– средняя из
групповых
дисперсий
выборочной
доли.
Средняя выборочная доля простоев из-за несвоевременного поступления комплектующих изделий в четырех цехах
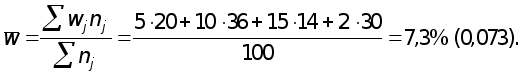
Дисперсия выборочной доли в i -й типической группе определяется по формуле
![]()
Для
первого цеха -
![]()
для
второго -
![]()
для
третьего -
![]()
для
четвертого -
![]()
Средняя из групповых дисперсий выборочной доли
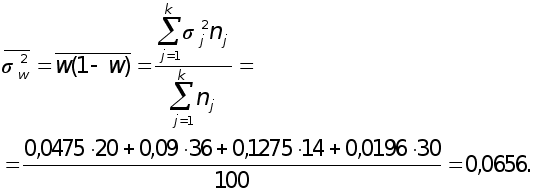
Средняя ошибка выборочной доли
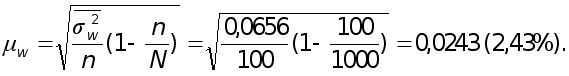
Предельная
ошибка выборочной
доли с вероятностью
0,954 (гарантийный
коэффициент![]() )
)
![]()
С вероятностью 0,954 можно утверждать, что доля простоев из-за несвоевременного поступления комплектующих изделий находится в пределах
![]()
![]()
Задача 3. В трех населенных пунктах 10 тыс. семей. В первом - 5 тыс.; во втором - 1 тыс.; в третьем - 4 тыс. семей. Для определения среднего размера семьи в трех населенных пунктах проектируется типическая выборка со случайным бесповторным отбором внутри типических групп.
Определить объем выборки (количество семей), чтобы с вероятностью 0,987 ошибка выборки при определении среднего размера семьи не превышала 0,5 человека, если на основе предыдущих обследований известно, что дисперсия равна 9.
Решение.
Численность
типической
выборки (при
вероятности
0,987 гарантийный
коэффициент![]() )
)
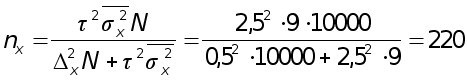 семьи.
семьи.
Задача 4. Для выявления причин простоев 1000 рабочих предприятия необходимо провести типическую выборку по различным цехам.
Определить количество рабочих, которое необходимо обследовать, чтобы с вероятностью 0,997 ошибка выборки (ошибка доли) не превышала 5%, если на основе предыдущих исследований известно, что дисперсия типической выборки равна 0,16.
Решение.
Необходимая
численность
выборки (при
вероятности
0,997 гарантийный
коэффициент![]() )
)
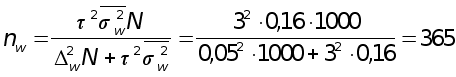 чел.
чел.
Задача 5. На предприятии работает 1000 рабочих, из них в возрасте до 30 лет - 400 человек, свыше 30 лет - 600 человек. Для изучения среднедневной выработки и установления доли мужчин проведена 10%-я типическая выборка с отбором единиц пропорционально численности рабочих по указанным группам (внутри групп применялся случайный метод отбора).
На основе обследования получены следующие данные (табл.2.10):
Таблица 2.10
| Группы рабочих по возрасту, лет | Общая числен-ность рабочих Nj , чел. | Число обследован-ных рабочих nj , чел. | Средне-дневная выра-ботка шт. | Диспер-сия выработ-ки,
| Число мужчин в выборке mj, чел. | Доля мужчин в выборке,
|
| До 30 лет Св. 30 | 400 600 | 40 60 | 25 30 | 81 64 | 32 54 | 0,8 0,9 |
| Итого | 1000 | 100 | - | - | - | - |
Определить:
- с вероятностью 0,954 предельную ошибку выборки и границы, в которых будет находиться среднедневная выработка для всех рабочих предприятия;
- с вероятностью 0,954 пределы удельного веса мужчин в общей численности рабочих предприятия.
Решение.
Средняя ошибка выборочной средней при типическом бесповторном отборе) определяется по формуле
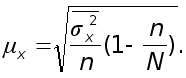
Средняя из групповых дисперсий (внутригрупповая дисперсия)
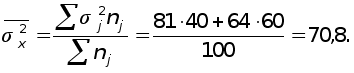
Средняя ошибка среднедневной выработки рабочих в выборке (средняя
ошибка выборочной средней)
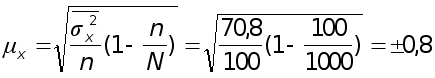 шт.
шт.
Предельная
ошибка средней
с вероятностью
0,954 (гарантийный
коэффициент![]() )
составит
)
составит
![]() шт.
шт.
Для определения возможных пределов среднедневной выработки всех рабочих предприятия рассчитывается среднедневная выработка в выборочной совокупности по средней арифметической взвешенной
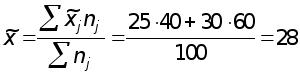 шт.
шт.
С вероятностью 0,954 можно утверждать, что среднедневная выработка всех рабочих предприятия находится в пределах
![]()
Средняя ошибка выборочной доли при типическом бесповторном отборе определяется по формуле
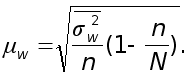
Средняя
из групповых
дисперсий
выборочной
доли. ![]() рассчитывается
следующим
образом:
рассчитывается
следующим
образом:
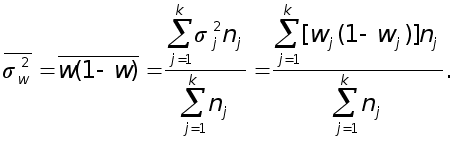
Расчет представлен в табл.2.11
Таблица 2.11
| Группы рабочих по возрасту, лет | Число рабочих nj, чел. | Доля мужчин
| Доля женщин
| Дисперсия доли
| Взвешенный показатель дисперсии
|
| До 30 лет Свыше 30 | 40 60 | 0,8 0,9 | 0,2 0,1 | 0,16 0,09 | 6,4 5,4 |
| Итого | 100 | 11,8 |
Тогда
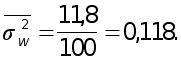
Средняя ошибка репрезентативности для выборочной доли
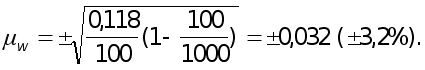
Предельная
ошибка выборочной
доли с вероятностью
0,954 (гарантийный
коэффициент ![]() )
)
![]()
Для определения пределов доли мужчин рассчитывается средняя доля для выборочной совокупности
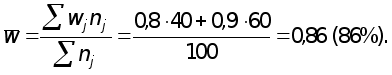
С вероятностью 0,954 можно утверждать, что доля мужчин на предприятии находится в пределах
![]()
![]()
Библиографический список
1. Богородская Н.А. Статистика. Методы анализа статистической
информации: Текст лекций / СПбГААП. СПб., 1997. 80 с.
2. Ефимова М.Р., Петрова Е.В., Румянцев В.Н. Общая теория статистики.
Учебник. М.: ИНФРА-М, 1998. 416 с.
3. Статистика: Курс лекций / Л.П.Харченко, В.Г.Долженкова, В.Г. Ионин и
др.; Под ред. В.Г.Ионина. Новосибирск: Изд-во НГАЭиУ, 1996. 310 с.
4. Общая теория статистики: Статистическая методология в изучении
коммерческой деятельности. Учебник /А.И.Харламов, О.Э.Башина,
В.Т.Бабурин и др.; Под ред. А.А.Спирина, О.Э.Башиной. М.: Финансы
статистика, 1994. 296 с.
5. Гусаров В.М. Теория статистики. М.: Аудит, 1998. 247 с.
6. Елисеева И.И., Юзбашев М.М. Общая теория статистики. М.: Финансы и
статистика, 1998. 367 с.
7. Теория статистики. Учебник / Под ред. Р.А.Шмойловой. М.: Финансы и
статистика, 1998. 576 с.
8. Практикум по теории статистики: Учеб. пособие / Под ред.
Р.А.Шмойловой. М.: Финансы и статистика, 1998. 416 с.
9. Громыко Г.Л. Общая теория статистики: Практикум. М.: ИНФРА-М,
1999. 139 с.
10. Сборник задач по общей теории статистики: Учеб. пособие для
студентов вузов, обучающихся по специальности “Статистика” /
В.Е.Овсиенко, Н.В.Голованова, Ю.Г.Королев и др. 2-е изд., перераб. и
доп. М.: Финансы и статистика, 1986. 191 с.
Содержание
1. МЕТОДИЧЕСКИЕ УКАЗАНИЯ К РЕШЕНИЮ ЗАДАЧ ПО ТЕМЕ
"ВЫБОРОЧНЫЕ НАБЛЮДЕНИЯ" . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1
1.1. Выборочное исследование . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1
1.2. Виды отбора при выборочном наблюдении . . . . . . . . . . . . . . . . 1
1.3. Ошибки выборочного отбора . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3
1.3.1. Ошибка выборочной доли . . . . . . . . . . . . . . . . . . . . . . . . . . 3
4.3.2. Ошибка выборочной средней . . . . . . . . . . . . . . . . . . . . . . . 7
1.4. Объем выборки . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . 8
2. ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . 10
2.1. Механический и собственно-случайный отбор . . . . . . . . . . . . . . . . 10
2.2. Серийный отбор . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . 19
2.3. Типический отбор . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . 25
Библиографический список . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Похожие работы
... будут находиться характеристики генеральной совокупности. 9. Формулы для расчета необходимого объема выборки. 10. Сущность теорем П.Л. Чебышева и А.М. Ляпунова. 11. Распространение результатов выборочного наблюдения на генеральную совокупность. 2.5. Тесты 1. Совокупность, из которой производится отбор единиц для выборочного наблюдения называется: а) выборочной; б) генеральной; ...
... 1. Сущность и виды обобщающих статистических показателей. 2. Абсолютные статистические показатели, их значение в статистике и единицы измерения. 3. Виды относительных величин, техника их расчета и формы выражения. 4. Зависимость между относительными величинами динамики и планового задания. 5. Что выражают относительные величины структуры и координации. 6. Для характеристики каких ...
... Таблица 1 Среднее значение интервала, тыс. грн Фактическое количество предприятий 16 9 20 45 24 16 28 24 32 18 36 12 40 6 Всего 100 Тесты для закрепления материала Тест 1 В статистике критерий Стьюдента обозначается: а) критерий; б) ; в) критерий. Тест 2 Мощность критерия – это: а) вероятность отклонения испытуемой нулевой гипотезы, когда правильною является ...
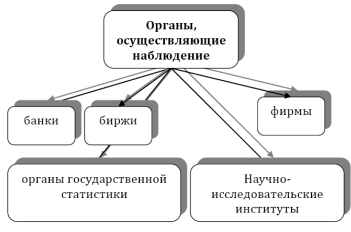
... учитывается по месту жительства, а не по месту работы [4, 6]. Наблюдение может проводиться собственными силами или организациями, специализирующимися на проведении наблюдений. Проводят наблюдение как органы государственной, так и ведомственной статистики. Рис.2. Органы, которые могут проводить наблюдение [1] В зависимости от особенностей объекта при организации статистического наблюдения ...
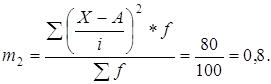
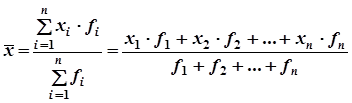
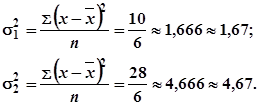

0 комментариев