Навигация
Ошибка выборочной средней
1.3.2. Ошибка выборочной средней
Ошибка
выборочной
средней представляет
собой расхождение
(разность) между
выборочной
средней
![]() и генеральной
средней
и генеральной
средней
![]() ,
возникающее
вследствие
несплошного
выборочного
характера
наблюдения.
Величина ошибки
выборочной
средней определяется
как предел
отклонения
,
возникающее
вследствие
несплошного
выборочного
характера
наблюдения.
Величина ошибки
выборочной
средней определяется
как предел
отклонения
![]() от
от
![]() ,
гарантируемый
с заданной
вероятностью:
,
гарантируемый
с заданной
вероятностью:
![]()
где ![]() – средняя ошибка
выборочной
средней.
– средняя ошибка
выборочной
средней.
При повторном отборе средняя ошибка определяется следующим образом:
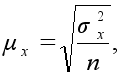
где
![]() – средняя величина
дисперсии
количественного
признака
– средняя величина
дисперсии
количественного
признака
![]() ,
которая рассчитывается
по формуле
средней арифметической
невзвешенной
,
которая рассчитывается
по формуле
средней арифметической
невзвешенной
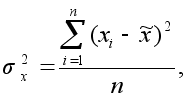
или средней арифметической взвешенной
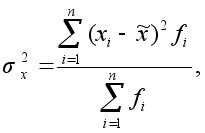
где fi – статистический вес.
Формулы расчета средней ошибки выборочной средней для различных способов отбора выборочной совокупности приведены в табл.1.2.
Межсерийная
дисперсия
выборочных
средних
![]() и средняя из
выборочных
дисперсий
типических
групп
и средняя из
выборочных
дисперсий
типических
групп ![]() вычисляются
следующим
образом:
вычисляются
следующим
образом:
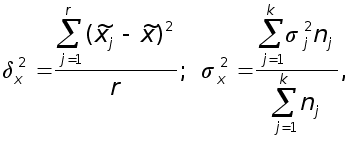
где
![]() – среднее значение
показателя в j
- й серии;
– среднее значение
показателя в j
- й серии;
![]() –
дисперсия
признака
x в
j
- й типической
группе;
–
дисперсия
признака
x в
j
- й типической
группе;
nj – число единиц в j - й типической группе.
Предельная ошибка выражается следующим образом:
![]()
и зависит от вариации изучаемого признака в генеральной совокупности, объема и доли выборки, способа отбора единиц из генеральной совокупности и от величины вероятности, с которой гарантируются результаты выборочного наблюдения.
Средняя
величина
количественного
признака в
генеральной
совокупности
определяется
с учетом предельной
ошибки выборочной
средней
![]()
4.4. Объем выборки
Определение необходимого объема выборки n основывается на формулах предельных ошибок выборочной доли и выборочной средней. Например, для повторного отбора предельные ошибки равны
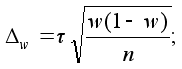
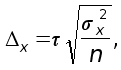
отсюда объемы выборок для расчета выборочной доли nw и выборочной средней nx следующие:
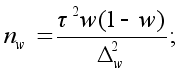
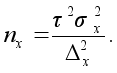
Аналогичным образом определяются объемы выборок при различных способах отбора выборочной совокупности. Для серийного отбора определяется число отобранных серий. Формулы расчета приведены в табл.1.3.
Таблица 1.3
Формулы расчета объема выборки
Метод отбора выборки | Объем выборки или число серий для определения | |
выборочной доли | выборочной средней | |
Механический и собственно–случайный повторный |
|
|
| Механический и собственно–случайный бесповторный |
|
|
Серийный при бесповторном отборе серий |
|
|
| Типический при повторном случайном отборе внутри групп |
|
|
| Типический при бесповторном случайном отборе внутри групп |
|
|
где nw, nx – объемы выборок соответственно для определения ошибок выборочной доли и выборочной средней;
rw, rx – число отобранных серий соответственно для определения ошибок выборочной доли и выборочной средней;
![]() – предельные
ошибки соответственно
выборочной
доли и выборочной
средней.
– предельные
ошибки соответственно
выборочной
доли и выборочной
средней.
Похожие работы
... будут находиться характеристики генеральной совокупности. 9. Формулы для расчета необходимого объема выборки. 10. Сущность теорем П.Л. Чебышева и А.М. Ляпунова. 11. Распространение результатов выборочного наблюдения на генеральную совокупность. 2.5. Тесты 1. Совокупность, из которой производится отбор единиц для выборочного наблюдения называется: а) выборочной; б) генеральной; ...
... 1. Сущность и виды обобщающих статистических показателей. 2. Абсолютные статистические показатели, их значение в статистике и единицы измерения. 3. Виды относительных величин, техника их расчета и формы выражения. 4. Зависимость между относительными величинами динамики и планового задания. 5. Что выражают относительные величины структуры и координации. 6. Для характеристики каких ...
... Таблица 1 Среднее значение интервала, тыс. грн Фактическое количество предприятий 16 9 20 45 24 16 28 24 32 18 36 12 40 6 Всего 100 Тесты для закрепления материала Тест 1 В статистике критерий Стьюдента обозначается: а) критерий; б) ; в) критерий. Тест 2 Мощность критерия – это: а) вероятность отклонения испытуемой нулевой гипотезы, когда правильною является ...
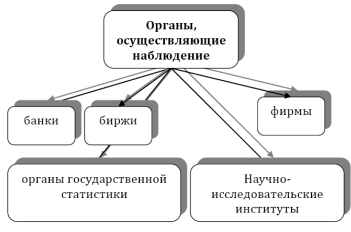
... учитывается по месту жительства, а не по месту работы [4, 6]. Наблюдение может проводиться собственными силами или организациями, специализирующимися на проведении наблюдений. Проводят наблюдение как органы государственной, так и ведомственной статистики. Рис.2. Органы, которые могут проводить наблюдение [1] В зависимости от особенностей объекта при организации статистического наблюдения ...
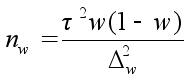
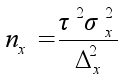
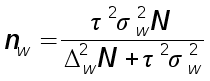
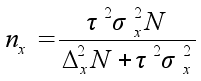
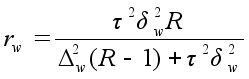
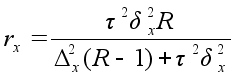
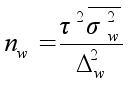
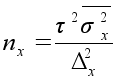

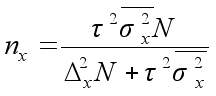
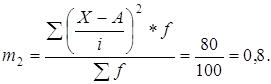
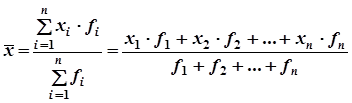
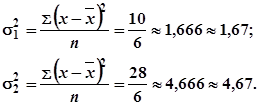

0 комментариев