Навигация
Ошибки выборочного отбора
1.3. Ошибки выборочного отбора
Расхождение между значениями изучаемого признака выборочной и генеральной совокупностей является ошибкой репрезентативности (представи–тельности). Она может быть случайной и систематической. Случайная возникает в силу того, что выборочное статистическое наблюдение является несплошным наблюдением, и выборка недостаточно точно воспроизводит (репрезентирует) генеральную совокупность. При определении величины репрезентативной ошибки предполагается, что ошибка регистрации равна нулю. Определение ошибки производится по формулам ошибки выборочной доли и ошибки выборочной средней.
1.3.1. Ошибка выборочной доли
Выборочная доля представляет собой отношение числа единиц, обладающих данным признаком или данным его значением ( m ), к общему числу единиц выборочной совокупности ( n )
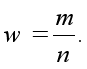
(Эту статистическую характеристику не следует путать с долей выборки, являющейся отношением числа единиц выборочной совокупности к числу единиц генеральной совокупности).
Ошибка выборочной доли представляет собой расхождение (разность) между долей в выборочной совокупности ( w ) и долей в генеральной совокупности ( p ), возникающее вследствие несплошного характера наблюдения. Величина ошибки выборочной доли определяется как предел отклонения w от p , гарантируемый с заданной вероятностью:
![]()
где
![]() – гарантийный
коэффициент,
зависящий от
вероятности
– гарантийный
коэффициент,
зависящий от
вероятности ![]() , с которой
гарантируется
невыход разности w –p за пределы
, с которой
гарантируется
невыход разности w –p за пределы
![]() ;
;
![]() – средняя ошибка
выборочной
доли.
– средняя ошибка
выборочной
доли.
Значения
гарантийного
коэффициента
![]() и соответствующие
им вероятности
и соответствующие
им вероятности ![]() приведены
в табл.1.1.
Обычно вероятность
принимается
равной 0,9545 или
0,9973, а
приведены
в табл.1.1.
Обычно вероятность
принимается
равной 0,9545 или
0,9973, а ![]() при этом равно
соответственно
2 и 3.
при этом равно
соответственно
2 и 3.
Значения средней ошибки выборки определяются по формуле
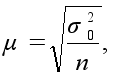
где ![]() – дисперсия
в генеральной
совокупности.
– дисперсия
в генеральной
совокупности.
Между дисперсиями в генеральной и выборочной совокупностях существует следующее соотношение:
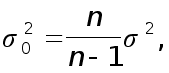
где
![]() –
дисперсия в
выборке.
–
дисперсия в
выборке.
Таблица 1.1
Значения
гарантийного
коэффициента
![]()
|
|
|
|
|
|
|
| 1,00 1,10 1,20 1,30 1,40 1,50 1,60 | 0,6827 0,7287 0,7699 0,8064 0,8385 0,8664 0,8904 | 1,70 1,80 1,90 2,00 2,10 2,20 2,30 | 0,9109 0,9281 0,9426 0,9545 0,9643 0,9722 0,9786 | 2,40 2,50 2,60 2,70 2,80 2,90 3,00 | 0,9836 0,9876 0,9907 0,9931 0,9949 0,9963 0,9973 |
Если n достаточно
велико, то
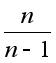 близко к единице
и дисперсию
в генеральной
совокупности
можно заменить
на дисперсию
в выборке.
близко к единице
и дисперсию
в генеральной
совокупности
можно заменить
на дисперсию
в выборке.
Средняя ошибка выборочной доли определяется по формуле
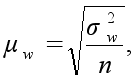
где
![]() – дисперсия
выборочной
доли.
– дисперсия
выборочной
доли.
Для показателя доли альтернативного признака (выборочной доли) дисперсия определяется по формуле
![]()
Приведенная формула средней ошибки выборочной доли применяется при повторном отборе.
При бесповторном
отборе численность
генеральной
совокупности
сокращается,
поэтому дисперсия
умножается
на коэффициент
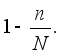 Формулы расчета
средних ошибок
выборочной
доли для различных
способов отбора
единиц из генеральной
совокупности
приведены в
табл. 1.2.
Формулы расчета
средних ошибок
выборочной
доли для различных
способов отбора
единиц из генеральной
совокупности
приведены в
табл. 1.2.
Таблица 1.2
Формулы расчета средних ошибок выборочной доли
и выборочной средней
| Метод отбора выборки | Средняя ошибка | |
| выборочной доли | выборочной средней | |
| Механический и собственно–случайный повторный |
|
|
Механический и собственно–случайный бесповторный |
|
|
| Серийный при бесповторном отборе серий |
|
|
| Типический при повторном случайном отборе внутри групп |
|
|
| Типический при бесповторном случайном отборе внутри групп |
|
|
где N – численность генеральной совокупности;
![]() – межсерийная
дисперсия
выборочной
доли;
– межсерийная
дисперсия
выборочной
доли;
r – число отобранных серий;
R – число серий в генеральной совокупности;
![]() – средняя
из групповых
дисперсий
выборочной
доли;
– средняя
из групповых
дисперсий
выборочной
доли;
![]() – дисперсия
признака x ;
– дисперсия
признака x ;
![]() – межсерийная
дисперсия
выборочных
средних;
– межсерийная
дисперсия
выборочных
средних;
![]() – средняя
из групповых
дисперсий
выборочной
средней.
– средняя
из групповых
дисперсий
выборочной
средней.
Дисперсии в формулах расчета средних ошибок выборочной доли в табл.1.2 определяется следующим образом:
– межсерийная дисперсия выборочной доли
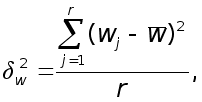
где wj – выборочная доля в j -й серии;
![]() – средняя
величина доли
во всех сериях;
– средняя
величина доли
во всех сериях;
– средняя из групповых дисперсий
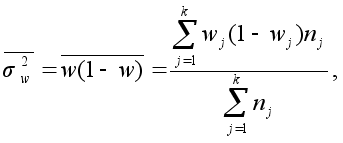
где wj – выборочная доля в j -й типической группе;
nj – число единиц в j -й типической группе;
k – число типических групп.
Предельное значение ошибки выборочной доли определяется по следующей формуле:
![]()
Величина
средней ошибки
выборочной
доли
![]() зависит
от доли изучаемого
признака в
генеральной
совокупности,
числа наблюдений
и способа отбора
единиц из генеральной
совокупности
для наблюдения,
а величина
предельной
ошибки
зависит
от доли изучаемого
признака в
генеральной
совокупности,
числа наблюдений
и способа отбора
единиц из генеральной
совокупности
для наблюдения,
а величина
предельной
ошибки
![]() зависит еще
и от величины
вероятности
зависит еще
и от величины
вероятности
![]() ,
с которой
гарантируются
результаты
выборочного
наблюдения.
,
с которой
гарантируются
результаты
выборочного
наблюдения.
Распространение
выборочных
данных на генеральную
совокупность
производится
с учетом доверительных
интервалов.
Доля альтернативного
признака в
генеральной
совокупности
равна![]()
Похожие работы
... будут находиться характеристики генеральной совокупности. 9. Формулы для расчета необходимого объема выборки. 10. Сущность теорем П.Л. Чебышева и А.М. Ляпунова. 11. Распространение результатов выборочного наблюдения на генеральную совокупность. 2.5. Тесты 1. Совокупность, из которой производится отбор единиц для выборочного наблюдения называется: а) выборочной; б) генеральной; ...
... 1. Сущность и виды обобщающих статистических показателей. 2. Абсолютные статистические показатели, их значение в статистике и единицы измерения. 3. Виды относительных величин, техника их расчета и формы выражения. 4. Зависимость между относительными величинами динамики и планового задания. 5. Что выражают относительные величины структуры и координации. 6. Для характеристики каких ...
... Таблица 1 Среднее значение интервала, тыс. грн Фактическое количество предприятий 16 9 20 45 24 16 28 24 32 18 36 12 40 6 Всего 100 Тесты для закрепления материала Тест 1 В статистике критерий Стьюдента обозначается: а) критерий; б) ; в) критерий. Тест 2 Мощность критерия – это: а) вероятность отклонения испытуемой нулевой гипотезы, когда правильною является ...
... учитывается по месту жительства, а не по месту работы [4, 6]. Наблюдение может проводиться собственными силами или организациями, специализирующимися на проведении наблюдений. Проводят наблюдение как органы государственной, так и ведомственной статистики. Рис.2. Органы, которые могут проводить наблюдение [1] В зависимости от особенностей объекта при организации статистического наблюдения ...
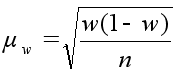
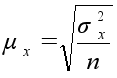
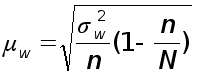
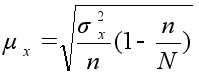
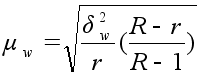
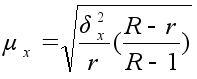
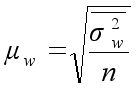
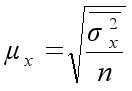
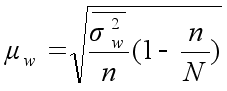
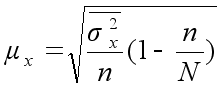
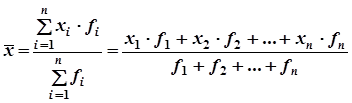

0 комментариев