Навигация
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
2. ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
2.1. Механический и собственно-случайный отбор
Задача 1. В районе А проживает 2500 семей. Для проведения обследования выбрано 50 семей методом механического (или собственно-случайного) бесповторного отбора. В результате обследования получены следующие данные о количестве детей в семье:
Таблица 2.1
| Число детей в семье | 0 | 1 | 2 | 3 | 4 | 5 |
| Количество семей | 10 | 20 | 12 | 4 | 2 | 2 |
Определить среднюю ошибку выборочной средней количества детей в семье и с вероятностью 0,997 пределы, в которых находится среднее количество детей в семье в районе А.
Решение.
Средняя ошибка выборочной средней определяется по следующей формуле (см.табл.1.2):
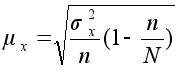 ,
,
где n - численность выборки;
N - численность генеральной совокупности;
![]() - дисперсия
признака x .
- дисперсия
признака x .
Дисперсия
![]() определяется
по формуле
определяется
по формуле
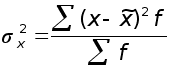 , а среднее
выборочное
значение
, а среднее
выборочное
значение
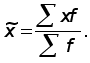
Расчет среднего и дисперсии числа детей в семье в выборочной совокупности приведены в табл.2.2.
Таблица 2.2
| Число детей в семье
| Количество семей |
|
|
|
|
| 0 1 2 3 4 5 | 10 20 12 4 2 2 | 0 20 24 12 8 10 | -1,48 -0,48 +0,52 +1,52 +2,52 +3,52 | -14,8 - 9,6 +6,24 +6,08 +5,04 +7,04 | 21,9040 4,6080 3,2448 9,2416 12,7008 24,7808 |
| Итого | 50 | 74 | - | 0 | 76,4800 |
Среднее число детей в семье
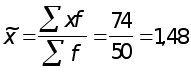 чел.
чел.
Дисперсия числа детей в семье
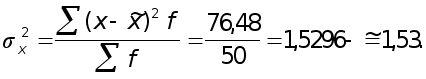
Средняя ошибка числа детей в выборке составит
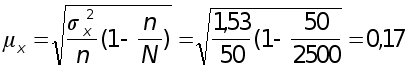 чел.
чел.
Значению
вероятности
0,997 соответствует
значение гарантийного
коэффициента
![]() Тогда предельная
ошибка выборочной
средней
Тогда предельная
ошибка выборочной
средней
![]() чел.
чел.
Значение генеральной средней определяется
![]()
Пределы, в которых находится среднее число детей в семье в районе А:
![]()
![]()
С вероятностью 0,997 можно утверждать, что число детей в семьях района А колеблется от 0,99 до 2,01 человека ( от 1 до 2 человек).
Задача 2. Методом собственно-случайного (или механического) повторного отбора было взято для проверки на вес 200 штук деталей. В результате проверки был установлен средний вес деталей 30 г при среднем квадратическом отклонении 4 г.
С вероятностью 0,954 определить пределы, в которых находится средний вес деталей в генеральной совокупности.
Решение.
Средняя ошибка среднего веса деталей в выборке (выборочной средней)
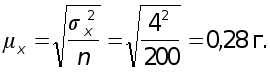
Предельная
ошибка выборочной
средней с
вероятностью
0,954 (гарантийный
коэффициент![]() )
составит
)
составит
![]()
Верхняя граница генеральной средней
![]()
Нижняя граница генеральной средней
![]()
С вероятностью 0,954 можно утверждать, что средний вес детали колеблется в пределах
![]()
Задача 3. Методом собственно-случайного (или механического) бесповторного отбора из общей численности работников предприятия (5 тыс.чел.) было отобрано 500 работников. Установлено, что 20% работников в выборке старше 60 лет.
Определить с вероятностью 0,683 пределы, в которых находится доля работников предприятия в возрасте старше 60 лет.
Решение.
Средняя ошибка выборочной доли работников старше 60 лет определяется следующим образом (см.табл.1.2)
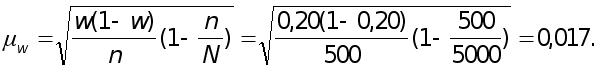
С вероятностью
0,683 (гарантийный
коэффициент![]() )
предельная
ошибка выборочной
доли работников
старше 60-ти лет
составит
)
предельная
ошибка выборочной
доли работников
старше 60-ти лет
составит
![]()
Верхняя граница генеральной доли
![]()
Нижняя граница генеральной доли
![]()
С вероятностью 0,683 можно утверждать, что доля работников в возрасте старше 60 лет на предприятии колеблется от 18,3% до 21,7%.
![]()
Задача 4. При обследовании 100 изделий, отобранных из партии методом механического (или собственно-случайного) повторного отбора, 10 изделий оказались дефектными.
Определить с вероятностью 0,866 пределы, в которых находится доля дефектных изделий в партии.
Решение.
Для дефектной продукции в выборочной совокупности
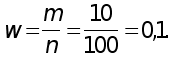
Средняя ошибка выборочной доли дефектных изделий равна (см.табл.1.2)
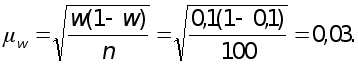
Предельная
ошибка выборочной
доли с вероятностью
0.866 (гарантийный
коэффициент![]() )
составит
)
составит
![]()
С вероятностью 0,866 можно утверждать, что доля дефектной продукции в партии колеблется от 5,5% до 14,5%.
![]()
Задача 5. В районе А проживает 2000 семей. Предполагается определить средний размер семьи в районе по выборке, взятой методом механического (или собственно-случайного) бесповторного отбора. При этом с вероятностью 0,997 ошибка среднего размера семьи в выборке (выборочной средней) не должна превышать 0,8 человека при среднем квадратическом отклонении в размере семьи 2 человека.
Определить необходимую численность выборки для определения среднего размера семьи в районе.
Решение.
Необходимая
численность
выборки (см.табл.1.3)
при вероятности
0,997 (гарантийный
коэффициент![]() )
определяется
следующим
образом:
)
определяется
следующим
образом:
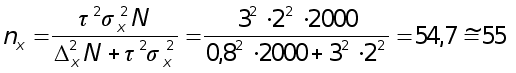 семей.
семей.
Проверка. Средняя ошибка среднего размера семьи составляет
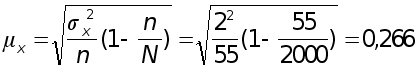 чел.
чел.
Предельная
ошибка выборочной
средней при
вероятности
0,997 (![]() )
)
![]() чел. не превышает
заданной ошибки
0,8 чел.
чел. не превышает
заданной ошибки
0,8 чел.
Задача 6. Для определения средней длины детали необходимо провести выборочное обследование методом случайного (или механического) повторного отбора.
Определить, какое количество деталей необходимо отобрать (числен-ность выборки), чтобы ошибка выборки (ошибка выборочной средней) не превышала 2 мм с вероятностью 0,988 при среднем квадратическом отклонении 8 мм.
Решение.
Необходимая
численность
выборки в случае
повторного
собственно-случайного
(или механического)
отбора (см.табл.1.3)
при вероятности
0,997 (гарантийный
коэффициент![]() )
определяется
следующим
образом:
)
определяется
следующим
образом:
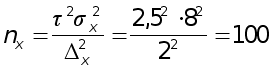 деталей.
деталей.
Проверка. Средняя ошибка средней длины детали составляет
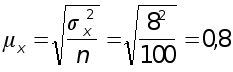 мм.
мм.
Предельная
ошибка выборочной
средней при
вероятности
0,988 (![]() ) составляет
) составляет![]() мм, что соответствует
условию задачи.
мм, что соответствует
условию задачи.
Задача 7. В городе А имеется 10 тыс.семей. С использованием метода выборочных наблюдений предполагается определить долю семей с числом детей три и более.
Определить численность выборки, чтобы при механическом (или собственно-случайном) отборе с вероятностью 0,954 ошибка выборки (доли семей с числом детей три и более) не превышала 0,02, если на основе предыдущих обследований известно, что дисперсия равна 0,2.
Решение.
Необходимая
численность
выборки для
определения
доли семей с
числом детей
три и более
(см.табл.1.3) при
вероятности
0,954 (гарантийный
коэффициент![]() )
определяется
)
определяется
для бесповторного отбора
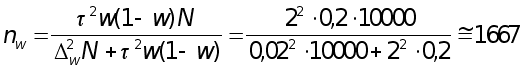 семей;
семей;
для повторного отбора
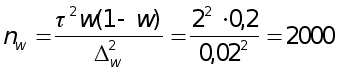 семей.
семей.
Задача 8. Для изучения оснащения 500 предприятий основными производственными фондами было проведено 10%-е выборочное обследование методом собственно-случайного (или механического) отбора, в результате которого получены следующие данные о распределении предприятий по стоимости основных производственных фондов:
Таблица 2.3
| Среднегодовая стоимость основных производственных фондов, млн р. | До 20 | 20-40 | 40-60 | Свыше 60 | Итого: |
Число предприятий | 5 | 12 | 23 | 10 | 50 |
Определить:
- с вероятностью 0,997 предельную ошибку выборочной средней и границы, в которых будет находиться среднегодовая стоимость основных производственных фондов всех предприятий генеральной совокупности;
- с вероятностью 0,954 предельную ошибку выборки при определении доли и границы, в которых будет находиться удельный вес предприятий со стоимостью основных производственных фондов свыше 40 млн р.;
- объемы выборочной совокупности при условии, что:
предельная ошибка выборки при определении среднегодовой стоимости основных производственных фондов с вероятностью 0,997 была бы не более 5 млн р.;
предельная ошибка доли предприятий со стоимостью основных производственных фондов свыше 40 млн р. с вероятностью 0,954 была бы не более 15%.
Решение.
Для определения
границ генеральной
средней необходимо
вычислить
среднюю выборочную
![]() и дисперсию
и дисперсию
![]() , расчет которых
приведен в
табл.2.3.
, расчет которых
приведен в
табл.2.3.
Тогда
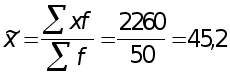 млн р.;
млн р.;
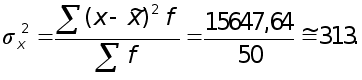
Таблица 2.4
| Среднегодовая стоимость основных производственных фондов, млн р. | Число пред-прия-тий
| Сере-дина интер-вала, млн р.
|
|
|
|
|
| До 20 20 - 40 40 - 60 Свыше 60 | 5 12 23 10 | 10 30 50 70 | 50 360 1150 700 | -35,2 -15,2 4,8 24,8 | -176,0 -182,4 110,4 248,0 | 6195,20 2772,48 529,92 6150,04 |
| Итого | 50 | - | 2260 | - | 0 | 15647,64 |
Для упрощения расчета средней и дисперсии можно использовать способ моментов.
При следующих
исходных данных: N
=500; n =50; ![]() средняя
ошибка выборки
при определении
среднегодовой
стоимости
основных фондов
составит:
средняя
ошибка выборки
при определении
среднегодовой
стоимости
основных фондов
составит:
при повторном отборе
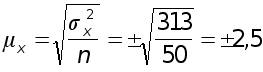 млн р.;
млн р.;
при бесповторном отборе
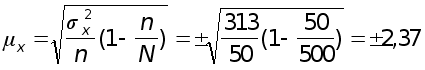 млн.р.
млн.р.
При определении среднегодовой стоимости основных производственных фондов в среднем на одно предприятие в выборочной совокупности средняя ошибка выборки (ошибка репрезентативности) при повторном отборе составляет 2,5 млн р., при бесповторном - 2,37.
Предельная
ошибка выборочной
средней с
вероятностью
0,997 (гарантийный
коэффициент![]() )
составит
)
составит
при повторном отборе
![]() млн р.
млн р.
при бесповторном отборе
![]() млн р.
млн р.
Значение генеральной средней определяется
![]()
Пределы, в которых находится среднее число детей в семье в районе А:
![]()
Среднегодовая стоимость основных производственных фондов в среднем на одно предприятие генеральной совокупности находится в следующих пределах:
при повторном отборе
![]() млн.р или
млн.р или ![]() ;
;
при бесповторном отборе
![]() млн.р или
млн.р или ![]() .
.
Эти границы можно гарантировать с вероятностью 0,997.
Вычисление пределов при установлении доли осуществляется аналогично нахождению пределов для средней величины
![]()
![]()
где p - доля единиц в генеральной совокупности, обладающих данным признаком.
Доля предприятий в выборочной совокупности со среднегодовой стоимостью основных производственных фондов свыше 40 млн р. составляет
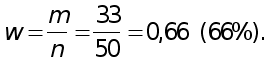
Предельная
ошибка доли
с вероятностью
0,954 (гарантийный
коэффициент![]() ):
):
при повторном отборе
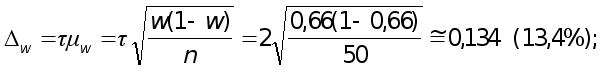
при бесповторном отборе
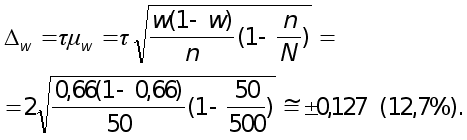
С вероятностью 0,954 доля предприятий со среднегодовой стоимостью основных производственных фондов свыше 40 млн р. в генеральной совокупности находится в пределах:
при повторном отборе
![]() или
или ![]() ;
;
при бесповторном отборе
![]() или
или ![]()
При бесповторном отборе ошибка выборки меньше, чем при тех же условиях при повторной выборке.
Объем выборки
для расчета
ошибки средней
при N
=500; n =50; ![]() ;
;
![]() млн
р. с вероятностью
0,997 (гарантийный
коэффициент
млн
р. с вероятностью
0,997 (гарантийный
коэффициент![]() )
)
при повторном отборе
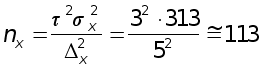 предпр.;
предпр.;
при бесповторном отборе
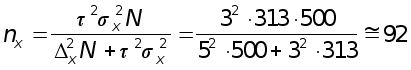 предпр.
предпр.
Объем выборки
для расчета
ошибки доли
при N
=500; n =50; ![]() ;
;
![]() с вероятностью
0,954 (гарантийный
коэффициент
с вероятностью
0,954 (гарантийный
коэффициент![]() )
)
при повторном отборе
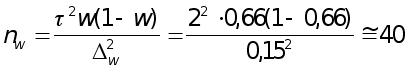 предпр.;
предпр.;
при бесповторном отборе
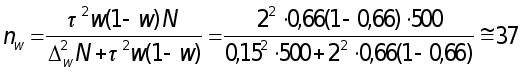 предпр.
предпр.
Похожие работы
... будут находиться характеристики генеральной совокупности. 9. Формулы для расчета необходимого объема выборки. 10. Сущность теорем П.Л. Чебышева и А.М. Ляпунова. 11. Распространение результатов выборочного наблюдения на генеральную совокупность. 2.5. Тесты 1. Совокупность, из которой производится отбор единиц для выборочного наблюдения называется: а) выборочной; б) генеральной; ...
... 1. Сущность и виды обобщающих статистических показателей. 2. Абсолютные статистические показатели, их значение в статистике и единицы измерения. 3. Виды относительных величин, техника их расчета и формы выражения. 4. Зависимость между относительными величинами динамики и планового задания. 5. Что выражают относительные величины структуры и координации. 6. Для характеристики каких ...
... Таблица 1 Среднее значение интервала, тыс. грн Фактическое количество предприятий 16 9 20 45 24 16 28 24 32 18 36 12 40 6 Всего 100 Тесты для закрепления материала Тест 1 В статистике критерий Стьюдента обозначается: а) критерий; б) ; в) критерий. Тест 2 Мощность критерия – это: а) вероятность отклонения испытуемой нулевой гипотезы, когда правильною является ...
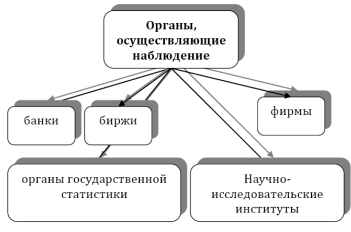
... учитывается по месту жительства, а не по месту работы [4, 6]. Наблюдение может проводиться собственными силами или организациями, специализирующимися на проведении наблюдений. Проводят наблюдение как органы государственной, так и ведомственной статистики. Рис.2. Органы, которые могут проводить наблюдение [1] В зависимости от особенностей объекта при организации статистического наблюдения ...
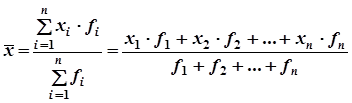
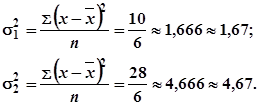

0 комментариев