Классификация элементов симметрии молекулы
Групповые постулаты
Определение группы
Классы смежности и классы сопряженных элементов
Факторизация групп
База (базис) и размерность векторного пространства
Эвклидовы и унитарные пространства
Представления групп
Представления групп и модули
Представление алгебр и модули
Таблицы характеров неприводимых представлений
Найти всевозможные линейно независимые общие правые собственные векторы
Операторы проектирования
Разложение представления в прямую сумму неприводимых представлений с помощью оператора Вигнера
Навигация
Теория симметрии молекул
Теория симметрии молекул
74215
знаков
5
таблиц
9
изображений
Министерство общего и профессионального образования РФ
Дипломная работа
«Теория симметрии молекул»
Содержание
Введение
Глава 1 Элементы теории групп симметрии молекул
1.1 Операции симметрии молекул
1.2 Групповые постулаты
1.3 Классы смежности и классы сопряженных элементов
1.4 Факторизация групп
Глава 2 Введение в теорию представлений групп симметрии молекул
2.1 Векторные (линейные) пространства
2.2 Эвклидовы и унитарные пространства
2.3 Матрицы
2.4 Представления групп
2.5 Характеры представлений
2.6 Операторы проектирования
Заключение
Список использованной литературы
Введение
Понятие симметрии играет важную роль во всех естественных науках. Свойствами симметрии обладают структуры многих молекул, ионов, образуемых ими реагирующих систем.
Математической основой теории симметрии является теория групп. Понятие группы – предмет теории групп.
Множество G с бинарной операцией называется группой, если:
1. Операция ассоциативна, т. е. 
для любых a, b, c из G.
2. Операция гарантирует единицу, т. е. в G существует такой элемент е – он называется единицей, - что 
для любого а из G.
3. Операция гарантирует обратные элементы, т. е. для любого а из G существует в G такой элемент а-1 – он называется обратным к а, - что 
.
В теории молекулярной симметрии понятие представления группы играет центральную роль. Учитывая это, дадим определение представления группы, используя различные математические объекты, представляющие группу.
Представлением группы, действующим в n-мерном векторном пространстве V, называется гомоморфизм этой группы в группу невырожденных линейных операторов пространства V.
Задача настоящей работы состояла в самостоятельном изучении основных понятий и методов данной области и рассмотрении примеров по изучаемым темам.
В процессе написания были проработаны следующие разделы: операции симметрии молекул; классы смежности и факторизация групп; векторные, эвклидовы и унитарные пространства; представления групп и характеры представлений; операторы проектирования. Материал разбит на две главы, которые в свою очередь разбиваются на параграфы. На протяжении всего теоретического материала рассматриваются примеры, которые иллюстрируют применение изучаемых вопросов. Так большинство примеров показаны на множестве операций симметрии молекул аммиака NH3 – группе C3V.
Глава 1 Элементы теории групп симметрии молекул
1.1 Операции симметрии молекулы
1. Элементы и операции симметрии молекулы
Под геометрической конфигурацией молекулы или иона будем понимать пространственное расположение ядер атомов в молекуле или ионе относительно друг друга. Геометрическую конфигурация молекулы можно охарактеризовать, построив модель молекулы. Впервые модели молекул из шаров и стержней были построены в 1810 г. Джоном Дальтоном. Современные представления о структуре молекулы являются более точными благодаря применению точных экспериментальных методов определения этой структуры (оптические и дифракционные методы). Использовав эти методы, мы можем построить геометрическую модель молекулы в виде конечной фигуры.
Важной особенностью современных представлений о строении молекул является наличие симметрии молекул.
Определение 1. Отображением множества M на множество N называется правило f, которое каждому элементу m из множества M ставит в соответствие элемент n из множества N, называемый образом элемента m, при этом каждый элемент множества N является образом хотя бы одного элемента из множества M.
Если M=N, то говорят об отображении множества М на себя.
Определение 2. Операцией симметрии конечной фигуры называется ее изомерическое (т. е. сохраняющее расстояние между точками фигуры) отображение на себя.
Рассматривая эти примеры, приходим к заключению, что помимо геометрической модели, с молекулой аммиака необходимо связать геометрические образы – прямую C3 и плоскость 
, которые не принадлежат модели хотя бы потому, что они бесконечны
Операции симметрии пространственной фигуры, соответствующей молекуле, называются операциями симметрии молекулы.
|
|
|
|
|
|
|
|
 |
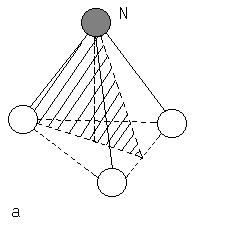
В качестве примера рассмотрим молекулу аммиака NH3. Ее геометрическая конфигурация имеет форму правильной треугольной
|
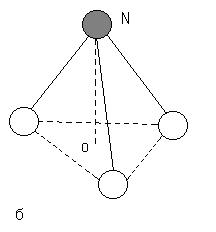
К числу операций симметрии правильной треугольной пирамиды относятся повороты, совмещающие ее с собой. Точки N и O определяют ось поворота, которую обозначим через С3. Повернем пирамиду вокруг этой оси на 120о против часовой стрелки. Указанный поворот обозначим через 
. На рис. 1, б изображена фигура (результат поворота), которая совмещается с исходной (рис. 1, а) при наложении. Рассмотрим отражение в плоскости , совмещающее фигуру с собой, и обозначим его 
. Очевидно, что , как и , является операцией симметрии молекулы аммиака, так как операции и не изменяют расстояний между точками фигуры NH3.
Рассматривая эти примеры, приходим к заключению, что помимо геометрической модели, с молекулой аммиака необходимо связать геометрические образы – прямую C3 и плоскость , которые не принадлежат модели хотя бы потому, что они бесконечны.
Определение 3. Элементом симметрии молекулы называется вспомогательный геометрический образ (точка, прямая, плоскость), характеризующий некоторое множество операций симметрии фигуры, изображающей молекулу.
Например, ось C3 характеризует множество операций симметрии, состоящее из рассмотренного нами поворота , а также поворотов 
на 240о и 
на 360о против часовой стрелки молекулы аммиака. Поворот называется тождественной операцией симметрии. При этой операции симметрии все точки геометрической модели молекулы отображаются в себя. Плоскость характеризует множество операций симметрии, состоящее из и 
.
Элементы симметрии не следует путать с операциями симметрии. Элементы симметрии будем обозначать буквами, а операции симметрии – буквами «со шляпками» над ними.
Рассмотрим множество, элементами которого являются всевозможные операции симметрии молекулы, для случая молекулы аммиака. Четыре элемента 
, , , этого множества мы уже нашли. Кроме плоскости (рис. 1, а), молекула аммиака имеет еще две плоскости симметрии 
и 
, содержащие прямые NH(2) и NH(3) соответственно. С плоскостями и связаны операции симметрии 
и . Множество операций симметрии молекулы аммиака может быть обозначено следующим образом:
.
Похожие работы
... , а затем и более фундаментального, одновременно и самого абстрактного (динамического) понимания симметрии. 2. 2.2.Симметрия кристаллов. Правильную, симметричную форму кристаллов издавна объясняли симметричным расположением атомов. Само существование атомов было еще гипотезой, но внешнее проявление стройного порядка заставляло предполагать внутреннюю причину. Быть может, правильные пирамиды, ...
... : правый рукав соответствует левому, правая штанина — левой. Пуговицы на куртке и на рубашке сидят ровно посередине, а если и отступают от нее, то на симметричные расстояния. Но на фоне этой общей симметрии в мелких деталях мы умышленно допускаем асимметрию, например расчесывая волосы на косой пробор — слева или справа. Или, скажем, помещая на костюме асимметричный кармашек на груди. Или надев ...
... требуется оценить отклонение от нулевого положения, например на руле грузовика или на штурвале корабля. Симметрия проявляется в многообразных структурах и явлениях неорганического мира и живой природы. В мир неживой природы очарование симметрии вносят кристаллы. Каждая снежинка- это маленький кристалл замерзшей воды. Форма снежинок может быть очень разнообразной, но все они обладают симметрией - ...
... ), и ее вклад в теплоемкость равен 1. Вращательная теплоемкость многоатомных газов. Свободную энергию многоатомного газа, как и двухатомного, можно представить в виде суммы трех частей — поступательной, вращательной и колебательной. Поступательная часть характеризуется теплоемкостью и химической постоянной, равными: Благодаря большой величине моментов инерции многоатомных молекул (и ...
0 комментариев