База (базис) и размерность векторного пространства

2. База (базис) и размерность векторного пространства

Пусть М – левый модуль над кольцом K. Выражение вида k₁v₁+k₂v₂+…+k_nv_n, где k_iÎK, v_iÎM, называется линейной комбинацией векторов v₁, v₂, …, v_n. Если все k_i=0, то линейная комбинация называется тривиальной. Если вектор v является линейной комбинацией векторов v₁, v₂, …, v_n, то говорят, что он выражается через систему S=<v₁, v₂, …, v_n>.

Определение 7. Конечная система векторов v₁, v₂, …, v_n векторного пространства называется линейно зависимой, если существует нетривиальная линейная комбинация этих векторов равная нулю. Система, не являющаяся линейно зависимой, называется линейно независимой.

Бесконечная система векторов векторного пространства называется линейно независимой, если любая ее конечная подсистема линейно независима.

Определение 8. Векторное пространство V называется конечномерным, имеющим разность n, если в нем найдется n линейно независимых векторов, а любые n+1 векторов линейно зависимы. Если в векторном пространстве можно указать систему из n линейно независимых векторов для любого конечного числа n, то это пространство называется бесконечномерным.

Размерность пространства обозначается в виде dim V.

Определение 9. Базисом или базой, в n-мерном векторном пространстве V называется любая ее система из n линейно независимых векторов.

Если e₁, e₂, …, e_n – база пространства V и v=x₁e₁+x₂e₂+…+x_ne_n, то числа x₁, x₂, …, x_n определяются однозначно и называются координатами вектора v в базе e₁, e₂, …, e_n. Вектор v в этом случае можно записать в виде v=( x₁, x₂, …, x_n).

2.2 Эвклидовы и унитарные пространства

1. Билинейные и квадратичные формы

Определение 1. Линейной функцией, или линейной формой, в векторном пространстве V над полем вещественных (комплексных) чисел Р называется отображение f векторного пространства V в поле Р, ставящее в соответствие каждому вектору вещественное (комплексное) число, если это отображение удовлетворяет следующим условиям:

1)   f(x+y)=f(x)+f(y);

2)   f(ax)=af(x),

где x, y - произвольные векторы из пространства V, а aÎP.

Если dimV=n, e₁, e₂, …, e_n – базис пространства V и x= x₁e₁+x₂e₂+…+x_ne_n – произвольный вектор из этого пространства, то

f(x)=f(x₁e₁+x₂e₂+…+x_ne_n)= x₁f(e₁)+x₂f(e₂)+…+x_nf(e_n) или

f(x)= a₁x₁+a₂x₂+…+a_nx_n, где a_i=f(e_i), i=1, 2, …, n.

Таким образом, при фиксированном базисе линейная функция представляется линейной формой (формой называется однородный многочлен).

Определение 2. Полулинейной формой или линейной функцией второго рода называется функция f, удовлетворяющая следующим условиям:

1) f(x+y)=f(x)+f(y)

2)

где  - число, комплексно-сопряженное с l.

Определение 3. Функция A(x, y) векторов x и y векторного пространства V над полем вещественных чисел называется билинейной функцией или билинейной формой, если при фиксированном x она является линейной функцией от y, а при фиксированном y – линейной функцией от x.

По аналогии с линейной функцией можно показать, что билинейная функция представляется билинейной формой, т. е. выражением вида

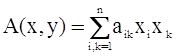, где a_ik=A(e_i, e_k).

Поэтому билинейную функцию часто тоже называют билинейной формой.

Если A(x, y)=A(y, x) при любых x и y, билинейная форма A(x, y) называется симметрической.

Определение 4. Функция A(x, x), которая получена из симметрической билинейной формы, если наложить y=x, называется квадратичной формой.

Определение 5. Функция A(x, y) называется полуторалинейной формой векторов x и y комплексного пространства или билинейной формой в комплексном векторном пространстве, если при фиксированном y форма A(x, y) есть линейная форма от x, а при фиксированном x форма A(x, y) есть полученная форма от y.

В комплексном векторном пространстве полуторалинейную функцию можно представить в виде билинейной формы 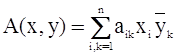, где a_ik=A(e_i, e_k).

Определение 6. Билинейная форма в комплексном пространстве называется эрмитово-симметрической или эрмитовой, если A(x, y)= для всех векторов x и y из этого пространства.

Определение 7. Эрмитовой квадратичной формой называется функция, полученная из эрмитово-симметрической формы A(x, y), если положить в ней y=x. Так как A(x, x)=, то эрмитова квадратичная форма принимает только вещественные значения.

Определение 8. Квадратичной формой на пространстве V (вещественном или комплексном) называется такое отображение  (Р – поле вещественных или комплексных чисел), для которого существует билинейная (полуторалинейная в случае Р=С) форма В(x, y) со свойством A(x)=B(x, x) для любого вектора xÎV.

Похожие работы

Проявление симметрии в различных формах материи

Скачать

90168

0

3

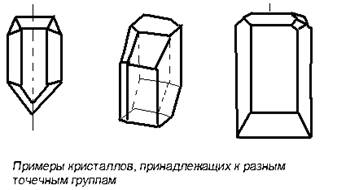
... , а затем и более фундаментального, одновременно и самого абстрактного (динамического) понимания симметрии. 2. 2.2.Симметрия кристаллов. Правильную, симметричную форму кристаллов издавна объясняли симметричным расположением атомов. Само существование атомов было еще гипотезой, но внешнее проявление стройного порядка заставляло предполагать внутреннюю причину. Быть может, правильные пирамиды, ...

Симметрия

Скачать

53953

1

0

... : правый рукав соответствует левому, правая штанина — левой. Пуговицы на куртке и на рубашке сидят ровно посередине, а если и отступают от нее, то на симметричные расстояния. Но на фоне этой общей симметрии в мелких деталях мы умышленно допускаем асимметрию, например расчесывая воло­сы на косой пробор — слева или справа. Или, скажем, помещая на костюме асимметричный кармашек на груди. Или надев ...

Симметрия в неживой природе

Скачать

53262

0

4

... требуется оценить отклонение от нулевого положения, например на руле грузовика или на штурвале корабля. Симметрия проявляется в многообразных структурах и явлениях неорганического мира и живой природы. В мир неживой природы очарование симметрии вносят кристаллы. Каждая снежинка- это маленький кристалл замерзшей воды. Форма снежинок может быть очень разнообразной, но все они обладают симметрией - ...

Влияние вращательного и поступательного движения молекул на теплоёмкость многоатомных газов

Скачать

20537

0

0

... ), и ее вклад в теплоемкость равен 1. Вращательная теплоемкость многоатомных газов. Свободную энергию многоатомного газа, как и двухатомного, можно представить в виде суммы трех частей — поступательной, вращательной и колебательной. Поступательная часть характеризуется теплоемкостью и химической постоянной, равными:   Благодаря большой величине моментов инерции многоатомных молекул (и ...