Классификация элементов симметрии молекулы
Групповые постулаты
Определение группы
Классы смежности и классы сопряженных элементов
Факторизация групп
База (базис) и размерность векторного пространства
Эвклидовы и унитарные пространства
Представления групп
Представления групп и модули
Представление алгебр и модули
Таблицы характеров неприводимых представлений
Найти всевозможные линейно независимые общие правые собственные векторы
Операторы проектирования
Разложение представления в прямую сумму неприводимых представлений с помощью оператора Вигнера
Навигация
Эвклидовы и унитарные пространства
Теория симметрии молекул
74215
знаков
5
таблиц
9
изображений
2. Эвклидовы и унитарные пространства
Определение 9. Симметрическая билинейная форма A(x, y) на вещественном пространстве (эрмитово-симметрическая форма на комплексном пространстве) называется положительно определенной, если A(x, x)>0 для любого, отличного от нуля вектора x из рассматриваемого пространства.
Определение 9¢. Квадратичная форма (эрмитова квадратичная форма) называется положительно определенной, если для любого вектора x¹0 она принимает положительное значение.
Определение 10. n-мерным эвклидовым (унитарным) пространством называется n-мерное вещественное (комплексное) векторное пространство с положительно определенным симметрическим (эрмитовым) скалярным произведением.
Все вводимые далее понятия пригодны как для эвклидовых, так и для унитарных пространств.
Определение 11. База e1, e2, …, en эвклидова (унитарного) пространства называется ортогональной, если (ei, ej)=0, i¹j, i, j=1, 2, …, n, и ортонормированной, если она ортогональна и длина всех векторов равны единице.
3. Изометрия эвклидовых и унитарных пространств
Определение 12. Взаимно однозначное отображение f модуля М на модуль М¢ над одним и тем же кольцом K называется изоморфизмом, если выполняются следующие условия:
1. f(x, y)=f(x)+f(y)=x¢+y¢; x¢=f(x); y¢=f(y);
"x, yÎM;
2. f(ax)=af(x)=ax¢; "xÎK; "xÎM; x¢=f(x)ÎM¢.
Определение 13. Два векторных пространства W и W¢ над полем Р называются изоморфными, если они изморфны как модули над кольцом, которым является поле Р.
Пусть теперь даны два векторных пространства W и W¢ со скалярными произведениями A(x, y) и A¢(x¢, y¢) над полем Р.
Определение 14. Изометрией векторных пространств W и W¢ называется любой их изморфизм, который сохраняет значения всех скалярных произведений, т. е.
A(x, y)= A¢(f(x), f(y))= A¢(x¢, y¢); "x, yÎW;
f(x)=x¢; f(y)=y¢.
В эвклидовом пространстве из определения длины вектора и угла между двумя векторами следует, что при изометрии сохраняются длины векторов и углы между ними, т. е. сохраняются метрические соотношения, чем и объясняется название «изометрия». В унитарном пространстве при изометрии сохраняются длины векторов, ортогональные векторы переходят в ортогональные векторы.
2.3 Матрицы
1. Линейные отображения, операторы и матрицы
Определение 1. Отображение f: V®W векторного пространства V в векторное пространство W над полем Р называется линейное отображение, если для всех v, v1, v2ÎV, aÎP выполняются условия:
1) f(v1+v2)=f(v1)+f(v2);
2) f(av)=af(v).
Если V=W, то линейное отображение называется линейным оператором или линейным преобразованием пространства V.
Пусть e1, e2, …, en – базис пространства V, а e1¢, e2¢, …, en¢ - базис пространства W. Образы базисных векторов пространства V в базисе пространства W можно записать в виде
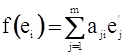(i=1, 2, …, m) (1)
Коэффициенты в выражении (1) запишем в виде матрицы, которая называется матрицей линейного отображения f.
.
В случае линейных операторов, т. е. линейных отображений векторного пространства в себя, операторы удобно обозначать 
, а матрицу оператора в фиксированном базисе – в виде А.
2. Унитарные, ортогональные, эрмитовы операторы и матрицы
Определение 2. Линейные операторы эвклидова (унитарного) пространства, которые сохраняют скалярное произведение векторов этого пространства, называется ортогональными (унитарными) операторами.
Пусть e1, e2, …, en – ортонормированная база унитарного (эвклидова) пространства. Если - унитарный (ортогональный) оператор, то согласно его определению
(ei, ej)= (ei, ei)=1, i=1, 2, …, n;
(ei, ej)= (ei, ej)=0, i¹y. (2)
Это означает, что система векторов e1, e2, …, en сама составляет ортонормированную базу в соответствующем пространстве.
Пусть А – матрица унитарного (ортогонального) оператора. Тогда можно записать 
. Из выражения (2) следует, что в матрице А скалярные произведения векторов-столбцов на себя равны единице, а скалярное произведение различных векторов-стобцов равно нулю. Такая матрица называется унитарной (ортогональной). Унитарность (ортогональность) матрицы А означает, что сумма произведений элементов, стоящих в любом столбце этой матрицы, на сопряженные (на те же самые) к ним элементы равны единице, а сумма произведений элементов любого столбца на сопряженные к ним (на соответственные к ним) элементы другого столбца равна нулю.
Определение 3. Матрица А* называется эрмитово сопряженной (или просто сопряженной) по отношению к матрице А, если А*=
, т. е. для того, чтобы из матрицы А получить эрмитово сопряженную матрицу, ее надо транспонировать и заменить элементы транспонированной матрицы комплексно-сопряженными элементами.
Определение 4. Матрица А называется самосопряженной или эрмитовой матрицей, если A=A*; в том же случае, если элементы матрицы вещественны, A*=At=A и матрица А называется симметрической матрицей.
Определение 5. Матрица А называется унитарной (ортогональной) матрицей, если A*=A-1 (если At=A-1). Операторы, соответствующие эрмитовым матрицам, будем называть эрмитовыми.
Похожие работы
... , а затем и более фундаментального, одновременно и самого абстрактного (динамического) понимания симметрии. 2. 2.2.Симметрия кристаллов. Правильную, симметричную форму кристаллов издавна объясняли симметричным расположением атомов. Само существование атомов было еще гипотезой, но внешнее проявление стройного порядка заставляло предполагать внутреннюю причину. Быть может, правильные пирамиды, ...
... : правый рукав соответствует левому, правая штанина — левой. Пуговицы на куртке и на рубашке сидят ровно посередине, а если и отступают от нее, то на симметричные расстояния. Но на фоне этой общей симметрии в мелких деталях мы умышленно допускаем асимметрию, например расчесывая волосы на косой пробор — слева или справа. Или, скажем, помещая на костюме асимметричный кармашек на груди. Или надев ...
... требуется оценить отклонение от нулевого положения, например на руле грузовика или на штурвале корабля. Симметрия проявляется в многообразных структурах и явлениях неорганического мира и живой природы. В мир неживой природы очарование симметрии вносят кристаллы. Каждая снежинка- это маленький кристалл замерзшей воды. Форма снежинок может быть очень разнообразной, но все они обладают симметрией - ...
... ), и ее вклад в теплоемкость равен 1. Вращательная теплоемкость многоатомных газов. Свободную энергию многоатомного газа, как и двухатомного, можно представить в виде суммы трех частей — поступательной, вращательной и колебательной. Поступательная часть характеризуется теплоемкостью и химической постоянной, равными: Благодаря большой величине моментов инерции многоатомных молекул (и ...
0 комментариев