Разложение представления в прямую сумму неприводимых представлений с помощью оператора Вигнера

4. Разложение представления в прямую сумму неприводимых представлений с помощью оператора Вигнера

Обозначим через М модуль, связанный с представлением Т. Пусть неприводимым представлениям Т₁, Т₂, …, Т_t из канонического разложения представления согласно методу, описанному ранее (см. § 4), соответствуют неприводимые подмодули М₁, М₂, …, М_t. Разложение модуля М вида

 (34)

называется каноническим разложением модуля М. Обозначим n_iM_i=L_i, так, что

. (35)

Неприводимые подмодули модулей L_i обозначим

; i=1, 2, …, t. (36)

Эти модули нам необходимо найти.

Предположим, что задача решена. Следовательно, в каждом из модмодулей M_i^(s) (s=1, 2, …, n_i) найдена ортонормированная база , в которой оператор  представлен матрицей Т_i(g) неприводимого представления Т, полученного в результате действия (по правилу из § 3) оператора  на базу по формуле

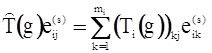, j=1, 2, …, m_i. (37)

В этом выражении можно считать, что m_i – размерность неприводимого представления T_i(i=1, 2, …, t), причем  - элементы базы с номером g из неприводимого подмодуля M_i. Разместим теперь элементы базы L_i при фиксированном i следующим образом:

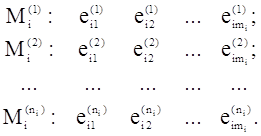 (38)

Справа в выражении (38) расположены базы модулей M_i⁽¹⁾, M_i⁽²⁾, …, . Если же i изменять от 1 до t, то получим искомую базу всего модуля М, состоящего из m₁n₁+ m₂n₂+…+ m_tn_t элементов.

Рассмотрим теперь оператор

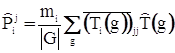, (39)

действующий в модуле М (j фиксировано). Согласно теореме 2,  - оператор проектирования. Поэтому этот оператор оставляет без изменения все базисные элементы  (s=1, 2, …, n_i), расположенные в j-м столбце выражения (38), и обращает в нуль все остальные векторы базы. Обозначим через M_ij векторное пространство, натянутое на ортогональную систему векторов , стоящие в j-м столбце выражения (38). Тогда можно сказать, что  является оператором проектирования на пространство M_ij. Оператор  известен, так как известны диагональные элементы матриц неприводимых представлений групп, а также оператор T(g).

Теперь можно решить нашу задачу.

Выберем n_i произвольных базисных векторов в M:  и подействуем на них оператором проектирования . Полученные векторы лежат в пространстве M_ij и являются линейно независимыми. Они не обязательно ортогональны и нормированы. Ортонормируем полученную систему векторов согласно правилу из § 2. Полученную систему векторов обозначим e_ij^(s) в соответствии с обозначениями, принятыми в предположении, что задача решена. Как уже обозначалось, здесь j фиксировано, а s=1, 2, …, n_i. Обозначим e_if^(s) (f=1, 2, …, j-1, j+1, …, m_i), остальные элементы базы модуля M_i размерности n_im_i. Обозначим через  следующий оператор:

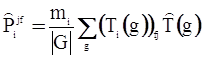. (40)

Из соотношений ортогональности для матриц неприводимых представлений следует, что этот оператор дает возможность получить e_ig^s по формуле

, i=1, 2, …, t. (41)

Все сказанное можно выразить в виде следующего алгоритма.

Для того, чтобы найти базу модуля М из элементов, преобразующихся по неприводимым представлениям Т_i, содержащихся в представлении Т, связанном с модулем М, необходимо:

1.По формуле (32) найти размерности подпространств М_ij, соответствующих j-компоненте неприводимого представления T_i.

2.Найти с помощью оператора проектирования (39) все подпространства M_ij.

3.В каждом подпространстве M_ij выбрать произвольную ортонормированную базу.

4.Используя формулу (41), найти все элементы базы, преобразующихся по остальным компонентам неприводимого представления Т_i.

Заключение

Группы – один из основных типов алгебраических систем, а теория групп – один из основных разделов современной алгебры. Понадобилась работа нескольких поколений математиков прежде чем идея групп выкристаллизовалась с ее сегодняшней ясностью. От Лагранжа через работы Руффини и Абеля к Эваристу Галуа, в работах которого уже достаточно сознательно используется идея группы (им же впервые введен и сам термин), - вот путь, по которому развивалась эта идея в рамках теории алгебраических уравнений. В настоящее время теория групп является одной из самых развитых областей алгебры, имеющей многочисленные применения в как в самой математике, так и за ее пределами – в топологии, теории функций, кристаллографии, квантовой механике и других областях математики и естествознания. Конечной целью собственно теории групп является описание всех групповых композиций.

Понятие группы позволяет в точных терминах охарактеризовать симметричность той или иной геометрической фигуры. Именно с таких позиций Е.С. Федоров решил задачу классификации правильных пространственных систем точек, являющуюся одной из основных задач кристаллографии.

Независимо и по другим причинам идея группы возникла в геометрии, когда в середине XIX в. на смену единой античной геометрии пришли многочисленные «геометрии» и остро встал вопрос об установлении связей и родства между ними. Выход был указан «Эрлангенской программой» Клейна, положившей в основу классификации геометрий понятие группы преобразований.

Лежащее в фундаменте современной математики понятие группы является весьма разносторонним орудием самой математики. Вместе с тем группы – это мощный инструмент познания одной из наиболее глубоких закономерностей реального мира – симметрии.

Список использованной литературы

1.   Морозов В.П., Дышлис А.А. Лекции по теории симметрии молекулы: Учеб. пособие. – Днепропетровск: Изд-во ДГУ, 1991. – 180 с.

2.   Александров П.С. Введение в теорию групп. – М.: Наука. Главная редакция физико-математической лит-ры, 1980 – 144 с.

3.   Каргаполов М.И., Мерзляков Ю.И. Основы теории групп – 4-е изд., перераб. – М.: Наука. Физматлит, 1996 – 288 с.

4.   Минкин В.И., Симкин Б.Я., Миняев Р.М. Теория строения молекул./ Серия «Учебники и учебные пособия». Ростов-на-Дону: «Феникс», 1997 – 560 с.

5.   Дей К., Селби Д. Теоретическая неорганическая химия. Пер. с англ.; под ред. д-ра хим. наук К.В. Астахова. Изд. 3-е, испр. и доп. М., «Химия», 1976 – 568 с.

6.   Виленкин Н.Я. Специальные функции и теория представлений групп. – М.: Наука, 1965 – 588 с.

7.   Глинка Н.Л. Общая химия: Учеб. пособие для ВУЗов, - 23-е изд., испр./ Под ред. В.А. Рабиновича. – Л.: Химия, 1983 – 704 с.

8.   Курош А.Г. Курс высшей алгебры – М.: Наука, 1971 – 432 с.

Похожие работы

Проявление симметрии в различных формах материи

Скачать

90168

0

3

... , а затем и более фундаментального, одновременно и самого абстрактного (динамического) понимания симметрии. 2. 2.2.Симметрия кристаллов. Правильную, симметричную форму кристаллов издавна объясняли симметричным расположением атомов. Само существование атомов было еще гипотезой, но внешнее проявление стройного порядка заставляло предполагать внутреннюю причину. Быть может, правильные пирамиды, ...

Симметрия

Скачать

53953

1

0

... : правый рукав соответствует левому, правая штанина — левой. Пуговицы на куртке и на рубашке сидят ровно посередине, а если и отступают от нее, то на симметричные расстояния. Но на фоне этой общей симметрии в мелких деталях мы умышленно допускаем асимметрию, например расчесывая воло­сы на косой пробор — слева или справа. Или, скажем, помещая на костюме асимметричный кармашек на груди. Или надев ...

Симметрия в неживой природе

Скачать

53262

0

4

... требуется оценить отклонение от нулевого положения, например на руле грузовика или на штурвале корабля. Симметрия проявляется в многообразных структурах и явлениях неорганического мира и живой природы. В мир неживой природы очарование симметрии вносят кристаллы. Каждая снежинка- это маленький кристалл замерзшей воды. Форма снежинок может быть очень разнообразной, но все они обладают симметрией - ...

Влияние вращательного и поступательного движения молекул на теплоёмкость многоатомных газов

Скачать

20537

0

0

... ), и ее вклад в теплоемкость равен 1. Вращательная теплоемкость многоатомных газов. Свободную энергию многоатомного газа, как и двухатомного, можно представить в виде суммы трех частей — поступательной, вращательной и колебательной. Поступательная часть характеризуется теплоемкостью и химической постоянной, равными:   Благодаря большой величине моментов инерции многоатомных молекул (и ...