Представления групп

2.4 Представления групп

1. Определение представлений

Определение 1. Представлением группы, действующим в n-мерном векторном пространстве V, называется гомоморфизм этой группы в группу невырожденных линейных операторов пространства V.

Невырожденным называется такой оператор , который имеет обратный оператор , дающий по определению в произведении с  единичный оператор : ==.

Определение 2. Матричным представлением группы G называется гомоморфизм этой группы в группу невырожденных комплексных или действительных матриц размера n´n.

Определение 3. Подстановочным представлением группы G называется гомоморфизм этой группы в группу подстановок порядка n. Если гомоморфизм группы G в группу операторов, матриц или подстановок является изморфизмом, то он называется точным представлением.

Представление группы будем обозначать буквой Т. Пусть g₁ и g₂ – любые элементы группы G, а Т(g₁) и Т(g₂) – соответствующие этим элементам матрицы представления. Тогда согласно определению гомоморфизма группы

Т(g₁, g₂)= Т(g₁) Т(g₂). (4)

Определение 4. Два матричных представления Т₁ и Т₂ группы G в некоторую группу матриц называется эквивалентным, если существует невырожденная матрица F такая, что для всех матриц Т₁(g), Т₂(g) представления будет иметь место равенство

Т₂(g)=Ф^-1 Т₁(g)Ф, "gÎG (5)

Эквивалентные представления не различаются.

2. Приводимые и неприводимые представления

Воспользуемся языком линейных операторов. Пусть дано некоторое представление Т группы G, действующее в векторном пространстве V. Каждому вектору vÎV оператор (g)º сопоставляет вектор (v)=v₁ этого же пространства. Пусть W – подпространство пространства V.

Определение 5. Подпространство W пространства V называется инвариантным подпространством действия , если, каковы бы ни были элементы gÎG и векторы wÎW, T(w)=w₁, где w₁ÎW.

Определение 6. Представление T группы G, действующее в векторном пространстве V над полем Р, называется приводимым представлением, если в этом пространстве существуют неприводимые инвариантные относительно этого действия подпространства. Представление Т называется неприводимым, если единственные его инвариантные подпространства – О и само пространство V.

Интерпретируем это определение на языке матриц. Пусть представление Т группы G приводимо. Значит, в пространстве V представления может быть найдено нетривиальное инвариантное подпространство W. Пусть e₁, e₂, …, e_k – базис пространства W. Дополним его до базиса е₁, е₂, …, е_k, e_k+1, …, e_n всего пространства V. Так как W инвариантно, то (е_i), где i=1, 2, …, k лежат в W. Поэтому

(е_i)=a_1ie₁+a_2ie₂+…+a_kie_k, i=1, 2, …, k.

Но так как эти векторы лежат и в пространстве V, то можно также написать

(е_i)=a_1ie₁+a_2ie₂+…+a_kie_k+0e_k+1+…+0e_n, i=1, 2, …, k.

Что же касается отдельных базисных векторов e_k+1, e_k+2, …, e_n, то, поскольку они не принадлежат W, их образы выражаются через базис наиболее общим способом и получаем следующую картину:

(е₁)=a₁₁e₁+a₂₁e₂+…+a_k1e_k+0e_k+1+…+0e_n

(е₂)=a₁₂e₁+a₂₂e₂+…+a_k2e_k+0e_k+1+…+0e_n

(е_k)=a_1ke₁+a_2ke₂+…+a_kke_k+0e_k+1+…+0e_n

(е_k+1)=a_1,k+1e₁+a_2,k+1e₂+…+a_k,k+1e_k+ a_k+1,k+1e_k+1+…+a_n,k+1e_n

(е_n)=a_1ne₁+a_2ne₂+…+a_kne_k+ a_k+1,ne_k+1+…+a_nne_n.

Отсюда видно, что матрицы всех элементов группы G в предствлении Т будут одновременно иметь следующий вид:

 (6)

Поэтому на языке матриц матричное представление называется приводимым, если все матрицы его могут быть записаны при определенном выборе базиса в виде (6). Если же ни при каком выборе базиса матрицы представления нельзя записать в указанном виде, представления называются неприводимыми.

Похожие работы

Проявление симметрии в различных формах материи

Скачать

90168

0

3

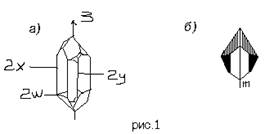
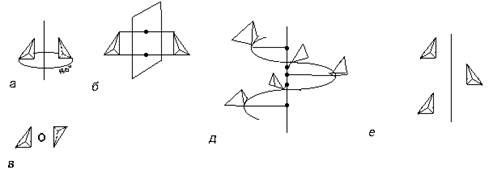
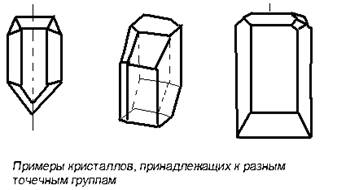
... , а затем и более фундаментального, одновременно и самого абстрактного (динамического) понимания симметрии. 2. 2.2.Симметрия кристаллов. Правильную, симметричную форму кристаллов издавна объясняли симметричным расположением атомов. Само существование атомов было еще гипотезой, но внешнее проявление стройного порядка заставляло предполагать внутреннюю причину. Быть может, правильные пирамиды, ...

Симметрия

Скачать

53953

1

0

... : правый рукав соответствует левому, правая штанина — левой. Пуговицы на куртке и на рубашке сидят ровно посередине, а если и отступают от нее, то на симметричные расстояния. Но на фоне этой общей симметрии в мелких деталях мы умышленно допускаем асимметрию, например расчесывая воло­сы на косой пробор — слева или справа. Или, скажем, помещая на костюме асимметричный кармашек на груди. Или надев ...

Симметрия в неживой природе

Скачать

53262

0

4

... требуется оценить отклонение от нулевого положения, например на руле грузовика или на штурвале корабля. Симметрия проявляется в многообразных структурах и явлениях неорганического мира и живой природы. В мир неживой природы очарование симметрии вносят кристаллы. Каждая снежинка- это маленький кристалл замерзшей воды. Форма снежинок может быть очень разнообразной, но все они обладают симметрией - ...

Влияние вращательного и поступательного движения молекул на теплоёмкость многоатомных газов

Скачать

20537

0

0

... ), и ее вклад в теплоемкость равен 1. Вращательная теплоемкость многоатомных газов. Свободную энергию многоатомного газа, как и двухатомного, можно представить в виде суммы трех частей — поступательной, вращательной и колебательной. Поступательная часть характеризуется теплоемкостью и химической постоянной, равными:   Благодаря большой величине моментов инерции многоатомных молекул (и ...