Классификация элементов симметрии молекулы
Групповые постулаты
Определение группы
Классы смежности и классы сопряженных элементов
Факторизация групп
База (базис) и размерность векторного пространства
Эвклидовы и унитарные пространства
Представления групп
Представления групп и модули
Представление алгебр и модули
Таблицы характеров неприводимых представлений
Найти всевозможные линейно независимые общие правые собственные векторы
Операторы проектирования
Разложение представления в прямую сумму неприводимых представлений с помощью оператора Вигнера
Навигация
Операторы проектирования
Теория симметрии молекул
74215
знаков
5
таблиц
9
изображений
2.6 Операторы проектирования
1. Операторы проектирования и идемпотенты кольца
Пусть векторное пространство V равно прямой сумме подпространств W и L: 
. По определению прямой суммы это означает, что каждый вектор vÎV однозначно представим в виде v=w+l, wÎW. lÎL.
Определение 1. Если , так что v=w+l, то отображение 
, сопоставляющая каждому вектору vÎV его компоненту (проекцию) wÎW, называется проектором пространства V на пространство W. 
называют также оператором проектирования, или проекционным оператором.
Очевидно, если wÎW, то (w)=w. Отсюда следует, что обладает следующим замечательным свойством 2=Р.
Определение 2. Элемент е кольца K называется идемпотентом (т. е. подобным единице), если е2=е.
В кольце целых чисел есть всего два идемпотента: 1 и 0. Иное дело в кольце матриц. Например, матрицы 
, 
, 
,
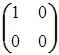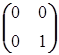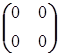- идемпотенты. Матрицы операторов проектирования также идемпотенты. Соответствующие им операторы называются идемпотентными операторами.
Рассмотрим теперь прямую сумму n подпространств пространства V:
.
Тогда аналогично случаю прямой суммы двух подпространств можем получить n операторов проектирования 
, 
, …, 
. Они обладают свойством 
==0 при i¹j.
Определение 3. Идемпотенты ei и ej (i¹j) называются ортогональными, если ei ej= ej ei=0. Следовательно, и - ортогональные идемпотенты.
Из того, что IV=V, и из правила сложения линейных операторов следует, что
.
Это разложение называется разложением единицы в сумму идемпотентов.
Определение 4. Идемпотент е называется минимальным, если его нельзя представить в виде суммы идемпотентов, отличных от е и 0.
2. Каноническое разложение представления
Определение 5. Каноническим разложением представления Т(g) называется его разложение вида Т(g)=n1T1(g)+ n2T2(g)+…+ ntTt(g), в котором эквивалентные неприводимые представления Тi(g) объединены вместе, причем ni – кратность вхождения неприводимого представления Ti(g) в разложение T(g).
Теорема 1. Каноническое разложение представления определяется с помощью проекционного оператора вида
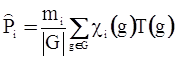, i=1, 2, …, t, (31)
где |G| - порядок группы G; mi – степени представлений Ti(g), где i=1, 2, …, t; ci(g), i=1, 2, …, t – характеры неприводимых представлений Ti(g). При этом mi определяется по формуле
. (32)
3. Проекционные операторы, связанные с матрицами неприводимых представлений групп
С помощью формул (31) можно получить только каноническое разложение представления. В общем случае, надо воспользоваться матрицами неприводимых представлений, которые позволяют построить соответствующие операторы проектирования.
Теорема 2. Пусть 
- матричные элементы неприводимого представления Tr(g) группы G. Оператор вида
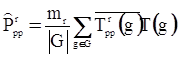(33)
является оператором проектирования и называется оператором Вигнера. В выражении (33) mr – размерность представления Tr(g).
Похожие работы
... , а затем и более фундаментального, одновременно и самого абстрактного (динамического) понимания симметрии. 2. 2.2.Симметрия кристаллов. Правильную, симметричную форму кристаллов издавна объясняли симметричным расположением атомов. Само существование атомов было еще гипотезой, но внешнее проявление стройного порядка заставляло предполагать внутреннюю причину. Быть может, правильные пирамиды, ...
... : правый рукав соответствует левому, правая штанина — левой. Пуговицы на куртке и на рубашке сидят ровно посередине, а если и отступают от нее, то на симметричные расстояния. Но на фоне этой общей симметрии в мелких деталях мы умышленно допускаем асимметрию, например расчесывая волосы на косой пробор — слева или справа. Или, скажем, помещая на костюме асимметричный кармашек на груди. Или надев ...
... требуется оценить отклонение от нулевого положения, например на руле грузовика или на штурвале корабля. Симметрия проявляется в многообразных структурах и явлениях неорганического мира и живой природы. В мир неживой природы очарование симметрии вносят кристаллы. Каждая снежинка- это маленький кристалл замерзшей воды. Форма снежинок может быть очень разнообразной, но все они обладают симметрией - ...
... ), и ее вклад в теплоемкость равен 1. Вращательная теплоемкость многоатомных газов. Свободную энергию многоатомного газа, как и двухатомного, можно представить в виде суммы трех частей — поступательной, вращательной и колебательной. Поступательная часть характеризуется теплоемкостью и химической постоянной, равными: Благодаря большой величине моментов инерции многоатомных молекул (и ...
0 комментариев