Расчёт надёжности системы с постоянным общим резервированием

1.20 Расчёт надёжности системы с постоянным общим резервированием

Резервирование называется общим, если резервируется вся система, состоящая из последовательного соединения n элементов.

Основная цепь содержит n элементов.

Число резервных цепей равно m, кратность резервирования равна m. Общее число резервных элементов равно mn.

Определим количественные характеристики надёжности в случае постоянного включения резервных цепей.

Введём обозначения

 i = 1, 2, ……..,n - вероятность безотказной работы элемента Эio ;

 j = 1, 2, ……..,m; i = 1, 2, …….,n - вероятность безотказной работы элемента Эij.

Запишем вероятность безотказной работы j - ой цепи

 j = 0, 1, ……,m (1.7)

Вероятность отказа j - ой цепи

 (1.8)

Определим вероятность безотказной работы системы

 (1.9)

Подставим (1.7) в (1.9). Получим

Определим вероятность безотказной работы системы

Частный случай: основная и резервные цепи имеют одинаковую надёжность, т.е.

Тогда

;

;

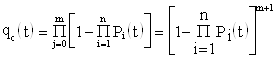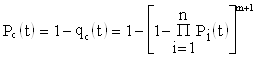Рассмотрим экспоненциальный закон надёжности, т.е.

Тогда ;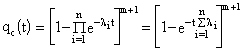

 или  

 - интенсивность отказов цепи, состоящей из n элементов.

Вероятность безотказной работы системы.

Определим интенсивность отказов системы

;

 ;

Определим среднее время безотказной работы резервированной системы

где  - среднее время безотказной работы нерезервированной системы.

Т.о. с увеличением кратности резервирования m среднее время безотказной работы растёт, но очень медленно. Наибольший прирост наблюдается при переходе от нерезервированной системы к резервированной с кратностью m = 1.

1.21 Расчёт надёжности системы с постоянным поэлементным резервированием

При поэлементном резервировании резервируются отдельно элементы системы.

Определим количественные характеристики надёжности системы.

Введём обозначения:

 i = 1, 2, ……..,n - вероятность безотказной работы элемента Эio на интервале времени (0, t);

 j = 1, 2, ……..,m; i = 1, 2, …….,n - вероятность безотказной работы элемента Эij на интервале времени (0, t).

Запишем вероятность отказа i - й группы.

Имеем

 i = 1, 2, …….,n.

Запишем вероятность безотказной работы i - ой группы. Имеем

Запишем вероятность безотказной работы системы с поэлементным резервированием

или

Для равнонадёжных элементов системы имеем:

1.22 Режим облегченного (тёплого) резерва

Рассмотрим случай, когда время безотказной работы всех элементов изделия подчиняется экспоненциальному закону распределения. В этом случае процессы, характеризующие работу изделия являются марковскими. Для определения характеристик надёжности можно использовать математический аппарат теории марковских случайных процессов.

В режиме облегченного резерва резервные элементы находятся в режиме недогрузки до момента их включения в работу. Пусть l1 - интенсивность отказа резервного элемента в режиме недогрузки до момента их включения в работу. l0 - интенсивность отказа резервного элемента в состоянии работы.

Введём в рассмотрение состояния ,

S0 - основной элемент исправен и работает, m резервных элементов исправны и находятся в режиме недогрузки.

S1 - основной элемент отказал, работает 1 - ый резервный элемент, (m - 1) резервные элементы исправны и находятся в режиме недогрузки.

S2 - отказал 1 - ый резервный элемент, работает 2 - ой резервный элемент, (m - 2) резервных элементов исправны и находятся в режиме недогрузки.

Si - отказал i - й резервный элемент, работает i - й резервный элемент, (m - i ) резервных элементов исправны и находятся в режиме недогрузки.

Sm - отказал (m - 1) - ый элемент, работает m - ый резервный элемент.

Sm+1 - отказал m -ый резервный элемент.

Запишем систему дифференциальных уравнений Колмогорова. Для этого введём обозначения:

P0(t) - вероятность нахождения резервированной системы в момент времени t в состоянии S0.

Pi(t) - вероятность нахождения резервированной системы в момент времени t в состоянии Si , i = 0, 1, ….., m, m + 1.

;

 ………………………………………………….

………………………………………………….

.

Начальные условия:

.

Применим к системе дифференциальных уравнений Колмогорова преобразование Лапласа. Получим систему линейных алгебраических уравнений вида: Pi(t) - оригинал

Pi(S) - изображение по Лапласу

 i = 0, 1, ……, m +1

…………………………………………….

…………………………………………….

Решая систему уравнений получим

Найдём оригинал . Имеем

где

Здесь - вероятность отказа резервированной системы с облегченным резервированием.

Определим вероятность безотказной работы системы с облегченным резервированием. Имеем:

Определим среднее время безотказной работы системы с облегченным резервированием. Имеем:

Формула бинома Ньютона

где

При a = 1 имеем:

Выполнив преобразование, получим:

 где .

Определим частоту отказов  резервированной системы. Имеем

;

или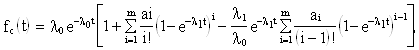

Определим интенсивность отказов  резервированной системы. Имеем

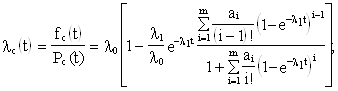
Похожие работы

Разработка программно–алгоритмических средств для определения надёжности программного обеспечения на основании моделирования работы системы типа "клиент–сервер"

Скачать

104437

5

35

... первоначальное количество ошибок можно оценить как: Поставленная задача позволяет определить такие важные характеристики функционирования программного комплекса, как: расчет текущего времени наработки до отказа; расчет среднего времени наработки до отказа за все время моделирования работы системы; расчет вероятности отказа ПО в единицу расчёт коэффициента готовности Таким образом, наша ...

Классификация автоматизированных систем управления

Скачать

22140

0

0

... , что каждый из них можно представить как шкалу в многомерном фазовом пространстве, тогда конкретным АСУ в этом пространстве будут соответствовать точки или определенные области.   2.2. Классификация систем и автоматизация управления сложными системами Прежде всего система – это целостная совокупность некоторых элементов, не сводящаяся к простой сумме своих частей, т.е. представляющая собой ...

Автоматизация и диспетчеризация систем электроснабжения

Скачать

129027

5

16

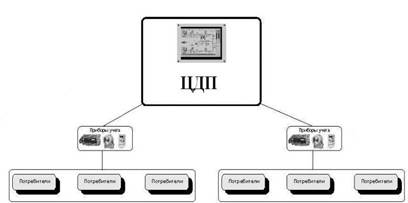
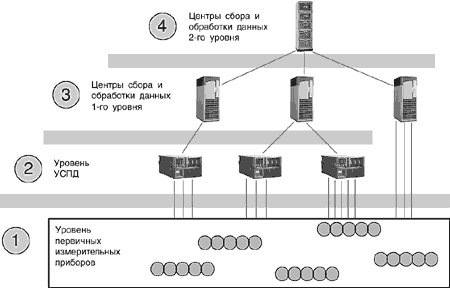
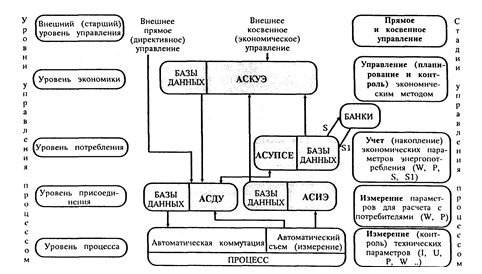
... разных этапах производства (потребления) электроэнергии. Основная цель создания таких систем – дальнейшеё повышение эффективности технических и программных средств автоматизации и диспетчеризации СЭС для улучшения технико-экономических показателей и повышения качества и надёжности электроснабжения ПП. Реформирование электроэнергетики России требует создания полномасштабных иерархических систем ...

Автоматизированная система контроля знаний специалистов по дефектоскопии

Скачать

131566

7

26

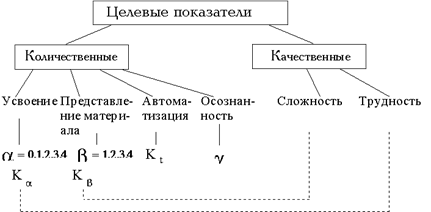
... , повысить вероятность выявления дефектов и, с другой стороны, снизить различные технико-экономические затраты на проведение контроля. 2. Проектирование системы контроля знаний 2.1 Общая структура системы По своей логической структуре система состоит из трёх частей: -            подсистемы конфигурирования теста; -            подсистемы тестирования; -            подсистема сервиса. ...