Навигация
Критерий Пирсона
1.14 Критерий Пирсона
Разбиваем полученные в опытах значения Т на k интервалов:
k - число интервалов. Выдвигаем гипотезу H о том, что выбранная теоретическая плотность вероятности случайной величины Т есть функция f(t).
В качестве величины ![]() выбираем величину
выбираем величину ![]() , определяемую по формуле
, определяемую по формуле
![]() ;
;
где n - число опытов (число отказов);
![]() - частота попадания случайной величины Т в интервал
- частота попадания случайной величины Т в интервал ![]() ;
;
![]() - количество значений случайной величины Т, попавших в интервал
- количество значений случайной величины Т, попавших в интервал ![]() ;
;
![]() - вероятность попадания случайной величины Т в интервал
- вероятность попадания случайной величины Т в интервал ![]() ;
;
![]() ;
; ![]() ; i = 1, 2, …., K;
; i = 1, 2, …., K; 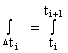 ;
;
![]() - это случайная величина.
- это случайная величина.
Можно доказать, что если верна гипотеза Н, то при ![]() распределение величины
распределение величины ![]() независимо от вида функции f(t) стремится к распределению
независимо от вида функции f(t) стремится к распределению ![]() с числом степеней свободы
с числом степеней свободы
![]() ; где K - число интервалов, r - число параметров функции f(t), оцениваемых по результатам опытов, по результатам статистической выборки объёма n.
; где K - число интервалов, r - число параметров функции f(t), оцениваемых по результатам опытов, по результатам статистической выборки объёма n.
Т.о. при ![]()
![]()
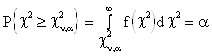 ;
;
Пусть ![]() - такое число, что можно считать практически невозможным осуществление события с такой вероятностью
- такое число, что можно считать практически невозможным осуществление события с такой вероятностью ![]() .
.
Если ![]() то
то ![]() .
.
маловероятное событие для гипотезы Н.
Т.о, в этом случае гипотеза Н отклоняется, т.е выбранная теоретическая плотность вероятности не согласуется с результатами опытов.
![]()
![]()
![]()
![]()
Область ![]() Область
Область ![]()
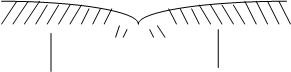
![]() - область принятия гипотезы Н (выбранная теоретическая плотность вероятности согласуется с результатами опытов).
- область принятия гипотезы Н (выбранная теоретическая плотность вероятности согласуется с результатами опытов).
![]() - область отклонения гипотезы Н.
- область отклонения гипотезы Н.
![]() , n - порядка сотен.
, n - порядка сотен.
1.15 Критерий Колмогорова
Критерий Пирсона можно применять как для непрерывных, так и для дискретных случайных величин. Критерий Колмогорова применяется только для непрерывных случайных величин.
При использовании критерия Колмогорова сравниваются статистическая функция распределения ![]() случайной величины Т и выбранная теоретическая функция распределения q(t). Предполагается, что значения параметров функции q(t) известны.
случайной величины Т и выбранная теоретическая функция распределения q(t). Предполагается, что значения параметров функции q(t) известны.
Если параметры теоретической функции распределения q(t) неизвестны, то вместо параметров могут использоваться оценки этих параметров, полученные по результатам опытов, т.е. по статистической выборке. В этом случае принимают ![]() .
.
Определяем
![]() .
.
Определяем величину ![]()
![]() ;
;
![]() - случайная величина.
- случайная величина.
Выдвигаем гипотезу Н о том, что выбранная нами теоретическая функция распределения ![]() не противоречит статистической функции распределения
не противоречит статистической функции распределения ![]() .
.
Колмогоров доказал следующую теорему.
Если верна гипотеза Н, то при ![]() независимо от вида функции q(t) случайная величина
независимо от вида функции q(t) случайная величина ![]() имеет функцию распределения вида
имеет функцию распределения вида
![]() ;
;
тогда
![]() .
.
Методика проверки гипотезы Н по критерию Колмогорова:
1) определяем статистическую функцию распределения ![]() ;
;
2) определяем ![]() ;
;
3) для заданного ![]() определяем
определяем ![]() по таблице распределения Колмогорова.
по таблице распределения Колмогорова.
Если ![]()
![]()
![]() , то проверяемая гипотеза Н отклоняется, т.е. выбранная теоретическая функция распределения q(t) не согласуется (противоречит) статистической функции распределения
, то проверяемая гипотеза Н отклоняется, т.е. выбранная теоретическая функция распределения q(t) не согласуется (противоречит) статистической функции распределения ![]() .
.
Если ![]() <
< ![]() , то проверяемая гипотеза Н принимается, т.е. теоретическая функция распределения q(t) не противоречит функции распрделения
, то проверяемая гипотеза Н принимается, т.е. теоретическая функция распределения q(t) не противоречит функции распрделения ![]() .
.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Область ![]() Область
Область ![]()
![]() - область принятия гипотезы Н,
- область принятия гипотезы Н,
![]() - область отклонения гипотезы Н.
- область отклонения гипотезы Н.
Похожие работы
... первоначальное количество ошибок можно оценить как: Поставленная задача позволяет определить такие важные характеристики функционирования программного комплекса, как: расчет текущего времени наработки до отказа; расчет среднего времени наработки до отказа за все время моделирования работы системы; расчет вероятности отказа ПО в единицу расчёт коэффициента готовности Таким образом, наша ...
... , что каждый из них можно представить как шкалу в многомерном фазовом пространстве, тогда конкретным АСУ в этом пространстве будут соответствовать точки или определенные области. 2.2. Классификация систем и автоматизация управления сложными системами Прежде всего система – это целостная совокупность некоторых элементов, не сводящаяся к простой сумме своих частей, т.е. представляющая собой ...
... разных этапах производства (потребления) электроэнергии. Основная цель создания таких систем – дальнейшеё повышение эффективности технических и программных средств автоматизации и диспетчеризации СЭС для улучшения технико-экономических показателей и повышения качества и надёжности электроснабжения ПП. Реформирование электроэнергетики России требует создания полномасштабных иерархических систем ...
... , повысить вероятность выявления дефектов и, с другой стороны, снизить различные технико-экономические затраты на проведение контроля. 2. Проектирование системы контроля знаний 2.1 Общая структура системы По своей логической структуре система состоит из трёх частей: - подсистемы конфигурирования теста; - подсистемы тестирования; - подсистема сервиса. ...


0 комментариев