Математические модели надёжности комплексов программ

3.6 Математические модели надёжности комплексов программ

Математические модели позволяют оценивать характеристики ошибок в программах и прогнозировать их надёжность при проектировании и эксплуатации. Модели имеют вероятностный характер, и достоверность прогнозов зависит от точности исходных данных и глубины прогнозирования по времени. Эти математические модели предназначены для оценки:

- показателей надёжности комплексов программ в процессе отладки;

- количества ошибок, оставшихся невыявленными;

- времени, необходимого для обнаружения следующей ошибки в функционирующей программе;

- времени, необходимого для выявления всех ошибок с заданной вероятностью.

Использование моделей позволяет эффективно и целеустремлённо проводить отладку и испытания комплексов программ, помогает принять рациональное решение о времени прекращения отладочных работ.

В настоящее время предложен ряд математических моделей, основными из которых являются:

- экспоненциальная модель изменения ошибок в зависимости от времени отладки;

- модель, учитывающая дискретно - понижающуюся частоту появления ошибок как линейную функцию времени тестирования и испытаний;

- модель, базирующаяся на распределении Вейбула;

- модель, основанная на дискретном гипергеометрическом распределении.

При обосновании математических моделей выдвигаются некоторые гипотезы о характере проявления ошибок в комплексе программ. Наиболее обоснованными представляются предположения, на которых базируется первая экспоненциальная модель изменения ошибок в процессе отладки и которые заключаются в следующем:

1. Любые ошибки в программе являются независимыми и проявляются в случайные моменты времени.

2. Время работы между ошибками определяется средним временем выполнения команды на данной ЭВМ и средним числом команд, исполняемым между ошибками. Это означает, что интенсивность проявления ошибок при реальном функционировании программы зависит от среднего быстродействия ЭВМ.

3. Выбор отладочных тестов должен быть представительным и случайным, с тем чтобы исключить концентрацию необнаруженных ошибок для некоторых реальных условий функционирования программы.

4. Ошибка, являющаяся причиной искажения результатов, фиксируется и исправляется после завершения тестирования либо вообще не обнаруживается.

Из этих свойств следует, что при нормальных условиях эксплуатации количество ошибок, проявляющихся в некотором интервале времени, распределено по закону Пуассона. В результате длительность непрерывной работы между искажениями распределена экспоненциально.

Предположим, что в начале отладки комплекса программ при t = 0 в нём содержалось ошибок. После отладки в течении времени t осталось ошибок и устранено n ошибок (+ n = ). При этом время t соответствует длительности исполнения программ на вычислительной системе (ВС) для обнаружения ошибок и не учитывает простои машины, необходимые для анализа результатов и проведения корректировок.

Интенсивность обнаружения ошибок в программе dn/dt и абсолютное количество устранённых ошибок связываются уравнением

 (3.13)

где k - коэффициент.

Если предположить, что в начале отладки при t = 0 отсутствуют обнаруженные ошибки, то решение уранения (3.13) имеет вид

 (3.14)

Количество оставшихся ошибок в комплексе программ

пропорционально интенсивности обнаружения dn/dt с точностью до коэффициента k.

Время безотказной работы программ до отказа T или наработка на отказ, который рассматривается как обнаруживаемое искажение программ, данных или вычислительного процесса, нарушающее работоспособность, равно величине, обратной интенсивности обнаружения отказов (ошибок):

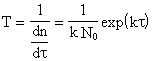 (3.15)

Если учесть, что до начала тестирования в комплексе программ содержалось ошибок и этому соответствовала наработка на отказ , то функцию наработки на отказ от длительности проверок можно представить в следующем виде:

 (3.16)

Если известны моменты обнаружения ошибок  и каждый раз в эти моменты обнаруживается и достоверно устраняется одна ошибка, то, используя метод максимального правдоподобия, можно получить уравнение для определения значения начального числа ошибок :

 (3.17)

а также выражение для расчёта коэффициента пропорциональности

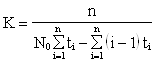 ; (3.18)

В результате можно рассчитать число оставшихся в программе ошибок и среднюю наработку на отказ Tср = 1/l , т.е. получить оценку времени до обнаружения следующей ошибки.

В процессе отладки и испытаний программ для повышения наработки на отказ от до  необходимо обнаружить и устранить Dn ошибок. Величина Dn определяется соотношением:

; (3.19)

Выражение для определения затрат времени Dt на проведение отладки, которые позволяют устранить Dn ошибок и соответственно повысить наработку на отказ от значения до, имеет вид:

 (3.20)

Вторая модель построена на основе гипотезы о том, что частота проявления ошибок (интенсивность отказов) линейно зависит от времени испытания  между моментами обнаружения последовательных i - й и (i - 1) - й ошибок.

, (3.21)

где - начальное количество ошибок; K - коэффициент пропорциональности, обеспечивающий равенство единице площади под кривой вероятности обнаружения ошибок.

Для оценки наработки на отказ получается выражение, соответствующее распределению Релея:

 (3.22)

где .

Отсюда плотность распределения времени наработки на отказ

. (3.23)

Использовав функцию максимального правдоподобия, получим оценку для общего количества ошибок и коэффициента K.

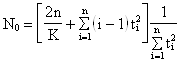 (3.24)

 (3.25)

Особенностью третьей модели является учёт ступенчатого характера изменения надёжности при устранении очередной ошибки. В качестве основной функции рассматривается распределение времени наработки на отказ P(t). Если ошибки не устраняются, то интенсивность отказов является постоянной, что приводит к экспоненциальной модели для распределения:

Отсюда плотность распределения наработки на отказ T определяется выражением:

где t > 0, l > 0 и 1/l - среднее время наработки на отказ, т.е. Тср=1/l. Здесь Тср - среднее время наработки на отказ.

Для аппроксимации изменения интенсивности от времени при обнаружении и устранении ошибок используется функция следующего вида:

;

Если 0 < b < 1, то интенсивность отказов снижается по мере отладки или в процессе эксплуатации. При таком виде функции l(t) плотность функции распределения наработки на отказ описывается двухпараметрическим распределением Вейбулла:

.

Распределение Вейбулла достаточно хорошо отражает реальные зависимости при расчёте функции наработки на отказ.

3.7 Проверка математических моделей

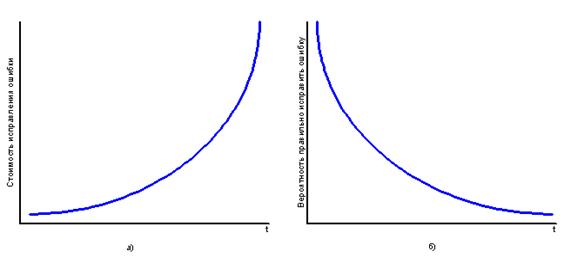
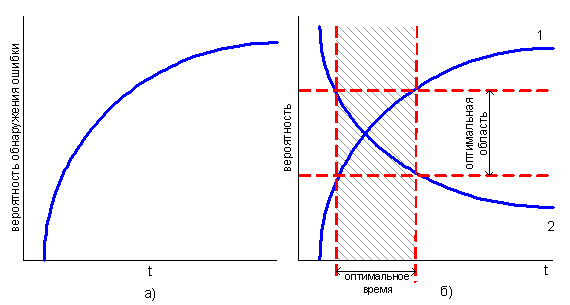
Обоснование приведённых математических моделей приведено в ряде работ, в которых наибольшее внимание уделялось проверке первой и второй моделей. Контролировались и обрабатывались экспериментальные данные интенсивности обнаружения ошибок dn/dt на фиксированном интервале времени, количества обнаруженных ошибок n или наработки на отказ T в зависимости от времени функционирования программ на вычислительной системе. Характеристики, полученные расчётами с использованием математических моделей, сопоставлялись с полученными экспериментальными значениями и применялись для прогнозирования показателей с последующим анализом отклонений от экспериментальных данных.

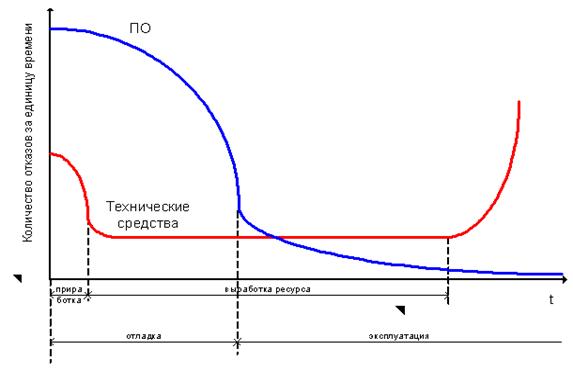
Пример анализа первой модели приведён на рис. 3.3. Определялся и прогнозировался интервал времени между последовательными отказами при непрерывном

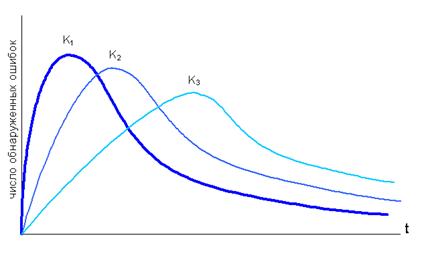
Для оценки достоверности моделей анализировалось количество ошибок n, выявленное при функционировании комплексов программ в течении времени t [см. (3.14)]. Значения и K определялись методом максимального правдоподобия для каждого из 16 исследованных вариантов создания больших программ. Пример изменения количества выявленных ошибок в зависимости от времени функционирования одного комплекса программ представлен на рис. 3.4. Из графика следует, что первая модель [см. (3.14)] хорошо аппроксимирует количество ошибок во всём исследованном интервале времени. При значениях n > 288 отклонение реального количества обнаруженных ошибок от расчётного составляет 21%.

ЛИТЕРАТУРА

1. Надёжность автоматизированных систем управления. / Под редакцией Я.А. Хетагурова.- М.: Высшая школа, 1979 - 287с.

2. Половко А.М. Основы теории надёжности. - М.: Наука, 1964 - 446с.

3. Голинкевич Т.А. Прикладная теория надёжности. - М.: Высшая школа, 1985 - 168с.

4. Маликов И.М. Надёжность судовой электронной аппаратуры и систем автоматического управления. - Л.: Судостроение, 1967 - 315с.

5. Шишонок Н.А. и др.Основы теории надёжности и эксплуатации радиоэлектронной техники. - М.: Советское радио, 1964 - 551с.

6. Шор Я.Б. Статистические методы анализа и контроля качества и надёжности. - М.: Советское радио, 1962 - 552с.

7. Росин М.Ф., Булыгин В.С. Статистическая динамика и теория эффективности систем управления. - М.: Машиностроение, 1981 - 312с.

8. Вероятностные методы в вычислительной технике. - М.: Высшая школа, 1986 - 312с.

9. Яншин А.А. Теоретические основы конструирования, технологии и надёжности ЭВА. - М.: Радио и связь, 1983 - 312с.

10. Рудзит Я.А., Плуталов В.Н. Основы метрологии, точность и надёжность в приборостроении. - М.: Машиностроение, 1991 - 303с.

11. Саяпин В.В. Конспект лекций по курсу “Основы теории надёжности”. - М.: МВ и ССО СССР, МАИ, 1971 - 142с.

12. Дружинин Г.В. Надёжность автоматизированных производственных систем. - М.: Энергоатомиздат, 1986 - 479с.

13. Липаев В.В. Надёжность программного обеспечения АСУ. - М.: Энергоиздат, 1981 - 240с.

14. Шураков В.В. Надёжность программного обеспечения систем обработки данных. - М.: Финансы и статистика, 1987 - 271с.

15. Садчиков П.И., Приходько Ю.Г. Методы оценки надёжности и обеспечения устойчивости функционирования программ. - М.: Знание, 1983 - 102с.

16. Сборник задач по теории надёжности./ Под редакцией А.М. Половко и И.М. Маликова. - М.: Советское радио, 1972 - 407с.

17. Теория надёжности радиоэлектронных схем в примерах и задачах. - М.: Энергия, 1976 - 448с.

18. Снегирёв А.А. Сборник задач по надёжности САУ. - М.: МВ и ССО СССР, МИФИ, 1978 - 87с.

19. Тейер Т., Липов М., Нельсон Э. Надёжность программного обеспечения. - М.: Мир, 1981 - 325с.

20. Майерс Г. Надёжность программного обеспечения. - М.: Мир, 1980 - 360с.

21. Гласс Р. Руководство по надёжному программированию. - М.: Финансы и статистика, 1982 - 256с.

Похожие работы

Разработка программно–алгоритмических средств для определения надёжности программного обеспечения на основании моделирования работы системы типа "клиент–сервер"

Скачать

104437

5

35

... первоначальное количество ошибок можно оценить как: Поставленная задача позволяет определить такие важные характеристики функционирования программного комплекса, как: расчет текущего времени наработки до отказа; расчет среднего времени наработки до отказа за все время моделирования работы системы; расчет вероятности отказа ПО в единицу расчёт коэффициента готовности Таким образом, наша ...

Классификация автоматизированных систем управления

Скачать

22140

0

0

... , что каждый из них можно представить как шкалу в многомерном фазовом пространстве, тогда конкретным АСУ в этом пространстве будут соответствовать точки или определенные области.   2.2. Классификация систем и автоматизация управления сложными системами Прежде всего система – это целостная совокупность некоторых элементов, не сводящаяся к простой сумме своих частей, т.е. представляющая собой ...

Автоматизация и диспетчеризация систем электроснабжения

Скачать

129027

5

16

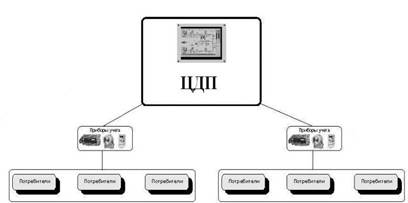
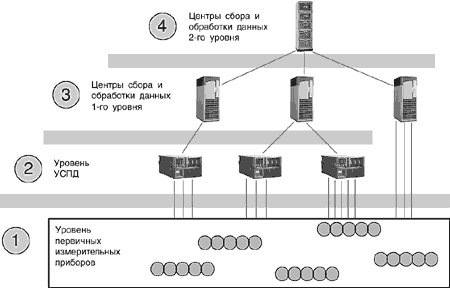
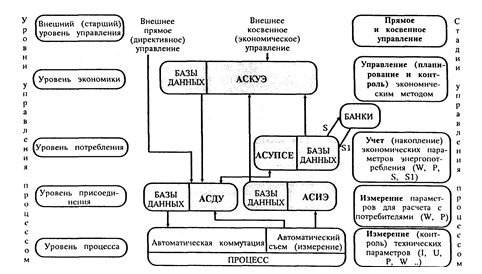
... разных этапах производства (потребления) электроэнергии. Основная цель создания таких систем – дальнейшеё повышение эффективности технических и программных средств автоматизации и диспетчеризации СЭС для улучшения технико-экономических показателей и повышения качества и надёжности электроснабжения ПП. Реформирование электроэнергетики России требует создания полномасштабных иерархических систем ...

Автоматизированная система контроля знаний специалистов по дефектоскопии

Скачать

131566

7

26

... , повысить вероятность выявления дефектов и, с другой стороны, снизить различные технико-экономические затраты на проведение контроля. 2. Проектирование системы контроля знаний 2.1 Общая структура системы По своей логической структуре система состоит из трёх частей: -            подсистемы конфигурирования теста; -            подсистемы тестирования; -            подсистема сервиса. ...