НАДЁЖНОСТЬ НЕРЕМОНТИРУЕМЫХ ИЗДЕЛИЙ
Виды надёжности
Теорема сложения вероятностей
Плотность вероятности f(t) времени безотказной работы T
Числовые характеристики надёжности
Экспериментальная оценка надёжности изделий
Критерий Пирсона
Законы распределения отказов и их основные характеристики
Закон распределения Вейбулла
Виды соединения элементов в систему
Параллельное соединение элементов в систему
Расчёт надёжности системы с постоянным общим резервированием
Режим нагруженного резерва
НАДЁЖНОСТЬ РЕМОНТИРУЕМЫХ (ВОССТАНАВЛИВАЕМЫХ) ИЗДЕЛИЙ
НАДЁЖНОСТЬ ПРОГРАММНОГО ОБЕСПЕЧЕНИЯ
Математические модели надёжности комплексов программ
Навигация
НАДЁЖНОСТЬ РЕМОНТИРУЕМЫХ (ВОССТАНАВЛИВАЕМЫХ) ИЗДЕЛИЙ
Надёжность функционирования автоматизированных систем
89220
знаков
0
таблиц
3
изображения
2. НАДЁЖНОСТЬ РЕМОНТИРУЕМЫХ (ВОССТАНАВЛИВАЕМЫХ) ИЗДЕЛИЙ
2.1 Надёжность системы с восстановлением
Восстанавливаемую систему целесообразно рассматривать как систему массового обслуживания, в которой поток заявок на обслуживание представляет собой поток отказов аппаратуры. Каналами обслуживания являются ремонтные бригады, восстанавливающие работоспособность аппаратуры.
Будем считать, что поток заявок на обслуживание - пуассоновский.
Поток восстановлений - также пуассоновский.
В этом случае для анализа надёжности восстанавливаемой системы можно использовать теорию марковских случайных процессов.
Имеем нерезервированную восстанавливаемую систему, состоящую из одного элемента. Система находится под действием пуассоновского потока отказов с интенсивностью l. После отказа система начинает немедленно восстанавливаться (ремонтироваться). Поток восстановлений - пуассоновский с интенсивностью m.
В любой момент времени система может находиться в одном из двух состояний:
- состояние работоспособности,
- состояние отказа (ремонта),
- вероятность нахождения системы в состоянии ,
- вероятность нахождения системы в состоянии .
Требуется определить функцию готовности 
и функцию простоя 
нерезервированной восстанавливаемой системы.
Функция готовности совпадает с вероятностью работоспособного состояния , т.е.
=.
Функция простоя совпадает с вероятностью отказа, т.е.
= .
Составим систему дифференциальных уравнений Колмогорова. Имеем
(2.1)
Предположим, что при t = 0 система находилась в работоспособном состоянии , т.е.
Для любого момента времени t имеем
(2.2)
Из двух уравнений (2.1) одно является лишним, т.к. 
и 
связаны соотношением (2.2). Учитывая это, отбросим второе уравнение, а в первое уравнение вместо подставим 1 - . Имеем:
или 
(2.3)
Будем искать решение уравнения при ненулевых начальных условиях.
Запишем решение уравнения (2.3). Имеем:
или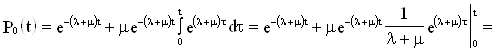 
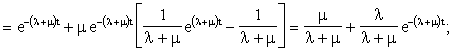
Таким образом
Определим . Имеем: 
Таким образом:
При длительной эксплуатации, т.е. при t ® ¥ имеем:
где 
- коэфициент готовности системы, 
- коэфициент простоя системы.
Учитывая, что
, 
.
где 
- среднее время безотказной работы системы;
- среднее время восстановления (ремонта) системы,
имеем
; 
;
, 
;
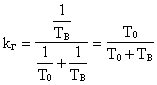Таким образом, коэффициент готовности характеризует долю времени, в течении которого система работоспособна. Коэффициент простоя характеризует долю времени, в течении которого система ремонтируется.
Определим коэффициент готовности и коэффициент простоя системы, содержащей основной и n - 1 резервных элементов, находящихся в нагруженном режиме. Отказавшие элементы образуют очередь на ремонт, который осуществляется одной бригадой с интенсивностью m. Интенсивность отказа любого элемента равна l.
Введём в рассмотрение состояния , , ………., 
:
- работоспособны все n элементов
- отказал один элемент, остальные работоспособны
- отказали два элемента, остальные исправны
- отказали i элементов, остальные исправны
…………………………………………………….
- отказала вся система, т.е. отказали все n элементов.
Построим граф состояния системы.
Составим систему дифференциальных уравнений Колмогорова. Имеем:
……………………………………….
где 
- вероятность нахождения системы в момент времени t в состоянии , i = 0,1…, n
В установившемся режиме имеем:
;
;
В результате получим систему алгебраических уравнений вида:
Из системы алгебраических уравнений имеем:
Для вероятностей состояний справедливо следующее соотношение
;
Определим 
. Имеем:
.
;
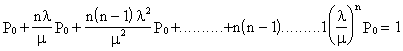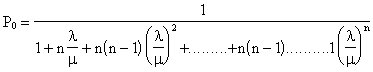или 
Отсюда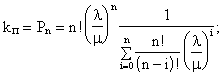 
Коэффициент готовности:
Похожие работы
... первоначальное количество ошибок можно оценить как: Поставленная задача позволяет определить такие важные характеристики функционирования программного комплекса, как: расчет текущего времени наработки до отказа; расчет среднего времени наработки до отказа за все время моделирования работы системы; расчет вероятности отказа ПО в единицу расчёт коэффициента готовности Таким образом, наша ...
... , что каждый из них можно представить как шкалу в многомерном фазовом пространстве, тогда конкретным АСУ в этом пространстве будут соответствовать точки или определенные области. 2.2. Классификация систем и автоматизация управления сложными системами Прежде всего система – это целостная совокупность некоторых элементов, не сводящаяся к простой сумме своих частей, т.е. представляющая собой ...
... разных этапах производства (потребления) электроэнергии. Основная цель создания таких систем – дальнейшеё повышение эффективности технических и программных средств автоматизации и диспетчеризации СЭС для улучшения технико-экономических показателей и повышения качества и надёжности электроснабжения ПП. Реформирование электроэнергетики России требует создания полномасштабных иерархических систем ...
... , повысить вероятность выявления дефектов и, с другой стороны, снизить различные технико-экономические затраты на проведение контроля. 2. Проектирование системы контроля знаний 2.1 Общая структура системы По своей логической структуре система состоит из трёх частей: - подсистемы конфигурирования теста; - подсистемы тестирования; - подсистема сервиса. ...
0 комментариев