Числовые характеристики надёжности

1.10 Числовые характеристики надёжности

Рассмотренные количественные характеристики надёжности являются функциями времени. Для определения этих характеристик на основе опытных данных с достаточной точностью требуется большой объём испытаний. Более просто найти числовые характеристики надёжности. К ним относятся:

1) среднее время безотказной работы;

2) дисперсия времени безотказной работы;

Определим среднее время безотказной работы или математическое ожидание случайной величины T. Имеем

Величина  также называется средняя наработка на отказ.

Известно, что f(t) = . Тогда:

.

Этот интеграл можно вычислить по частям

;

u = t; ;

du = dt; v = P(t) ;

;

т.к. P(t) при t ® ¥ убывает быстрее, чем растёт t.

Для экспоненциального закона надёжности имеем:

;

.

Итак, для экспоненциального закона надёжности среднее время безотказной работы есть величина, обратная интенсивности отказов.

Приближённое значение  можно определить по формуле , где  

Здесь - время безотказной работы i - го изделия; N - общее число изделий, поставленных на испытания.

Определим дисперсию времени безотказной работы. Имеем

;

.

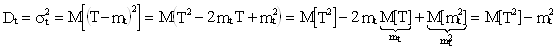Интеграл берём по частям

; ;

; v = P(t) ;

;

Для экспоненциального закона надёжности имеем:

; ;

.

Интеграл берём по частям:

u = t ; ;

du = dt; ;

;

; ;

Дисперсия  характеризует степень разброса значений T относительно .

На основании результатов испытаний можно определить приближённое значение дисперсии

;

где .

1.11 Характеристики ремонтопригодности

Рассмотрим систему длительного (многократного) использования. В этом случае система после отказа восстанавливается и затем продолжает функционировать.

Время восстановления системы - суммарное время обнаружения и устранения отказов.

 зависит от многих факторов, имеющих случайный характер (вид отказа, тип и число отказавших элементов).

- случайная величина.

Ремонтопригодность системы характеризуется следующими вероятностными характеристиками:

1) вероятность выполнения ремонта в заданное время ;

2) вероятность невыполнения ремонта в заданное время ;

3) плотность вероятности времени восстановления ;

4) интенсивность восстановления ;

5) среднее время восстановления ;

6) дисперсия времени восстановления .

Вероятность выполнения ремонта в заданное время - это вероятность того, что отказ изделия будет устранён в течении заданного t

.

Вероятность невыполнения ремонта в заданное время - это вероятность того, что отказ изделия не будет устранён в течении заданного времени t

.

Плотность вероятности времени восстановления равна

.

Событие А - отказ изделия не устранён на интервале времени от 0 до t.

Событие В - отказ изделия не устранён на интервале времени от до .

АВ - произведение событий А и В. Произведением событий А и В является событие, заключающееся в совместном появлении этих событий

P(AB) = P(A) P(B/A).

P(B/A) - условная вероятность события В при условии, что событие А произошло (имело место).

- вероятность того, что отказ изделия не устранён на интервале времени от 0 до t.

P(B/A) = P(AB) / P(A).

Вероятность P(AB) есть вероятность того, что отказ изделия не устранён на интервале

т.е. P(AB) =  

- вероятность того, что отказ изделия не устранён на интервале времени  при условии, что отказ изделия не был устранён на интервале времени от 0 до t.

Таким образом

 ;

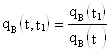- вероятность того, что отказ изделия будет устранён на интервале времени при условии, что отказ изделия не был устранён на интервале времени от 0 до t.

.

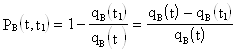Пусть ; тогда

 ;

 ;

;

.

Таким образом: ; (*)

 или:  

Из (*) имеем ;

или ;

или ;

;

 вероятность выполнения ремонта в заданное время.

При  получаем экспоненциальный закон ремонтопригодности

Определим среднее время восстановления :

;

;

;

Это интеграл можно вычислить по частям

u = t; ;

du = dt; ;

;

;

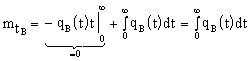-дисперсия времени восстановления

В случае экспоненциального закона ремонтопригодности имеем:

; .

Похожие работы

Разработка программно–алгоритмических средств для определения надёжности программного обеспечения на основании моделирования работы системы типа "клиент–сервер"

Скачать

104437

5

35

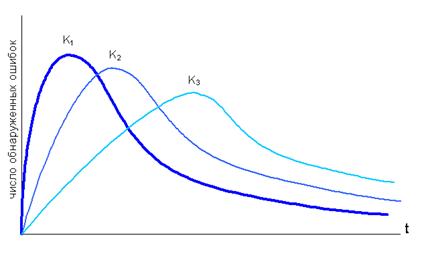
... первоначальное количество ошибок можно оценить как: Поставленная задача позволяет определить такие важные характеристики функционирования программного комплекса, как: расчет текущего времени наработки до отказа; расчет среднего времени наработки до отказа за все время моделирования работы системы; расчет вероятности отказа ПО в единицу расчёт коэффициента готовности Таким образом, наша ...

Классификация автоматизированных систем управления

Скачать

22140

0

0

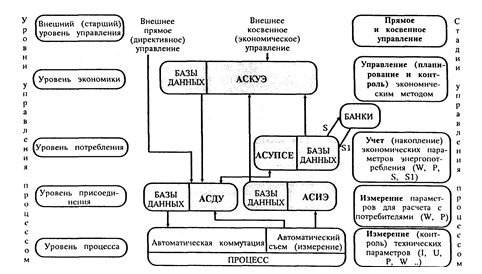
... , что каждый из них можно представить как шкалу в многомерном фазовом пространстве, тогда конкретным АСУ в этом пространстве будут соответствовать точки или определенные области.   2.2. Классификация систем и автоматизация управления сложными системами Прежде всего система – это целостная совокупность некоторых элементов, не сводящаяся к простой сумме своих частей, т.е. представляющая собой ...

Автоматизация и диспетчеризация систем электроснабжения

Скачать

129027

5

16

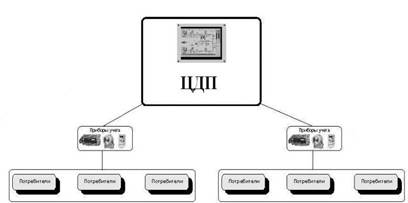
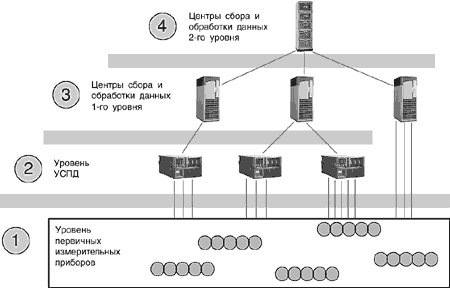
... разных этапах производства (потребления) электроэнергии. Основная цель создания таких систем – дальнейшеё повышение эффективности технических и программных средств автоматизации и диспетчеризации СЭС для улучшения технико-экономических показателей и повышения качества и надёжности электроснабжения ПП. Реформирование электроэнергетики России требует создания полномасштабных иерархических систем ...

Автоматизированная система контроля знаний специалистов по дефектоскопии

Скачать

131566

7

26

... , повысить вероятность выявления дефектов и, с другой стороны, снизить различные технико-экономические затраты на проведение контроля. 2. Проектирование системы контроля знаний 2.1 Общая структура системы По своей логической структуре система состоит из трёх частей: -            подсистемы конфигурирования теста; -            подсистемы тестирования; -            подсистема сервиса. ...