НАДЁЖНОСТЬ НЕРЕМОНТИРУЕМЫХ ИЗДЕЛИЙ
Виды надёжности
Теорема сложения вероятностей
Плотность вероятности f(t) времени безотказной работы T
Числовые характеристики надёжности
Экспериментальная оценка надёжности изделий
Критерий Пирсона
Законы распределения отказов и их основные характеристики
Закон распределения Вейбулла
Виды соединения элементов в систему
Параллельное соединение элементов в систему
Расчёт надёжности системы с постоянным общим резервированием
Режим нагруженного резерва
НАДЁЖНОСТЬ РЕМОНТИРУЕМЫХ (ВОССТАНАВЛИВАЕМЫХ) ИЗДЕЛИЙ
НАДЁЖНОСТЬ ПРОГРАММНОГО ОБЕСПЕЧЕНИЯ
Математические модели надёжности комплексов программ
Навигация
Теорема сложения вероятностей
Надёжность функционирования автоматизированных систем
89220
знаков
0
таблиц
3
изображения
1.6.2 Теорема сложения вероятностей
Вероятность суммы n несовместных событий равна сумме вероятностей этих событий
.
Сумма вероятностей n несовместных событий, образующих полную группу событий, равна единице
;
где 
- несовместные события, образующие полную группу.
Следствие: Сумма вероятностей двух противоположных событий равна единице
.
1.6.3 Теорема умножения вероятностей
Зависимое событие - это такое событие, вероятность которого зависит от того, произошли или не произошли остальные события.
Независимое событие - это такое событие, вероятность которого не зависит от того, произошли или не произошли остальные события.
Вероятность произведения n независимых событий равна произведению вероятностей этих событий
.
Условная вероятность 
:
- условная вероятность события А при условии, что событие В имело место.
Вероятность произведения двух событий равна произведению вероятности 1-го события на условную вероятность 2-го события, при условии, что 1-ое событие имело место:
.
1.6.4 Теорема полной вероятности
Пусть требуется определить вероятность некоторого события А, которое может произойти вместе с одним из событий
События образуют полную группу n несовместных событий. Будем называть эти события гипотезами.
Вероятность события А определяется формулой
- формула полной вероятности.
где 
- вероятность осуществления гипотезы 
;
- условная вероятность события А при условии, что событие имело место.
1.7 Количественные характеристики надёжности.
Предварительно рассмотрим понятие “случайная величина”.
Случайная величина - величина, которая в результате опыта может принять то или иное значение, причём заранее неизвестно, какое именно.
Примеры случайной величины:
1) Интервал времени между соседними отказами ЭВМ;
2) Интервал времени от начала работы изделия до первого отказа или время безотказной работы;
3) Число деталей, изготовленных рабочим в единицу времени.
Обозначим через T - время безотказной работы изделия (интервал времени от начала работы изделия до первого отказа). T - случайная величина. Величина T также называется наработка на отказ изделия. t - возможные значения случайной величины T.
Введём понятие “вероятность безотказной работы”.
- вероятность того, что время безотказной работы изделия будет больше или равно некоторому значению t. Другими словами, вероятностью безотказной работы называется вероятность того, что при заданных условиях эксплуатации в течении интервала времени t не возникнет отказа, т.е.система будет работоспособна.
Вероятность отказа:
- вероятность того, что время безотказной работы изделия меньше некоторого заданного значения t.
Другими словами, вероятностью отказа является вероятность того, что в течении заданного времени произойдёт хотя бы один отказ.
Функция представляет собой функцию распределения случайной величины Т.
События В и С несовместные события (в опыте не могут появиться вместе).
А = В + С; P(A) = P(B) + P(С);
откуда
P(С) = P(A) - P(B); P(A) = 
; P(B) = 
;
P(C) = 
;
Следовательно
= - ;
или
= 
- 
;
Введём в рассмотрение событие А. Событие А означает, что 
, т.е. в интервале времени от 0 до t отказа не произойдёт.
Введём в рассмотрение событие 
. Событие означает, что T < t , т.е в интервале времени от 0 до t произойдёт отказ. События A и являются противоположными, т.к. они образуют полную группу событий. События образуют полную группу, если в результате опыта одно из них обязательно должно произойти.
Из теории вероятностей известно, что сумма вероятностей противоположных событий равна единице, т.е.
P(A) + P
;
P(A) = P(T ³ t) ; P
= P(T<t) ;
Следовательно
P(T ³ t) + P(T < t) = 1 или
P(t) + q(t) = 1
Для вероятности безотказной работы справедливо приближённое соотношение
P(t) »
, где = 
Здесь n(t) - число изделий, не отказавших к моменту времени t;
N - Число изделий, поставленных на испытания.
Испытания изделий должны проводиться при одинаковых условиях так, чтобы отказы изделий были независимы друг от друга.
Для вероятности отказа справедливо приближённое равенство
; где 
.
Здесь N - n(t) - число изделий, отказавших к моменту времени t.
Похожие работы
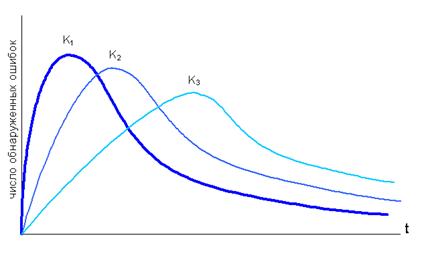
... первоначальное количество ошибок можно оценить как: Поставленная задача позволяет определить такие важные характеристики функционирования программного комплекса, как: расчет текущего времени наработки до отказа; расчет среднего времени наработки до отказа за все время моделирования работы системы; расчет вероятности отказа ПО в единицу расчёт коэффициента готовности Таким образом, наша ...
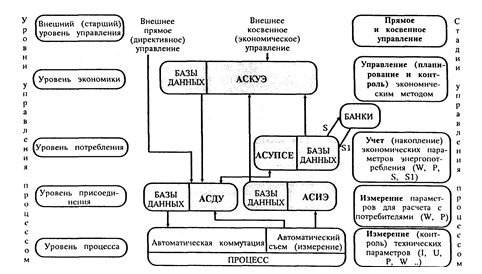
... , что каждый из них можно представить как шкалу в многомерном фазовом пространстве, тогда конкретным АСУ в этом пространстве будут соответствовать точки или определенные области. 2.2. Классификация систем и автоматизация управления сложными системами Прежде всего система – это целостная совокупность некоторых элементов, не сводящаяся к простой сумме своих частей, т.е. представляющая собой ...
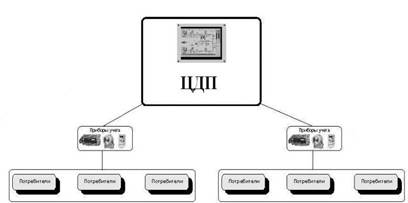
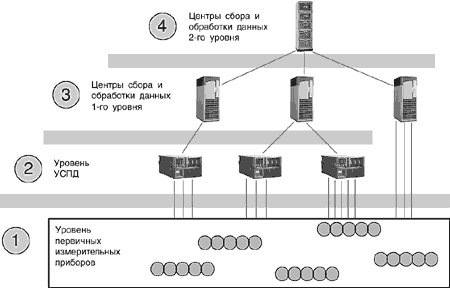
... разных этапах производства (потребления) электроэнергии. Основная цель создания таких систем – дальнейшеё повышение эффективности технических и программных средств автоматизации и диспетчеризации СЭС для улучшения технико-экономических показателей и повышения качества и надёжности электроснабжения ПП. Реформирование электроэнергетики России требует создания полномасштабных иерархических систем ...
... , повысить вероятность выявления дефектов и, с другой стороны, снизить различные технико-экономические затраты на проведение контроля. 2. Проектирование системы контроля знаний 2.1 Общая структура системы По своей логической структуре система состоит из трёх частей: - подсистемы конфигурирования теста; - подсистемы тестирования; - подсистема сервиса. ...
0 комментариев